Задачи по начертательной геометрии

 

К задачам, номер которых отмечены надстрочной звездочкой, необходимо по­строить алгоритмы в блок-схемной форме и чертежи (эпюры) с использованием мнемо­нических знаков, указывающих последова­тельность выполнения элементарных графи­ческих процедур, и отметить минимальное число этих процедур.

Таблица I

 

 

 

- 46 -

Задачи (см. текст и чертежи к ним) предназначены для самостоятельного реше­ния студентами в процессе изучения ими курса перед выполнением контрольных ра­бот и для подготовки к экзаменам.

Все построения выполняются каранда­шом с применением чертежных инструмен­тов Линии построения, необходимые для решения каждой задачи, следует сохранить на чертеже. Допускается применение цвет­ных карандашей В задачах, в которых есть текстовое условие, но нет графического со­провождения, чертеж выполнить самостоя­тельно (придумать). Заданное графическое условие увеличивайте в 1,5…2 раза. Для лучшего понимания чертежей обозначайте характерные точки Решать задачи легче в тетради в клеточку.

 

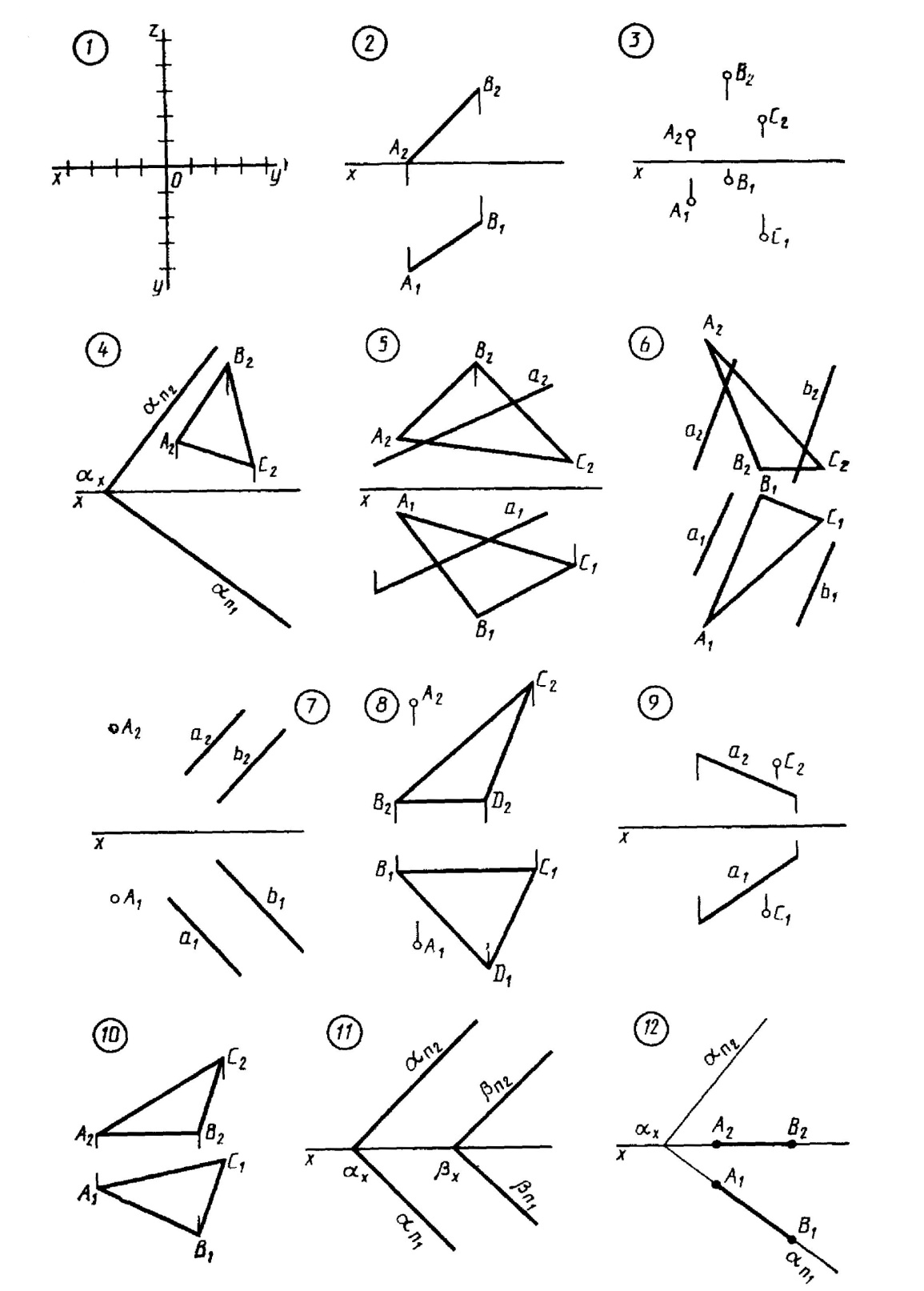
К темам 2 и 3. Точка, прямая, плос­кость, позиционные и метрические задачи.

1. Построить проекции точек А, В и С по координатам- А(2, I, 3), В(3, 3, 4), С(5, 4, 2) Первой дана координата X, второй – У, третьей – Z.

Таблица II

 

- 47 -

2*. Определить длину отрезка прямой а(А, В) и построить фронтальный и гори­зонтальный следы прямой а(А, В).

3. Построить фронтальный и горизон­тальный следы плоскости а, заданной точ­ками А, В и С, не лежащими на одной пря­мой.

4. Построить горизонтальную проекцию треугольника ABC, принадлежащего плос­кости а, и определить углы q и ψ наклона плоскости а соответственно к плоскостям проекций П₁ и П₂

 

Таблица III

5*. Определить точку пересечения пря­мой а с плоскостью α (А, В, С).

- 48 -

6. Построить линию пересечения плоско­сти α (А, В, С) с плоскостью β(a // b).

7*. Через точку А провести плоскость, параллельную плоскости В (a // b´), задав ее пересекающимися прямыми.

8*. Определить расстояние от точки А до плоскости α (В, С, D) (без преобразо­вания проекций).

9. Провести через точку С плоскость α, перпендикулярную прямой а. Задать плос­кость пересекающимися прямыми.

 

Таблица IV

 

К теме 4. Способы преобразования проекций.

10. Способом вращения вокруг осей, пер­пендикулярных плоскостям проекций, опре­делить величину треугольника ABC.

11 Способом замены плоскостей проек­ции определить расстояние между парал­лельными плоскостями аир.

- 49 -

12. Способом совмещения плоскости с одной из плоскостей проекций построить проекции равностороннего треугольника ABC, принадлежащего плоскости а, по его стороне АВ.

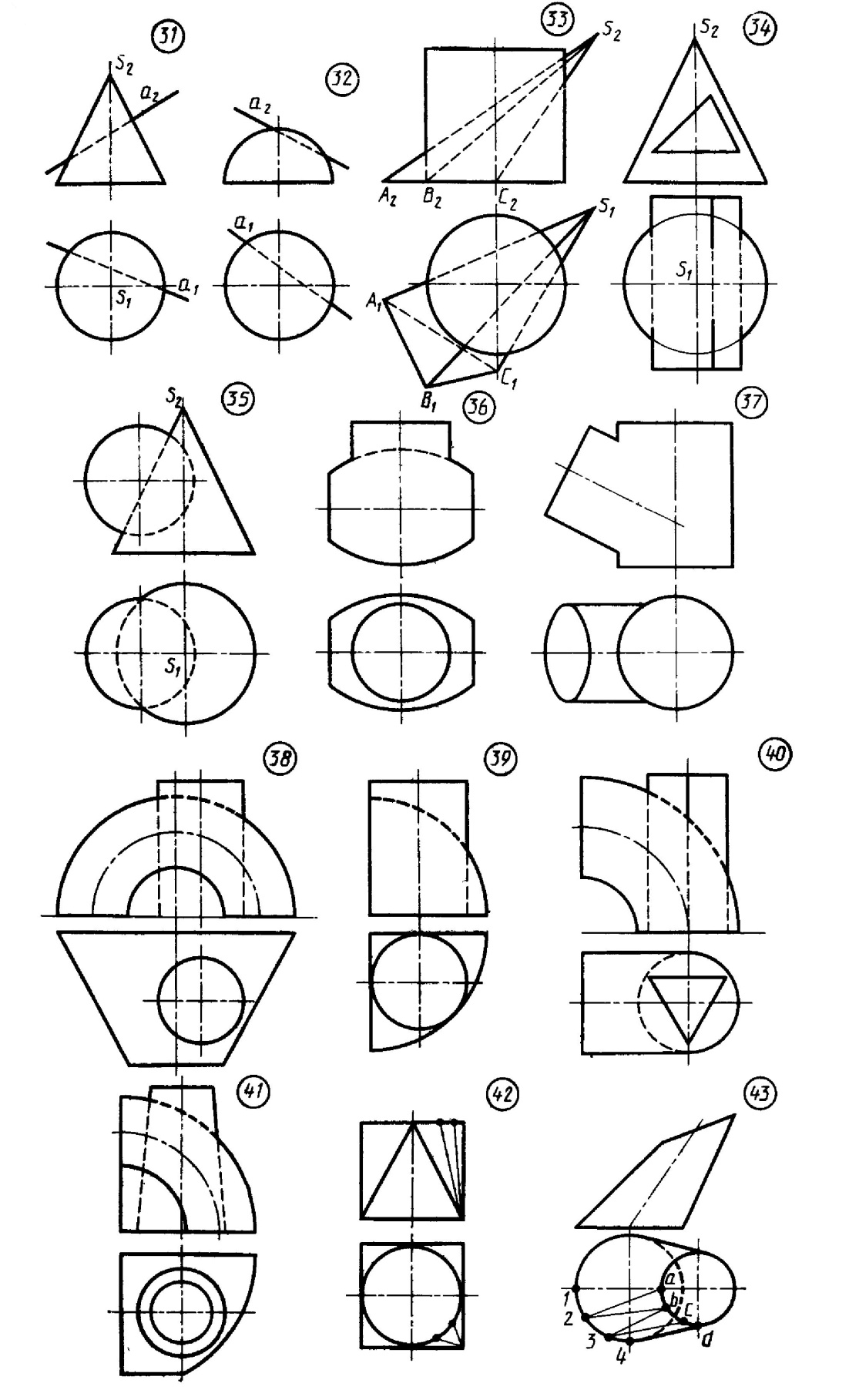
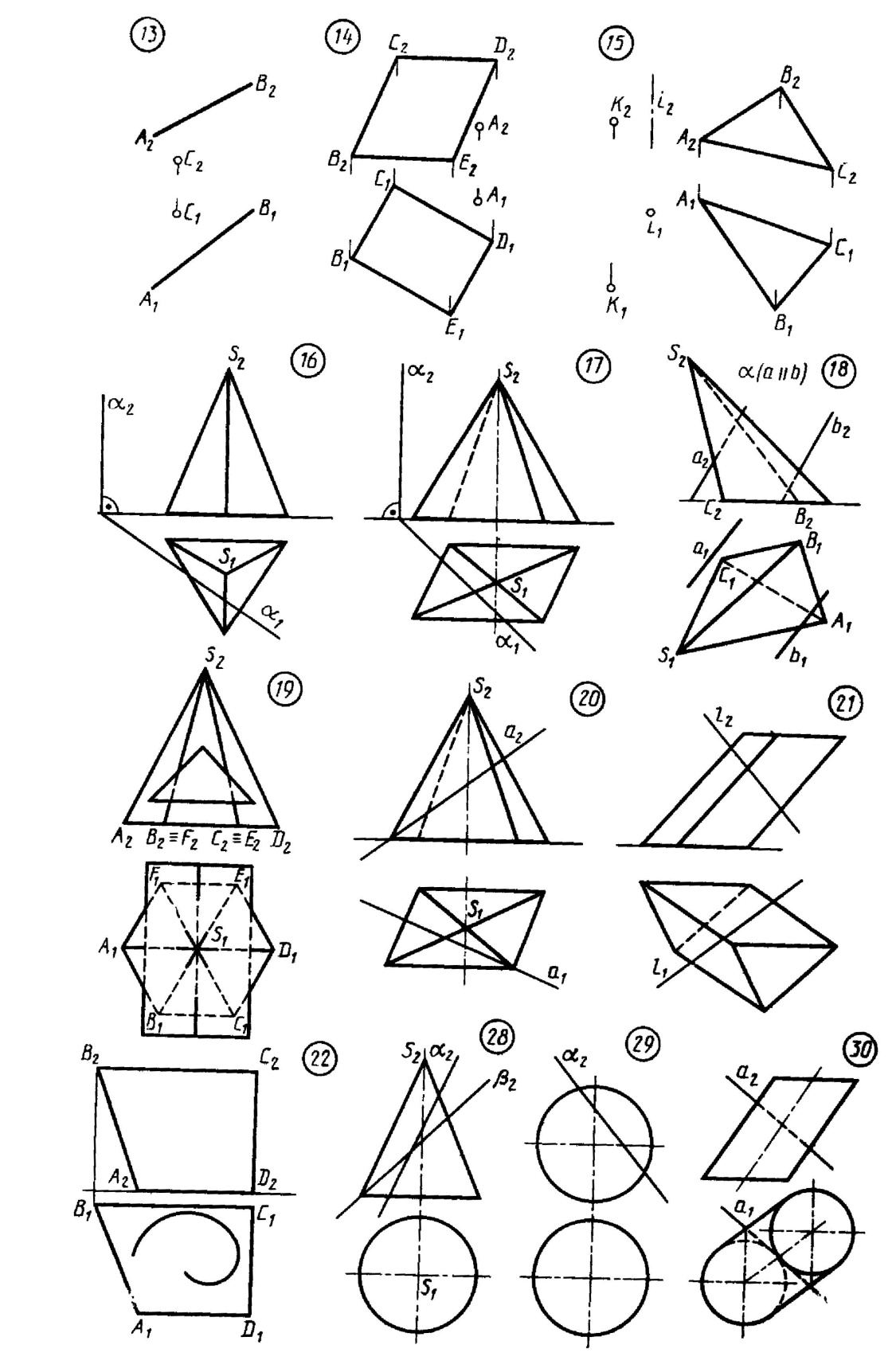
13*. Способом плоскопараллельного пе­ремещения определить расстояние от точ­ки С до прямой а(А, В)

14*. Способом гачены плоскоеu-и про­екций определить расстояние от точки А до плоскости а (б, С, D, Е).

15. Повернуть точку К вокруг оси i до совмещения с плоскостью α(А. В, С).

К теме 5. Многогранники.

16, 17, 18, 19. Построить линию пересе­чения поверхности плоскостью.

20, 21. Построить точки пересечения пря­мой с многогранников.

К теме 6. Кривые линии.

22, Достроить фронтальную проекцию плоской кривой линии, принадлежащей пло­ское г и α(А. В, С).

23. Построить винтовую линию, распо­ложенную на боковой поверхности цилинд­ра, у которого диаметр 30 мм, а высота – 60 мм,

К теме 7. Поверхности.

24. Постройте две проекции произволь­ного каноида, если его одна направляю­щая – горизонтальная линия, вторая – произвольная кривая.

25. Постройте две проекции произволь­ного прямого винтового геликоида.

26. Постройте три проекции сферы с вер­тикальным трехгранным отверстием, распо­ложенным произвольно.

27. Построить три проекции прямого кругового конуса с произвольным горизон­тальным цилиндрическим отверстием.

К теме 8. Пересечение поверхности плоскостью и прямой.

28*. Построить проекции линии пересе­чения поверхности конуса с плоскостями и и В, найти натуральную величину сече­ний Назвать, какая линия ограничивает каждое сечение.

29. Построить линию пересечения сферы и плоскости а Определить натуральную ве­личину сечения.

30*. Построить точки пересечения пря­мой а с поверхностью цилиндра.

31*. Построить точки пересечения пря­мой и с поверхностью конуса.

32*. Построить точки пересечения пря­мой а с полусферой.

К теме 9. Взаимное пересечение по­верхностей.

33. Построить линию пересечения по­верхностей пирамиды ABCS и прямого круговою цилиндра.

34. Построить линию пересечения по­верхностей конуса и призмы

35. Построить линию пересечения сферы и поверхности конуса

36. Используя способ вспомогательных секущих сфер, построить линию пересечения поверхностей двух цилиндров.

37. Используя способ вспомогательных секущих сфер, построить линию пересечения тора и поверхности цилиндра.

38. Построить линию пересечения усе­ченной половины конуса с прямым ци­линдром

39 Построить линию пересечения чет­верти сферы с цилиндром.

40. Построить линяю пересечения четвер­ти тора с вертикальной призмой.

41. Построить линию пересечения усе­ченной четверти сферы с усеченным кону­сом.

К теме 10. Развертки поверхностей.

42. Выполнить развертку перехода от квадрата к кругу.

43. Выполнить развертку перехода от круга одного диаметра к кругу другого Диаметры кругов разные и расположены в непараллельных плоскостях.

 

- 50 -

К теме 12. Аксонометрия.

44. Построить прямоугольную диметрию куба, длина ребра которого равна 30 мм. Три ребра куба лежат соответственно на осях X, Y и Z.

45. Построить прямоугольную изометрию цилиндра, диаметр основания которого ра­вен 30 мм, а высота – 40 мм. Центр ниж­него основания цилиндра расположен в точ­ке А, а ось вертикальна.

К теме 13. Проекции с числовыми от­метками. Точка. Прямая. Плоскость.

46. Определить расстояние между пря­мыми а (В, Е) и b (A, D), если известны их уклоны и отметки точек В и А.

47. Определить угол наклона и интервал прямой а(А₇, В₇), если заложение этой пря­мой равно 9 единицам.

48. Построить точку пересечения пря­мой а(А₇, В₂) с плоскостью, заданной го­ризонталью «3» и уклоном 2:1.

49. В плоскости а(А_2, В₈, С₃) провести прямую с уклоном ί = l: 5.

К теме 15. Тени в ортогональных и аксонометрических проекциях.

50. Построить тень, падающую от треу­гольника ABC на плоскости проекций, и тень, падающую от отрезка прямой а(А, Е) на плоскость треугольника.

51. Построить тень, падающую на плос­кость П₂ от окружности и описанного во­круг нее квадрата и его диагоналей.

52. Построить собственные и падающие тени призмы и падающую тень треугольни­ка ABC в ортогональных проекциях и аксо­нометрии. При построении тени от прямой а (А, В) на поверхность призмы следует воспользоваться способом «обратного луча».

53. Построить собственную тень полуци­линдра и падающие тени от карниза на по­луцилиндр и стену, а также от полуцилинд­ра на стену