
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разрешающая способность оптическихСодержание книги
Поиск на нашем сайте
Приборов
Используя даже идеальную оптическую систему (такую, для которой отсутствуют дефекты и аберрации), невозможно получить стигматическое изображение точечного источника, что объясняется волновой природой света. Изображение любой светящейся точки в монохроматическом свете представляет собой дифракционную картину, т. е. точечный источник отображается в виде центрального светлого пятна, окруженного чередующимися темными и светлыми кольцами. Согласно критерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает с первым минимумом дифракционной картины от другого (рис. 265, а). При выполнении критерия Рэлея интенсивность «провала» между максимумами составляет 80% интенсивности в максимуме, что является достаточным для разрешения линий l1 и l2. Если критерий Рэлея нарушен, то наблюдается одна линия (рис. 265, б).
1. Разрешающая способность объектива. Если на объектив падает свет от двух удаленных точечных источников S1 и S2 (например, звезд) с некоторым угловым расстоянием dy, то вследствие дифракции световых волн на краях диафрагмы, ограничивающей объектив, в его фокальной плоскости вместо двух точек наблюдаются максимумы, окруженные чередующимися темными и светлыми кольцами (рис. 266).
Рис. 266 Можно доказать, что две близлежащие звезды, наблюдаемые в объективе в монохроматическом свете, разрешимы, если угловое расстояние между ними
где l — длина волны света, D— диаметр объектива. Разрешающей способностью (разрешающей силой) объектива называется величина
где dy— наименьшее угловое расстояние между двумя точками, при котором они еще оптическим прибором разрешаются. Согласно критерию Рэлея, изображения двух одинаковых точек разрешимы, когда центральный максимум дифракционной картины для одной точки совпадает с первым минимумом дифракционной картины для другой (рис. 266). Из рисунка следует, что при выполнении критерия Рэлея угловое расстояние dyмежду точками должно быть равно j, т. е. с учетом (183.1)
Следовательно, разрешающая способность объектива
т. е. зависит от его диаметра и длины волны света. Из формулы (183.2) видно, что для увеличения разрешающей способности оптических приборов нужно либо увеличить диаметр объектива, либо уменьшить длину волны. Поэтому для наблюдения более мелких деталей предмета используют ультрафиолетовое излучение, а полученное изображение в данном случае наблюдается с помощью флуоресцирующего экрана либо фиксируется на фотопластинке. Еще большую раз решающую способность можно было бы получить с помощью рентгеновского излучения, но оно обладает большой проникающей способностью и проходит через вещество не преломляясь; следовательно, в данном случае невозможно создать преломляющие линзы. Потоки электронов (при определенных энергиях) обладают примерно такой же длиной волны, как и рентгеновское излучение. Поэтому электронный микроскоп имеет очень высокую разрешающую способность (см. § 169). Разрешающей способностью спектрального прибора называют безразмерную величину
где dl — абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются раздельно. 2. Разрешающая способность дифракционной решетки. Пусть максимум m-го порядка для длины волны l2 наблюдается под углом j, т. e.,согласно (180.3), dsinj = ml2. При переходе от максимума к соседнему минимуму разность хода меняется на l/N (см. (180.4)), где N — число щелей решетки. Следовательно, минимум l1 наблюдаемый под углом jmin, удовлетворяет условию dsinjmin = ml1 +l1/N. По критерию Рэлея, j = jmin, т.е. ml2 = ml1 +l1/N или l2/(l2 - l1) = mN. Так как l1 и l 2 близки между собой, т. е. l 2 - l1 = dl, то, согласно (183.3),
Таким образом, разрешающая способность дифракционной решетки пропорциональна порядку mспектра и числу N щелей, т. е. при заданном числе щелей увеличивается при переходе к большим значениям порядка m интерференции. Современные дифракционные решетки обладают довольно высокой разрешающей способностью (до 2×105).
Понятие о голографии
Голография (от греч. «полная запись») — особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной кар тины. Она обязана своим возникновением законам волновой оптики — законам интерференции и дифракции. Этот принципиально новый способ фиксирования и воспроизведения пространственного изображения предметов изобретен английским физиком Д. Табором (1900—1979) в 1947 г. (Нобелевская премия 1971 г.). Экспериментальное воплощение и дальнейшая разработка этого способа (Ю. Н. Денисюком в 1962 г. и американскими физиками Э. Лейтом и Ю. Упатниексом в 1963 г.) стали возможными после появления в 1960 г. источников света высокой степени когерентности — лазеров (см. § 233). Рассмотрим элементарные основы принципа голографии, т. е. регистрации и восстановления информации о предмете. Для регистрации и восстановления волны необходимо уметь регистрировать и восстанавливать амплитуду и фазу идущей от предмета волны. В самом деле, согласно формуле (144.2), учитывая, что I ~ А2, распределение интенсивности в интерференционной картине определяется как амплитудой интерферирующих волн, так и разностью их фаз. Поэтому для регистрации как фазовой, так и амплитудной информации кроме волны, идущей от предмета (так называемой предметной волны), используют еще когерентную с ней волну, идущую от источника света (так называемую опорную волну). Идея голографирования состоит в том, что фотографируется распределение интенсивности в интерференционной картине, возникающей при суперпозиции волнового поля объекта и когерентной ему опорной волны известной фазы. Последующая дифракция света на зарегистрированном распределении почернений в фотослое восстанавливает волновое поле объекта и допускает изучение этого поля при отсутствии объекта. Практически эта идея может быть осуществлена с помощью принципиальной схемы, показанной на рис. 267, а. Лазерный пучок делится на две части, причем одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны, являясь когерентными и накладываясь друг на друга, образуют на фотопластинке интерференционную картину. После проявления фотопластинки и получается голограмма — зарегистрированная на фотопластинке интерференционная картина, образованная при сложении опорной и предметной волн. Для восстановления изображения (рис. 267, 6) голограмма помещается в то же самое положение, где она находилась до регистрации. Ее освещают опорным пучком того же лазера (вторая часть лазерного пучка перекрывается диафрагмой). В результате дифракции света на интерференционной структуре голограммы восстанавливается копия предметной волны, образующая объемное (со всеми присущими предмету свойствами) мнимое изображение предмета, расположенное в том месте, где предмет находился при голографировании. Оно кажется настолько реальным, что его хочется потрогать. Кроме того, восстанавливается еще действительное изображение предмета, имеющее рельеф, обратный рельефу предмета, т. е. выпуклые места заменены вогну ыми, и наоборот (если наблюдение ведется справа от голограммы).
Рис. 267
Обычно пользуются мнимым топографическим изображением, которое по зритель ному восприятию создает полную иллюзию существования реального предмета. Рассматривая из разных положений объемное изображение предмета, даваемое голограммой, можно увидеть более удаленные предметы, закрытые более близкими из них (заглянуть за ближние предметы). Это объясняется тем, что, перемещая голову в сторону, мы воспринимаем изображение, восстановленное от периферической части голограммы, на которую при экспонировании падали также и лучи, отраженные от скрытых предметов. Голограмму можно расколоть на несколько кусков. Но даже малая часть голограммы восстанавливает полное изображение. Однако уменьшение размеров голо граммы приводит к ухудшению четкости получаемого изображения. Это объясняется тем, что голограмма для опорного пучка служит дифракционной решеткой, а при уменьшении числа штрихов дифракционной решетки (при уменьшении размеров голограммы) ее разрешающая способность уменьшается. Методы голографии (запись голограммы в трехмерных средах, цветное и панорамное голографирование и т. д.) находят все большее развитие. Применения голографии разнообразны, во наиболее важными, приобретающими все большее значение, являются запись и хранение информации. Методы голографии позволяют записывать в сотни раз больше страниц печатного текста, чем методы обычной микрофотографии. По подсчетам, на фотопластинку размером 32´32 мм можно записать 1024 голограммы (площадь каждой из них 1 мм2), т. е. на одной фотопластинке можно «разместить» книгу объемом свыше тысячи страниц. В качестве будущих разработок могут служить ЭВМ с топографической памятью, голографический электронный микроскоп, голографические кино и телевидение, топографическая интерферометрия и т. д.
Задачи
23.1. Плоская световая волна с длиной волны 0,6 мкм падает нормально на диафрагму с круглым отверстием диаметром 1 см. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля. [1) 20,8 м; 2) 13,9 м]
23.2. Дифракционная картина наблюдается на расстоянии 1 м от точечного источника монохроматического света (l = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционной картины на экране будет наиболее темным. [0,5 мм]
23.3. На щель шириной 0,2 мм падает нормально монохроматический свет с длиной волны 0,5 мкм. Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии 1 м. Определить расстояние между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума. [5 мм]
23.4. Определить число штрихов на 1 мм дифракционной решетки, если углу l /2 соответствует максимум пятого порядка для монохроматического света с длиной волны 0,5 мкм. [400 мм"1]
23.5. Узкий параллельный пучок монохроматического рентгеновского излучения падает на грань кристалла с расстоянием 0,28 нм между его атомными плоскостями. Определить длину волны рентгеновского излучения, если под углом 30° к плоскости грани наблюдается дифракционный максимум второго порядка. [140 пм]
23.6. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (l1 =578 нм и l 2 =580 нм). Длина решетки 1 см. [34,6 мкм]
Глава 24
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.011 с.) |



 (183.1)
(183.1)
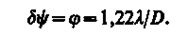
 (183.2)
(183.2)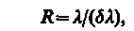 (183.3)
(183.3)




