Применение алгоритмов проектирования для решения задачи размещения элементов

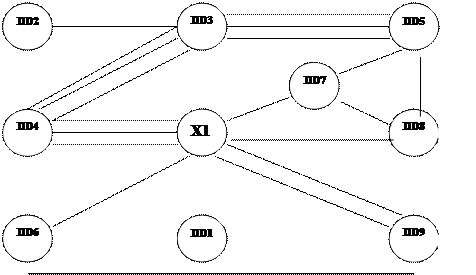
Используя заданный список цепей, построим граф схемы G (X,U). Если построение графа затруднительно, необходимо построить электрическую схему устройства, а затем приступить к построению графической модели.

Граф G (X,U) схемы представлен на рис.3.3:

 

 

 

Рисунок 3.3. – Графическая модель схемы.

Коммутационное поле состоит из десяти позиций, но мы будем работать с полем 3х3, т.к. вершина Х1 в размещении не участвует. Используем регулярное размещение элементов.

 

1	2	3
4	5	6
7	8	9

 

Рисунок 3.4. – Графическая модель коммутационного поля.

 

Далее сформируем две матрицы: матрицу смежности R и матрицу координатных длин D. Результаты представим в виде таблиц для удобства восприятия.

Матрица смежности R примет вид:

Таблица 4.

	DD1	DD2	DD3	DD4	DD5	DD6	DD7	DD8	DD9	ρi
DD1
DD2
DD3
DD4
DD5
DD6
DD7
DD8
DD9

 

В последний столбец матрицы смежности R вносим расчетное значение локальной степени вершины ρ_i, которое в дальнейшем будет применяться для определения теоретической границы суммарной длины проводников L_гр. Локальная степень вершины ρ_i определяется количеством ребер, инцидентных данной вершине.

Для построения матрицы координатных длин рассчитываются расстояния между соответствующими позициями. Расстояния измеряются в шагах координатной сетки. Расстояние между соседними позициями принимают равным одному шагу. В последнем столбце таблицы указывают суммарное количество координатных длин d_i для каждой позиции.

Матрица координатных длин D будет представлена в виде:

Таблица 5.

										di
1

 

Процесс размещения. В качестве меры приближения решения задачи к оптимальному необходимо применить сравнение общей длины проводников L(G), полученной после некоторого размещения с оценкой теоретической границы.

Для практического вычисления и оценки граничного значения длины связей L_гр все элементы треугольных матриц R и D упорядочивают в возрастающем (для R) и убывающем (для D) порядке. Затем по-членно суммируют произведение RxD этих упорядоченных последовательностей.

Формула для расчета теоретического граничного значения длины имеет вид:

L_гр = 1,2• (ΣR _ij ·D _ij) (3.1)

Расчет сводим в таблицу:

Таблица 6.

R	D	RxD	R	D	RxD

 

L_гр = 1,2•18= 21,6 ≈22

Для получения оптимального варианта размещения элементов суммарная длина связей всех проводников не должна превышать значения L_гр, т.е. L(G) < 22

Начальное размещение элементов DD1…DD9 на коммутационном поле печатной платы с установочными позициями 1…9 производим, используя алгоритм обратного размещения. Для этого:

1.Упорядочиваем элементы локальной степени вершины ρ_iматрицыRпо возрастанию.

2.Упорядочиваем элементы d_i матрицы координатных длин D по убыванию.

3.Проводим назначение элементов по позициям, назначая элемент DD9 в позицию 1, DD1 – в позицию 3 и т.д., учитывая при этом условие минимума скалярного произведения ρ·d.

Данные сводим в таблицу:

Таблица 7.

	DD9	DD1	DD6	DD7	DD8	DD2	DD4	DD5	DD3
ρ
позиция
d

 

Результаты данного алгоритма отражаем размещением элементов на коммутационном поле:

DD9 1	DD6 2	DD1 3
DD7 4	DD8 5	DD2 6
DD4 7	DD5 8	DD3 9

 

Рисунок 3.5- Начальное размещение элементов на коммутационном поле.

 

Расчет суммарной длины связи начального размещения ΣL_нр производится по формуле:

ΣL_нр=L₁+ L₂+ L₃+ L₄+ L₅+ L6+ L₇+ L₈+ L₉, где (3.2)

L₁= r₁₂·d₁₂ + r₁₃·d₁₃ + r₁₄·d₁₄ + r₁₅·d₁₅ + r₁₆·d₁₆ + r₁₇·d₁₇ + r₁₈·d₁₈ + r₁₉·d₁₉;

L₂= r₂₃·d₂₃ + r₂₄·d₂₄+ r₂₅·d₂₅ + r₂₆·d₂₆ + r₂₇·d₂₇ + r₂₈·d₂₈ + r₂₉·d₂₉;

L₃= r₃₄·d₃₄+ r₃₅·d₃₅ + r₃₆·d₃₆ + r₃₇·d₃₇ + r₃₈·d₃₈ + r₃₉·d₃₉;

L₄= r₄₅·d₄₅ + r₄₆·d₄₆ + r₄₇·d₄₇ + r₄₈·d₄₈ + r₄₉·d₄₉;

L₅= r₅₆·d₅₆ + r₅₇·d₅₇ + r₅₈·d₅₈ + r₅₉·d₅₉;

L₆= r₆₇·d₆₇ + r₆₈·d₆₈ + r₆₉·d₆₉;

L₇= r₇₈·d₇₈ + r₇₉·d₇₉;

L₈= r₈₉·d₈₉;

L₉=0.

Здесь r_mn – количество ребер, соединяющих соответствующие вершины;

d_mn – расстояние между соответствующими вершинами в шагах на конкретном варианте размещения.

Произведем расчет суммарной длины проводников для варианта начального размещения:

L₁= 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1·2=2;

L₂= 1·1 + 1·3+ 0 + 0 + 0 + 0 + 0=4;

L₃= 3·2+ 3·1 + 0 + 0 + 0 + 0 = 9;

L₄= 0 + 3·3 + 0 + 0 + 0 = 9;

L₅= 0 + 1·2 + 2·1 + 0 = 4;

L₆= 0 + 0 + 1·1 = 1;

L₇= 1·1 + 0 = 1;

L₈= 1·2 = 2;

L₉=0.

Результаты суммируются по формуле (1), в итоге получим ΣL_нр=32.

Сравнение полученного значения со значением теоретической границы суммарной длины (L_гр = 22) показывает, что начальное размещение элементов не оптимально и требуется улучшить полученный результат, т.е. достичь такого варианта размещения, когда

ΣL_нр < L_гр

Далее, применяя алгоритм парных перестановок, который заключается в по-парной перестановке элементов на коммутационном поле, отыскиваем такой вариант размещения, для которого Σ L(G)< 22.