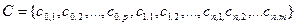Математические модели объектов проектирования радиоэлектронных средств

При решении задач в АСКП (Автоматизированных системах конструкторского проектирования) возникает необходимость выбора совокупности математических моделей, обеспечивающих необходимой информацией каждый алгоритм решения конкретной задачи.

Для каждой задачи АСКП (компоновка, размещение, трассировка) на этапе предшествующем постановке задачи, выбирается (разрабатывается) математическая модель. Это позволяет перейти от содержательной постановки задачи к формальной постановке в терминах выбранной модели.

Поскольку цели отдельных задач АСКП отличаются, то возможно для решения каждой задачи применять свою модель.

Проблема выбора (построения) моделей является важной и актуальной, так как от модели во многом зависит качество решения задач в АСКП и эффективность алгоритмических методов.

Требования, предъявляемые к математической модели:

- простота перехода от объекта к модели и обратно;

- удобство представления и обработки модели в ЭВМ;

- небольшой объем памяти компьютера, отводимый для хранения информации для модели;

- разработанность математического аппарата для работы с данной моделью (дает возможность разрабатывать высокоэффективные алгоритмы проектирования);

- информационная простота модели (возможность перехода от описания данной модели к более простой).

Математические модели, используемые при решении задач в АСКП можно разделить на две группы:

- математические модели схем;

- математические модели монтажного пространства.

Рассмотрим математические модели, построенные в рамках аппарата теории графов. Введем понятия: коммутационная схема; электрическая цепь; контакты.

Коммутационная схема устройства. Любая схема (функциональная, логическая, принципиальная, структурная) состоит из набора элементов и соединений, о которых можно сказать, что они находятся в заданном отношении. Поэтому такие схемы можно рассматривать как некоторое множество элементов X=(Х₁,Х₂,…,X_n), |X|=п и некоторое множество соединителей (называемых цепями) E=(e₁,e₂,...,e_m), |E|=m, находящихся в заданном бинарном отношении.

В схеме имеются внешние и внутренние выводы С.

 

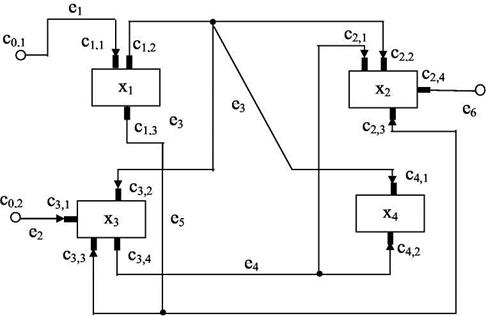
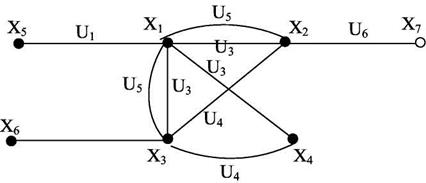
Внутренние выводы соединяют элементы схемы между собой.

Внешние выводы соединяют элементы данной схемы с элементами другой схемы.

Множество С называется множеством контактов.

Два контакта С_i,j и С_k,_е считаются связанными (соединенными), если они объединяются одной электрической цепью.

Электрическая цепь - это некоторое подмножество контактов С’ множества контактов С, принадлежащих к одному эквипотенциалу.

Контакты подмножества С’ имеют равный потенциал в принципиальной электрической схеме.

Такое представление схемы называют схемой соединений или коммутационной схемой (КС).

При построении математической модели в коммутационной схеме каждой однопотенциальной цепи ставят в соответствие число из натурального ряда.

Для решения задач компоновки, размещения и трассировки коммутационную схему можно представлять структурными математическими моделями различного вида.

Модели схем в зависимости от математического аппарата, в рамках которого разработана модель, условно разделяют на три вида:

- модели, использующие аппарат теории графов;

- модели, использующие аппарат теории гиперграфов;

- модели, использующие аппарат теории множеств.

В настоящее время наиболее широко используются модели, построенные в рамках теории графов и в первую очередь при математической постановке оптимизационных задач конструирования. Это позволяет при разработке алгоритмов решения задач конструирования использовать известные математические методы.

Рассмотрим структурные математические модели, использующие аппарат теории графов на примере условного фрагмента схемы электрической принципиальной, представленной на рис.2.1:

Рисунок 2.1 - Фрагмент схемы электрической принципиальной.

 

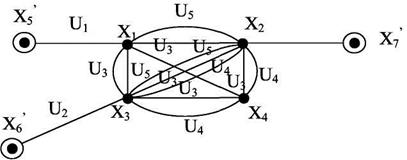
Одним из способов представления схемы устройства структурной математической моделью является ее интерпретация неориентированным связным графом G=(X,U), где Х={х_i} i = 1,…, n множество вершин G, U - множество ребер U={u_i,j}, определяющих отношения между элементами множества X.

Для построения графа G, необходимо задать между элементами множества Х={х_i} и элементами схемы (к элементам схемы относятся сами приборы и внешние контакты схемы), взаимнооднозначное соответствие, в том числе между элементами множества ребер U={u_i,j}, и элементами множества электрических цепей Е ={e_i}.

Для схемы, приведенной на рис.2.2 математическая модель M1 представляет неориентированный граф G₁=(X,U) с мультичислом, равным 3:

Рисунок 2.2 - Математическая модель M1.

Модель M1 удобна для решения задач компоновки и размещения.

Для решения задач определения планарности и трассировки математическая модель M1 неудобна из-за больших искажений между моделью и коммутационной схемой.

Рисунок 2.3 - Математическая модель М2.

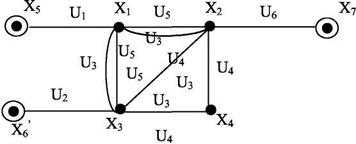
Модификацией математической модели M1 является математическая модель М2, в которой полные подграфы, моделирующие цепи e из E, заменяются покрывающими их деревьями (рис. 2.3).

 

 

Разновидностью математической модели М2 является представление коммутационной схемы графом G=(X, U), в котором все покрывающие деревья являются звездными подграфами с центральной вершиной X_i, соответствующей началу цепи e_i (рис. 2.4).

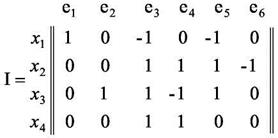
Рисунок 2.4 - Математическая модель М3.

Общий недостаток приведенных математических моделей - фиксированные деревья могут ухудшить качество компоновки. Тем не менее, приведенные модели M1, M2, МЗ наиболее просты при решении практических задач.

Коммутационная схема также может быть представлена в виде двудольного ориентированного графа D=(X_Ụ C_ỤE, U). В этом случае граф задают матрицей инцидентности I= || i_k,p ||, элементы i_k,p, которой равны либо -1, либо 0, либо 1.

i_k,p = -1, если цепь е_р - выходная для элемента х_к; i_k,p = 0, если цепь е_р не связана с элементом х_к; i_k,p = 1, если цепь е_р- входная для элемента х_к.

Для фрагмента коммутационной схемы, представленной на рисунке 2.1, матрица I запишется следующим образом:

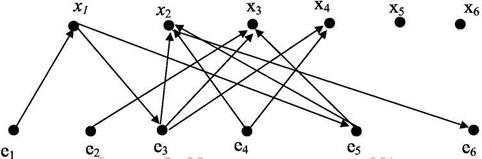
Номера столбцов данной матрицы соответствуют электрическим цепям {е_1, е₂,...е₆), а номера строк соответствуют элементам схемы {x_1, х₂, х₃, х₄). Соответствующая этой интерпретации коммутационной схемы математическая модель М4 представлена на рис.2.5:

 

 

Рисунок 2.5 - Математическая модель М4

Математическая модель М4 применяется для разработки алгоритмов трассировки соединений и, когда требуется различать входы и выходы логических элементов.

Когда матрицы, представляющие граф, сильно разрежены, т.е. имеют мало ненулевых элементов, хранение информации в матричной форме не эффективно. В этом случае удобной формой представления матриц являются списки соединений.