
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение параметров пласта по данным исследования вертикальных скважин на нестационарном режиме фильтрации газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нестационарные методы исследования газовых скважин базируются на процессах перераспределения давления в пласте при их пуске в работу и после остановки. Характер и темп распределения давления в пласте зависят от свойств газа и пористой среды. Связь темпа и характера распределения давления в пласте при пуске и остановке скважин указывает на возможность использования изменения давления во времени для определения фильтрационных и емкостных свойств пласта. Между фильтрационными и емкостными параметрами пласта и характером распределения давления имеется функциональная зависимость, которая используется для определения параметров пористой среды. Для получения аналитической зависимости между распределением давления и параметрами пласта считается, что скважина расположена в центре круговой залежи конечного или “бесконечного” размера с постоянными толщиной, пористостью, проницаемостью и, что если пласт конечных размеров, то до достижения контура питания условия на контуре пласта не влияют на работу скважины, и т.д. Если распределение давления достигло контура, то начинается общее истощение залежи. Существуют два нестационарных процесса, позволяющие определить параметры газоносного пласта путем: 1. Снятия изменения давления во времени после остановки скважины, т.е. процесс восстановления давления (КВД); 2. Снятия изменения давления и дебита после пуска скважины в эксплуатацию, т.е. снятие процесса стабилизации давления и дебита (КСДиД). Для мгновенной остановки вертикальной скважины, работавшей до закрытия с дебитом Q0 и забойным давлением Рз.0, при t=0, формулу нелинейного нестационарного притока газа можно записать в виде:
где где Рз.0, Рз(t) – забойное давление перед закрытием скважины и в момент времени t после ее закрытия; æ – пьезопроводность; t – время отсчитываемое с момента мгновенного закрытия скважины; Rс.пр – приведенный радиус; b – коэффициент фильтрационного сопротивления при квадратичном слагаемом в уравнении притока газа; μ, Z – коэффициенты вязкости и сверхсжимаемости газа; h – толщина пласта; k – проницаемость. Расчетная формула при линейном законе фильтрации для процесса восстановления давления в вертикальной газовой скважине при мгновенном ее закрытии в “бесконечном” пласте в виде:
а в пласте конечных размеров в виде:
Формулы (5.3) и (5.4) для определения параметров пласта пригодны только вблизи реальной скважины фильтрация подчиняется двучленному закону сопротивления. Влияние несовершенства также сказывается, только внутри этой области. За пределами этой зоны скорость достаточно низкая, что вызвано увеличением площади фильтрации и, поэтому закон фильтрации - линейный. Принятые условия применимости формул (5.1) и (5.3) для несовершенных газовых скважин с нарушением линейного закона вблизи скважины, вскрывшей “бесконечный” пласт, допускают, что на стенке фиктивной укрупненной скважины радиусом R0 восстановление давления описывается формулой, аналогичной формуле (5.3), но с заменой Rc на R0:
Связь между давлением на стенке фиктивной скважины радиусом R0 и реальной радиусом Rc для момента времени t описывается формулой:
где Q(t) – приток газа в укрупненную скважину. При t=0 в формуле (5.6) вместо Q(t) будет постоянный дебит перед закрытием Q0,где
l – коэффициент макрошероховатости; С1, С2 – коэффициенты несовершенства. Одним из существенных факторов, влияющих на процесс восстановления давления, является приток газа к скважине после ее закрытия Q(t). Установлено, что влияние притока на радиус укрупненной вертикальной скважины, за пределами которой имеет место линейный закон фильтрации, сказывается до достижения неравенства: Если обозначить:
то процесс восстановления Рз(t) с учетом притока газа после закрытия можно представить в виде:
Построенная в координатах Процесс восстановления давления на стенке укрупненной скважины, вскрывшей пласт конечных размеров, описывается формулой (5.4). Связь между давлением на стенках укрупненной и реальной скважин определяется формулой (5.6). Для пласта конечных размеров процесс восстановления давления в скважине с учетом притока газа может быть описан при известной величине Q(t),значение которой определяется формулой:
где
Из уравнений (5.4), (5.6) и (5.11) получена зависимость:
При больших значениях t величина
Если обозначить через:
то формула для обработки кривой восстановления давления в скважине, вскрывшей пласт конечных размеров, будет иметь вид:
Обработанная в координатах Параметры пластов, определяемые по кривым восстановления, а также по кривым стабилизации давления и дебита, относятся к зоне за пределами укрупненной скважины. Прибавление к этой зоне призабойной зоны реальной скважины в конечном итоге практически не влияет на процесс восстановления давления в укрупненной скважине. Влияние призабойной зоны отражается в основном на начальном участке кривых восстановления и стабилизации давления. Методы обработки КВД Расчетные формулы для определения по КВД параметров пласта получены для пласта конечного и “бесконечного” размеров, в которых находится исследуемая скважина. Формулы, полученные для “бесконечного” пласта, применяются в тех случаях, когда в процессе исследования скважины, границы области дренирования не сказываются на поведении этой скважины. Обработка КВД, снятой в скважине для условия “бесконечного” пласта, зависит от продолжительности ее работы до остановки. Если время работы скважины Т до снятия КВД значительно больше времени, необходимого для восстановления давления, t (Т≥20∙t), то КВД обрабатываются по формуле:
Обозначения, принятые в формулах (5.17) и (5.18) аналогичны обозначениям в формуле (5.1). Для определения параметров пласта необходимы результаты измерения обработать в координатах P2з(t) от lg t. Такая обработка данных исследования по формуле (5.10) позволяет определить α как отрезок, отсекаемый на оси P2з(t), и β как тангенс угла наклона прямой. При размерностях Q0 – тыс.м3/с, μ в Па∙с, æ – м2, h – м, Рат – Па, Т – К величина β будет определяться формулой: β=4,23Q0μплZплТпл/khТст (5.19) По найденным значениям α и β определяют проводимость пласта kh/μ, а при известном коэффициенте b величину
Если скважина совершенна, то Rc.пр=Rc,и тогда
Так как æ=kPnл/mμ, то при известных α, β и b определяют:
При известных коэффициентах æ, α, β и b можно вычислить приведенный радиус скважины:
В случае, когда продолжительность работы скважины перед закрытием Т соизмерима с продолжительностью процесса восстановления давления t, т.е. Т<20∙t, то обработку следует вести по формуле:
Формула (5.16), полученная для ограниченного пласта, нужно использовать в тех случаях, когда в процессе исследования скважины на ее поведении сказывается условие на границе пласта, например при влиянии работы соседних скважин, расположенных в кусте. В таких случаях результаты измерения обрабатываются в координатах α1=lg(1,11·β) и β1=2,51æ/R2к (5.24)
где Rк – радиус контура питания, на котором давление в процессе снятия КВД остается постоянным. Определив из графика коэффициент α1 с помощью формулы (5.24) вычисляют β и далее kh/μ, а также, используя значения β и β1 другие параметры пласта. В частности, параметр æ/R2к=β1/2,51 и газонасыщенный объем залежи, дренируемой исследуемой скважиной: V=πmhR2к=77,79khPпл/μβ1 (5.25)
При известном Rк величину mh определяют по формуле:
|
|||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 1053; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.159.5 (0.011 с.) |

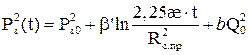 (5.1)
(5.1)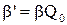 и
и 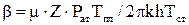 (5.2)
(5.2)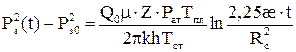 , (5.3)
, (5.3)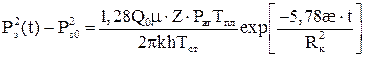 (5.4)
(5.4)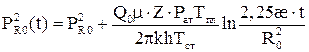 (5.5)
(5.5)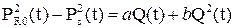 , (5.6)
, (5.6)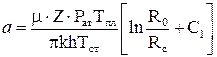 ,
, 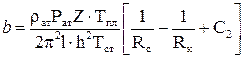 (5.7)
(5.7)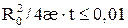 или
или 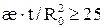
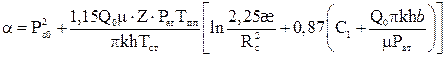 (5.8)
(5.8)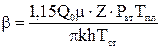 (5.9)
(5.9)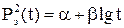 (5.10)
(5.10)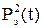 от lg t КВД позволяет определить коэффициенты α и β, а по ним коэффициенты проницаемости, проводимости, пьезопроводности и др.
от lg t КВД позволяет определить коэффициенты α и β, а по ним коэффициенты проницаемости, проводимости, пьезопроводности и др.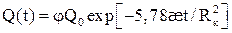 (5.11)
(5.11)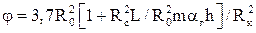 (5.12)
(5.12) (5.13)
(5.13)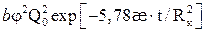 стремится к нулю и формула (5.13) приобретает вид:
стремится к нулю и формула (5.13) приобретает вид: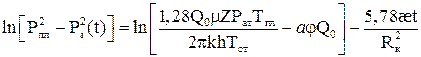 (5.14)
(5.14)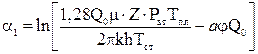 ;
; 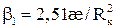 (5.15)
(5.15)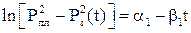 (5.16)
(5.16)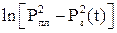 от t кривая восстановления давления позволяет определить коэффициенты уравнения α1 и β1; а по ним и параметры пласта. Формулу (5.16) можно использовать при
от t кривая восстановления давления позволяет определить коэффициенты уравнения α1 и β1; а по ним и параметры пласта. Формулу (5.16) можно использовать при 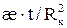 ≥0,06. Если фильтрация газа в скважине не подчиняется линейному закону, то начальный участок кривой начинает отклоняться от стандартной формы до тех пор, пока
≥0,06. Если фильтрация газа в скважине не подчиняется линейному закону, то начальный участок кривой начинает отклоняться от стандартной формы до тех пор, пока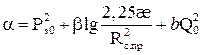 (5.17)
(5.17)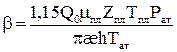 ;
; 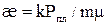 (5.18)
(5.18)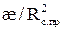 по формуле:
по формуле: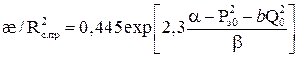 (5.20)
(5.20)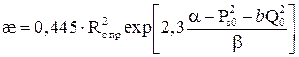 (5.21)
(5.21)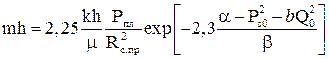 или mh=hkPnл/æμ (5.22)
или mh=hkPnл/æμ (5.22)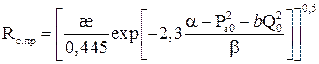
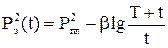 (5.23)
(5.23)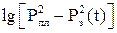 от t, в результате определяются α1 как отрезок, отсекаемый на оси
от t, в результате определяются α1 как отрезок, отсекаемый на оси 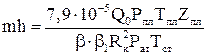 (5.26)
(5.26)


