
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вертикальный градиент давленияСодержание книги
Поиск на нашем сайте
Вертикальный градиент давления – это изменение давления при перемещении на единицу высоты. Основное уравнение статики:
∆Р = - ρg∆z,
где ρ – средняя плотность воздуха в слое ∆z, кг/м3; ∆Р – изменение давления при изменении высоты, гПа. Разделим обе части уравнения статики на ∆z. Gв = - ∆Р/∆z = ρg или Gв = g/RT. Вертикальный градиент давления выражается в гПа/100 г. Барическая ступень – высота, на которую нужно подняться или опуститься, чтобы давление изменилось на 1 гПа. Барическая ступень (м/гПа) – величина, обратная вертикальному градиенту давления.
h = RT/g = [2,87 · 106 (273,15 + t)]/(980,6*P) ≈ 8000 (1+αt)/P, (м/гпа),
α – коэффициент температурного расширения, равный 0,004. (1/273=0,004). Если пренебречь незначительными изменениями ускорения силы тяжести, то барическая ступень зависит только от плотности воздуха. Так как плотность воздуха с высотой уменьшается, то барическая ступень при увеличении высоты растет. При одном и того же давлении Р барическая ступень большее в теплом воздухе, чем в холодном. При температуре 0 0С и давлении 1000 гПа барическая ступень равняется 8 м/гПа. При повышении температуры барическая ступень увеличивается в (1+αt) раз, то есть на 0,4 % на каждый градус нагревания. В метеорологии принято понятие Международной стандартной атмосферы. В Международной стандартной атмосфере значения давления, температуры и других параметров рассчитаны к высотам 200 км. За начальный уровень принят уровень моря, на котором давление считается равным 1013,3 гПа, а температура воздуха 15 °С. К высоте 11 км стандартная атмосфера политропная (температура с высотой изменяется линейно) и имеет вертикальный градиент температуры 0,65 °С/100 г, от 11 до 30 км она является изотермической и имеет температуру (-56,5 °С).
Однородная атмосфера Однородная атмосфера – это слой воздуха, где плотность воздуха не изменяется с высотой. В однородной атмосфере изменение давления с высотой определяется соотношением: Р2= Р1 - rg (z2 – z1), (3.8)
где Р1 и Р2 – давление на высотах z1 и z2 соответственно; r - плотность воздух, кг/м3; g – ускорение свободного падения, м/с2.
Изотермическая атмосфера Изотермическая атмосфера – это слой воздуха, где температура воздуха не изменяется с высотой. В изотермической атмосфере изменение давления с высотой определяется соотношением:
Политропная атмосфера Политропная атмосфера – это слой воздуха, где температура воздуха с высотой изменяется линейно, то есть вертикальный градиент температуры имеет постоянную величину. В политропной атмосфере изменение давления с высотой определяется соотношением
где g - вертикальный градиент температуры, 0С/100 г; Т1 – температура (R) на высоте z1 (м). Реальная атмосфера Формула Лапласа есть одним из интегралов основного уравнения статики. Она имеет вид:
z2 – z1 = 18400 (1 + at) (1 +0,378 e/p) (1 + 0,0026 cosj) (1 + bz) lg Р1/Р2, (3.11)
где Р1 и Р2 – давление на уровнях z1 и z2; z = (z1 + z2) /2 - высота над уровнем моря рассмотренного пули; t, e, Р – средние по высоте значения температуры (0С), парциального давления водной пари и атмосферного давления в рассмотренном пласте; j - широта места; b - коэффициент, равный 3,14*10-7 г-1 для горных местностей; α – коэффициент, равный 0,004; множитель (1+0,378 e/p) учитывает влажность воздуха; множители (1+ 0,0026 cosj) и (1 + β·z) характеризуют зависимость ускорения свободного падения от широты и высоты места над уровнем моря. На практике часто пользуются сокращенной формулой Лапласа;
z2 - z1 = 18400 (1+αt) lg P1/P2 . (3.12)
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.34.143 (0.009 с.) |

 , (3.9)
, (3.9)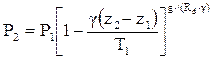 , (3.10)
, (3.10)


