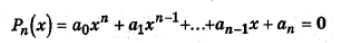Элементы теории алгоритмов. Интуитивное понятие алгоритма и его характерные черты. Необходимость уточнения понятия алгоритма.

Элементы теории алгоритмов. Интуитивное понятие алгоритма и его характерные черты. Необходимость уточнения понятия алгоритма.

Понятие алгоритма принадлежит к числу основных понятий математики. Оно прошло большой путь развития. Еще в период зарождения математики в ней стали возникать различные вычислительные процессы чисто механического характера, c помощью которых искомые величины целого класса задач вычислялись последовательно из данных исходных величин по определенным правилам. Со временем такие процессы в математике получили название алгоритмов. Примерами алгоритмов являются:

1. Правила выполнения арифметических действий над числами.

2. Правило отыскания наибольшего общего делителя (алгоритм Евклида).

3. Правило извлечения квадратного корня.

4. Правило отыскания решений квадратного уравнения.

5. Правило отыскания производной многочлена n-ой степени.

6. Правило интегрирования рациональной функции.
В каждом из приведенных примеров приходится иметь

дело с классом однотипных задач, или, как говорят, с массовой проблемой. Задачи такого класса отличаются друг от друга значениями входящих в них параметров. Так, в задаче отыскания решения квадратного уравнения ах² + bх + с = 0 участвует три параметра а, b и с; меняя их, получаем различные задачи одного класса.

В связи со сказанным можно дать следующее определение понятия алгоритма.

Алгоритмом называется общий единообразный, точно определенный способ решения любой задачи из данной массовой проблемы.

Такое определение нельзя считать строгим. Действительно, в нем встречаются слова, точный смысл которых

не установлен. В частности, это касается слова «способ». В связи с этим это не строгое определение алгоритма называют интуитивным.

Отметим характерные черты понятия алгоритма.

1. Дискретность алгоритма. Алгоритм - это процесс последовательного построения величин таким образом, что в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин получается по определенному закону из системы величин, имевшихся в предыдущий момент.

2. Детерминированность алгоритма. Система величин, получаемых в какой-то не начальный момент, однозначно определяется системой величин, полученных в предшествующие моменты времени.

3. Элементарность шагов алгоритма. Закон получения последующей системы величин из предшествующей должен быть простым.

4. Массовость алгоритма. Начальная система величин может выбираться из некоторого потенциально бесконечного множества.

5. Результативность алгоритма. Последовательный процесс построения величин должен быть конечным и давать результат, то есть решение задачи.

Алгоритмы, в которых основную роль играют математические действия, называются численными алгоритмами. От численных алгоритмов отделяют логические алгоритмы игр. В качестве примера, дающего логический алгоритм, рассмотрим следующую игру.

Имеется 15 предметов. В игре участвуют двое: начинающий и противник. Каждый игрок по очереди берет один, два или три предмета. Выигрывает тот, кто берет последний предмет. Какой стратегии в игре должен придерживаться начинающий, чтобы выиграть?

Выигрышная стратегия начинающего может быть описана в форме следующей таблицы:

 

Номер хода	Ход начинающего	Ход противника
		n
	4-n	т
	4-m	p
	4- р

Действительно, в итоге такой стратегии начинающий возьмет 3 + (4 - n) + (4 - m) + (4 - р) - 15 - {n+ m + р) предметов, а противник возьмет n + m + р предметов, т.е. в сумме они возьмут 15 предметов, и последний предмет будет взят начинающим.

Слово «алгоритм» происходит от имени узбекского математика XIII века Абу Абдалла Мухаммед ибн Муса ал Хорезми ал Меджуси. Оно претерпело эволюцию: ал Хорезми - ал Горезми - алгоритм.

Уточнение понятия алгоритма

В истории математики накопилось много случаев длительных и часто безрезультатных поисков тех или иных алгоритмов. При этом естественно возникало сомнение в существовании алгоритма.

Одним из ярких примеров такого случая является история решения десятой проблемы Д. Гильберта.

В 1900 году на втором международном математическом конгрессе в Париже немецкий математик Давид Гильберт огласил список 23 трудных проблем, на важность решения которых он обращал внимание математической общественности. Среди них была и следующая 10-ая проблема Гильберта: требуется выработать алгоритм, позволяющий для любого диофантова уравнения выяснить, имеет ли оно целочисленное решение.

Рассмотрим всевозможные диофантовы уравнения, т.е. уравнения вида Р = 0, где Р является многочленом

с целочисленными коэффициентами. Такими будут, например, уравнения

х² + у² - 2хг = 0,

10х⁵ + 7х² + 5 = 0,

из которых первое с тремя неизвестными, а второе с одним неизвестным. В общем случае рассматривают уравнения с любым числом неизвестных. Такие уравнения могут иметь целочисленные решения, а могут и не иметь.

Так, уравнение х² + у² - 2хг = 0 имеет бесконечное множество целочисленных решений, а уравнение

10х⁵ + 7х² + 5 = 0 таких решений не имеет.

Для частного случая диофантова уравнения с одним неизвестным давно известен алгоритм, позволяющий найти все его целочисленные решения. Установлено, что если уравнение

 

с целочисленными коэффициентами имеет целый корень, то он обязательно является делителем a_n. В связи с этим можно предложить такой алгоритм:

1) Найти все делители числа a_n: d₁ d₂,..., d_n.

2) Вычислить P_n(x} для каждого из делителей числа а_n

3) Если при некотором i из совокупности 1,2,...,n

P_n(d_i) = 0, то d_t - корень уравнения. Если при всех i = 1,2,...,k P_n(d_j)¹0, то уравнение не имеет целочисленных решений.

Поиски решения десятой проблемы Гильберта привлекли внимание многих математиков и длились около 70 лет. Только в 1968 году молодым математиком Ю. Матиясевичем было доказано, что нет алгоритма, дающего решение поставленной задачи.

Интуитивное определение алгоритма хотя и не строгое, но настолько ясное, что не дает оснований для сомнений в тех случаях, когда речь идет о найденном алгоритме решения конкретной задачи.

Положение существенно меняется, когда возникает алгоритмическая проблема, решение которой не найдено, и требуется установить, имеет ли она решение.

Действительно, в этом случае нужно либо доказать существование алгоритма, либо доказать его отсутствие.

В первом случае достаточно дать описание фактического процесса, решающего задачу. В этом случае достаточно и интуитивного понятия алгоритма, чтобы удостовериться в том, что описанный процесс есть алгоритм.

Во втором случае нужно доказать несуществование алгоритма, а для этого нужно точно знать, что такое алгоритм. Между тем для общего понятия алгоритма точного определения до тридцатых годов XX века не было, и поэтому выработка такого определения стала одной из важных задач современной математики. При формулировке этого определения пришлось преодолеть многие трудности.

Во-первых, такое определение должно было правильно отражать сущность интуитивного определения алгоритма.

Во-вторых, оно должно было быть совершенным с точки зрения формальной точности.

И наконец, различные исследователи этой проблемы исходили из разных технических и логических соображений, и вследствие этого было выработано несколько определений алгоритма. Однако со временем выяснилось, что все эти определения равносильны, т.е. определяют одно и то же понятие. Это и есть современное понятие алгоритма.

В подходах к определению понятия алгоритма можно выделить три основных направления.

Первое направление связано с уточнением понятия эффективно вычислимой функции. Этим занимались А. Черч, К. Гедель, С. Клини. В результате был выделен класс так называемых частично-рекурсивных функций, имеющих строгое математическое определение. Анализ идей, приведших к этому классу функций, дал им возможность высказать гипотезу о том, что класс эффективно вычислимых функций совпадает с классом частично рекурсивных функций.

Второе направление связано с машинной математикой. Здесь сущность понятия алгоритма раскрывается путем рассмотрения процессов, осуществляемых в машине. Впервые это было сделано Тьюрингом, который предложил самую общую и вместе с тем самую простую концепцию вычислительной машины. Ее описание было дано Тьюрингом в 1937 году. При этом Тьюринг исходил лишь из общей идеи работы машины как работы вычислителя, оперирующего в соответствии с некоторым строгим предписанием.

Третье направление связано с понятием нормальных алгоритмов, введенным и разработанным российским математиком А. А. Марковым.

 

Определение нормального алгоритма. Примеры. Принцип Маркова. Композиция нормальных алгоритмов.

Основная операция при работе алгоритмов Маркова – это переработка слов в некотором алфавите А. Алфавитом называется всякое непустое конечное множество символов, а сами символы – буквами. Словом в алфавите А называется всякая конечная последовательность букв данного алфавита.

Эта переработка заключается в производстве некоторого количества замен определенных последовательностей символов. Эти замены совершаются в строго определенном порядке, а именно: после каждой замены алгоритм читается с самого начала, а слово анализируется с самого первого символа. В отличие от машин Тьюринга, алгоритмы Маркова выполняются без какого – либо устройства, осуществляющего движения и имеющего внутреннюю память.

Алгоритм представляет собой совокупность строк определенного вида, причем порядок строк имеет важнейшее значение. Формат строки следующий:

{a_i} à {b_j} [•], где

{a_i} – последовательность символов, которая ищется в слове

à – знак перехода к операции записи

{b_j} – последовательность символов, которая записывается вместо найденной [•] – знак принудительного окончания алгоритма (необязательный параметр).

Окончание работы алгоритма происходит в тот момент, когда выполняется строка, содержащая знак принудительной остановки, либо тогда, когда более ни одна строка не может быть выполнена (в слове нет ни одной из искомых последовательностей символов).

Например, алгоритм, состоящий из одной строки, вида 0 à * будучи примененным к слову в алфавите {0,1}, заменит все нули на звездочки.

В свою очередь алгоритм0 à * • будучи примененным к слову в алфавите {0,1}, заменит на звездочку первый встреченный ноль.

Довольно сложная для реализации на машинах Тьюринга задача сортировки слова по возрастанию, допустим в алфавите {0,1,2}, решается при помощи Маркова весьма изящно:

20 à 02

10 à 01

21 à 12

Некоторые задачи переработки слов нельзя решить без расширения алфавита. Например, дано произвольное двоичное слово. Надо убрать из него два первых знака. Рассмотрим алгоритм вида:

00 à •

01 à •

10 à •

11 à •

Если в слове случайно первыми двумя символами были нули (например, «001011»), то алгоритм действительно выполнит указанную задачу. Также работа закончится успешно, если в слове ни разу не встретилось два нуля подряд, а первыми символами оказалась пара 01 (например, «01011101»). Но в слове 1100101 выбросятся два нуля, которые вовсе не являются первыми символами слова. В этом случае существующий алфавит надо расширить вспомогательными буквами, которых нет в начальном слове, и которые появляются в ходе вычисления. По сути, это некоторые аналоги внутренней памяти (состояний машин Тьюринга). Они вводятся с помощью формулы λ à α (α – вспомогательная буква) или, что более корректно, пары формул

λ 0 à α 0

λ 1 à α 1

Применив такие правила к слову λ 1100101 λ, получим: λ α 1100101 λ.

Дальше мы перемещаем эту букву по слову вправо, стирая и отсчитывая символы

(стерли первый):

α 0 à β

α 1 à β

(стерли второй):

β 0 à •

β 1 à •

Однако если мы расположим эти строки в обычном порядке, а именно:

λ 0 à α 0

λ 1 à α 1

α 0 à β

α 1 à β

β 0 à •

β 1 à •

алгоритм будет работать совсем не так, как хотелось бы. В частности вся его деятельность будет сводиться к созданию бесконечно большого числа символов α поочередно со стиранием символов слова. Это связано с тем, что после выполнения каждой замены управление передается снова первой строке, а слово анализируется с левого символа. Поэтому чаще всего алгоритм пишется как бы «снизу-вверх», т.е. в самом начале ставятся строки, относящиеся к группе «окончание алгоритма», далее «тело программы» и в самом низу блок «инициализация», которая будет выполняться только однажды, а затем управление перейдет к более ранним строкам.

Правильный алгоритм выглядит следующим образом.

β 0 à •

β 1 à •

α 0 à β

α 1 à β

λ 0 à α 0

λ 1 à α 1

Ту же самую задачу можно решить, используя всего один дополнительный символ:

α00 à•

α01 à•

α10 à•

α11 à•

α0 à•

α1 à•

λ 0 à α 0

λ 1 à α 1

 

Определение рекурсивных и частично рекурсивных функций. Примеры. Вычислимые функции. Частично рекурсивные и общерекурсивные функции

Для алгоритмических проблем типичным является то обстоятельство, что требуется найти алгоритм для решения задачи, в условия которой входят значения некоторой конечной системы целочисленных параметров x₁, x₂,…, x_n, а искомым результатом также является целое число y. Следовательно, стоит вопрос о существовании алгоритма для вычисления значений числовой функции y, зависящей от целочисленных значений аргументов x₁, x₂,…, x_n.

Определение 1. Функция называется эффективно вычислимой, если существует алгоритм, позволяющий вычислить ее значения.

Переход от алгоритма к эффективно вычислимой функции дает определенные преимущества. Дело в том, что все требования, которые предъявляются к алгоритмам, выполняются и для совокупности всех вычислимых функций, которая получила название совокупности рекурсивных функций.

Класс вычислимых функций можно построить следующим образом. Для начала выбираются простейшие функции:

1. l(x) = x + 1 (оператор сдвига),

2. O(x) = 0 (оператор аннулирования),

3. I_n^m(x₁, x₂,…, x_n) = x_m (оператор проектирования).

Ясно, что все три простейшие функции всюду определены и интуитивно вычислимы.

Далее вводятся операции над функциями.

1. Суперпозиция функций. Пусть определены функции f₁(x₁, x₂,…, x_n), f₂(x₁, x₂,…, x_n), …, f_m(x₁, x₂,…, x_n) и функция j(x₁, x₂,…, x_m). Говорят, что функция y(x₁, x₂,…, x_n) получена суперпозицией функций f_i(x₁, x₂,…, x_n), если справедливо равенство

y(x₁, x₂,…, x_т) = j(f₁(x₁, x₂,…, x_n), f₂(x₁, x₂,…, x_n), …, f_m(x₁, x₂,…, x_n)).

Если каким-либо образом можно вычислить функции f_i для определенных значений a_i переменных x_i, то, очевидно можно вычислить и функцию y.

2. Схема примитивной рекурсии. Пусть имеются две функции j(x₂, x₃,…, x_n) и y(x₁, x₂,…, x_n, x_n+1) (n > 1). Рассмотрим новую функцию, которая удовлетворяет следующим равенствам:

f(0, x₂, x₃,…, x_n) = j(x₂, x₃,…, x_n),

f(y + 1, x₂, x₃,…, x_n) = y(y, f(y, x₂, x₃,…, x_n), x₂, x₃,…, x_n).

Отметим, что функция j зависит от n – 1 аргументов, y – от n + 1, а f – от n.

Функции, определенные с помощью таких равенств называются функциями, полученными по схеме рекурсии.

В качестве примера рассмотрим функцию f(y, x):

f(0, x) = x,

f(y + 1, x) = f(y, x) + 1.

Здесь функция j(x) = x, а y(y, f(y, x), x) = y + 1. Рассмотрим, как можно вычислить значение функции f(y, x) при y = 5, x = 2. Так как f(0, x) = j(2) = 2, то из второго равенства последовательно имеем (начиная с y = 0):

f(1, 2) = y(0, 2, 2) = 2 + 1 = 3,

f(2, 2) = y(1, 3, 2) = 3 + 1 = 4,

f(3, 2) = y(2, 4, 2) = 4 + 1 = 5,

f(4, 2) = y(3, 5, 2) = 5 + 1 = 6,

f(5, 2) = y(4, 6, 2) = 6 + 1 = 7 – искомое значение функции.

3. Операция минимизации (m-оператор). Пусть задана некоторая функция f(x, y). Зафиксируем значение x и выясним, при каком значении y f(x, y) = 0. Так как результат зависит от x, то наименьшее значение y, при котором f(x, y) = 0, есть функция от x. Принято обозначение

j(x) = my[f(x, y) = 0].

(читается: «наименьшее y такое, что f(x, y) = 0»)

Аналогично можно определить функцию для многих переменных:

j(x₁, x₂,…, x_n) = my[f(x₁, x₂,…, x_n, y) = 0].

Переход от функции f к функции j называется применением m-оператора.

Функция j может быть вычислена следующим образом:

1. Вычислим f(x₁, x₂,…, x_n, 0). Если это значение f = 0, то полагаем j(x₁, x₂,…, x_n) = 0 и завершаем вычисление. Иначе переходим к следующему шагу.

2. Вычислим f(x₁, x₂,…, x_n, 1). Если это значение f(x₁, x₂,…, x_n, 1) = 0, то полагаем j(x₁, x₂,…, x_n) = 1 и завершаем вычисление. Иначе переходим к следующему шагу. И т.д.

Если окажется, что для всех достижимых (т.е. принадлижащих области определения) значений у функция f(x₁, x₂,…, x_n, у) ¹ 0, то функцию j(x₁, x₂,…, x_n) считают неопределенной.

Тезис А. Чёрча. Каждая интуитивно вычислимая функция является частично рекурсивной.

Этот тезис нельзя доказать, так как он связывает нестрогое понятие интуитивно вычислимой функции со строгим математическим понятием частично рекурсивной функции. Но этот тезис можно опровергнуть, если построить пример функции интуитивно вычислимой, но не являющейся частично рекурсивной.

 

Примеры алгоритмически неразрешимых массовых задач.

Q4 будем записывать в виде | q4|| • В связи с этим будем пользоваться следующей таблицей кодирования: Алфавит Буква Кодовая группа Примечания Буквы адресов л Один нуль между 1     н два нуля между 1     п три нуля между 1 Внешний алфавит а0 100001 4 нуля четное число нулей, большее двух     а1 10000001 6 нулей                                   an 10...01 2(n+2) нулей     Внутрен-ний алфавит q1 1000001 5 нулей нечетное число нулей, большее трех     q2 100000001 7 нулей         ..                   qm 10...01 2(n+1)+1 нулей     Подобную строчку из единиц и нулей, составленную для функциональной схемы или для отдельной конфигурации называют шифром функциональной схемы или широм конфигурации. Пусть теперь на ленте машины Тьюринга изображен ее же собственный шифр, записанный в алфавите машины. Возможны два случая: 1. Машина применима к своему шифру, т.е. она перерабатывает этот шифр и после конечного числа тактов останавливается. 2. Машина не применима к своему шифру, т.е. машина никогда не переходит в стоп-состояние. Таким образом, сами машины (их шифры) разбиваются на два класса: класс самоприменимых и класс несамоприменимых тьюринговых машин. Поэтому возникает следующая массовая проблема: проблема распозн ваемости самоприменимости. По любому заданному шифру установить, к какому классу относится машина, зашифрованная им: к классу самоприменимых или несамоприменимых? Теорема. Проблема распознавания самоприменимости алгоритмически не разрешима. Доказательство. Предположим противное. Пусть такая машина А существует. Тогда в А всякий самоприменимый шифр перерабатывается в какой-то символ s (имеющий смысл утвердительного ответа на поставленный вопрос о самоприменимости), а всякий несамоприменимый шифр - в другой символ tt (имеющий смысл отрицательного ответа на поставленный вопрос). В таком случае можно было построить и такую машину В, которая по-прежнему перерабатывает несамоприменимые шифры в s, в то время как к самоприменимым шифрам В уже не применима. Этого можно было добиться путем такого изменения схемы машины В, чтобы после появления символа а вместо появления стоп-состояния, машина начала бы неограниченно повторять этот же символ. Таким образом, В применима ко всякому несамоприменимому шифру (вырабатывается при этом символ t) и не применима к самоприменимым шифрам. Но это приводит к противоречию. Действительно: 1) пусть машина В самоприменима, тогда она применима к своему шифру В и перерабатывает его в символ t; но появление этого символа как раз и должно означать, что В несамоприменима; 2) пусть В несамоприменима, тогда она не применима к В, что должно означать как раз, что В самоприменима. Полученное противоречие доказывает теорему.

Элементы теории алгоритмов. Интуитивное понятие алгоритма и его характерные черты. Необходимость уточнения понятия алгоритма.

Понятие алгоритма принадлежит к числу основных понятий математики. Оно прошло большой путь развития. Еще в период зарождения математики в ней стали возникать различные вычислительные процессы чисто механического характера, c помощью которых искомые величины целого класса задач вычислялись последовательно из данных исходных величин по определенным правилам. Со временем такие процессы в математике получили название алгоритмов. Примерами алгоритмов являются:

1. Правила выполнения арифметических действий над числами.

2. Правило отыскания наибольшего общего делителя (алгоритм Евклида).

3. Правило извлечения квадратного корня.

4. Правило отыскания решений квадратного уравнения.

5. Правило отыскания производной многочлена n-ой степени.

6. Правило интегрирования рациональной функции.
В каждом из приведенных примеров приходится иметь

дело с классом однотипных задач, или, как говорят, с массовой проблемой. Задачи такого класса отличаются друг от друга значениями входящих в них параметров. Так, в задаче отыскания решения квадратного уравнения ах² + bх + с = 0 участвует три параметра а, b и с; меняя их, получаем различные задачи одного класса.

В связи со сказанным можно дать следующее определение понятия алгоритма.

Алгоритмом называется общий единообразный, точно определенный способ решения любой задачи из данной массовой проблемы.

Такое определение нельзя считать строгим. Действительно, в нем встречаются слова, точный смысл которых

не установлен. В частности, это касается слова «способ». В связи с этим это не строгое определение алгоритма называют интуитивным.

Отметим характерные черты понятия алгоритма.

1. Дискретность алгоритма. Алгоритм - это процесс последовательного построения величин таким образом, что в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин получается по определенному закону из системы величин, имевшихся в предыдущий момент.

2. Детерминированность алгоритма. Система величин, получаемых в какой-то не начальный момент, однозначно определяется системой величин, полученных в предшествующие моменты времени.

3. Элементарность шагов алгоритма. Закон получения последующей системы величин из предшествующей должен быть простым.

4. Массовость алгоритма. Начальная система величин может выбираться из некоторого потенциально бесконечного множества.

5. Результативность алгоритма. Последовательный процесс построения величин должен быть конечным и давать результат, то есть решение задачи.

Алгоритмы, в которых основную роль играют математические действия, называются численными алгоритмами. От численных алгоритмов отделяют логические алгоритмы игр. В качестве примера, дающего логический алгоритм, рассмотрим следующую игру.

Имеется 15 предметов. В игре участвуют двое: начинающий и противник. Каждый игрок по очереди берет один, два или три предмета. Выигрывает тот, кто берет последний предмет. Какой стратегии в игре должен придерживаться начинающий, чтобы выиграть?

Выигрышная стратегия начинающего может быть описана в форме следующей таблицы:

 

Номер хода	Ход начинающего	Ход противника
		n
	4-n	т
	4-m	p
	4- р

Действительно, в итоге такой стратегии начинающий возьмет 3 + (4 - n) + (4 - m) + (4 - р) - 15 - {n+ m + р) предметов, а противник возьмет n + m + р предметов, т.е. в сумме они возьмут 15 предметов, и последний предмет будет взят начинающим.

Слово «алгоритм» происходит от имени узбекского математика XIII века Абу Абдалла Мухаммед ибн Муса ал Хорезми ал Меджуси. Оно претерпело эволюцию: ал Хорезми - ал Горезми - алгоритм.

Уточнение понятия алгоритма

В истории математики накопилось много случаев длительных и часто безрезультатных поисков тех или иных алгоритмов. При этом естественно возникало сомнение в существовании алгоритма.

Одним из ярких примеров такого случая является история решения десятой проблемы Д. Гильберта.

В 1900 году на втором международном математическом конгрессе в Париже немецкий математик Давид Гильберт огласил список 23 трудных проблем, на важность решения которых он обращал внимание математической общественности. Среди них была и следующая 10-ая проблема Гильберта: требуется выработать алгоритм, позволяющий для любого диофантова уравнения выяснить, имеет ли оно целочисленное решение.

Рассмотрим всевозможные диофантовы уравнения, т.е. уравнения вида Р = 0, где Р является многочленом

с целочисленными коэффициентами. Такими будут, например, уравнения

х² + у² - 2хг = 0,

10х⁵ + 7х² + 5 = 0,

из которых первое с тремя неизвестными, а второе с одним неизвестным. В общем случае рассматривают уравнения с любым числом неизвестных. Такие уравнения могут иметь целочисленные решения, а могут и не иметь.

Так, уравнение х² + у² - 2хг = 0 имеет бесконечное множество целочисленных решений, а уравнение

10х⁵ + 7х² + 5 = 0 таких решений не имеет.

Для частного случая диофантова уравнения с одним неизвестным давно известен алгоритм, позволяющий найти все его целочисленные решения. Установлено, что если уравнение

 

с целочисленными коэффициентами имеет целый корень, то он обязательно является делителем a_n. В связи с этим можно предложить такой алгоритм:

1) Найти все делители числа a_n: d₁ d₂,..., d_n.

2) Вычислить P_n(x} для каждого из делителей числа а_n

3) Если при некотором i из совокупности 1,2,...,n

P_n(d_i) = 0, то d_t - корень уравнения. Если при всех i = 1,2,...,k P_n(d_j)¹0, то уравнение не имеет целочисленных решений.

Поиски решения десятой проблемы Гильберта привлекли внимание многих математиков и длились около 70 лет. Только в 1968 году молодым математиком Ю. Матиясевичем было доказано, что нет алгоритма, дающего решение поставленной задачи.

Интуитивное определение алгоритма хотя и не строгое, но настолько ясное, что не дает оснований для сомнений в тех случаях, когда речь идет о найденном алгоритме решения конкретной задачи.

Положение существенно меняется, когда возникает алгоритмическая проблема, решение которой не найдено, и требуется установить, имеет ли она решение.

Действительно, в этом случае нужно либо доказать существование алгоритма, либо доказать его отсутствие.

В первом случае достаточно дать описание фактического процесса, решающего задачу. В этом случае достаточно и интуитивного понятия алгоритма, чтобы удостовериться в том, что описанный процесс есть алгоритм.

Во втором случае нужно доказать несуществование алгоритма, а для этого нужно точно знать, что такое алгоритм. Между тем для общего понятия алгоритма точного определения до тридцатых годов XX века не было, и поэтому выработка такого определения стала одной из важных задач современной математики. При формулировке этого определения пришлось преодолеть многие трудности.

Во-первых, такое определение должно было правильно отражать сущность интуитивного определения алгоритма.

Во-вторых, оно должно было быть совершенным с точки зрения формальной точности.

И наконец, различные исследователи этой проблемы исходили из разных технических и логических соображений, и вследствие этого было выработано несколько определений алгоритма. Однако со временем выяснилось, что все эти определения равносильны, т.е. определяют одно и то же понятие. Это и есть современное понятие алгоритма.

В подходах к определению понятия алгоритма можно выделить три основных направления.

Первое направление связано с уточнением понятия эффективно вычислимой функции. Этим занимались А. Черч, К. Гедель, С. Клини. В результате был выделен класс так называемых частично-рекурсивных функций, имеющих строгое математическое определение. Анализ идей, приведших к этому классу функций, дал им возможность высказать гипотезу о том, что класс эффективно вычислимых функций совпадает с классом частично рекурсивных функций.

Второе направление связано с машинной математикой. Здесь сущность понятия алгоритма раскрывается путем рассмотрения процессов, осуществляемых в машине. Впервые это было сделано Тьюрингом, который предложил самую общую и вместе с тем самую простую концепцию вычислительной машины. Ее описание было дано Тьюрингом в 1937 году. При этом Тьюринг исходил лишь из общей идеи работы машины как работы вычислителя, оперирующего в соответствии с некоторым строгим предписанием.

Третье направление связано с понятием нормальных алгоритмов, введенным и разработанным российским математиком А. А. Марковым.

 

Определение нормального алгоритма. Примеры. Принцип Маркова. Композиция нормальных алгоритмов.

Основная операция при работе алгоритмов Маркова – это переработка слов в некотором алфавите А. Алфавитом называется всякое непустое конечное множество символов, а сами символы – буквами. Словом в алфавите А называется всякая конечная последовательность букв данного алфавита.

Эта переработка заключается в производстве некоторого количества замен определенных последовательностей символов. Эти замены совершаются в строго определенном порядке, а именно: после каждой замены алгоритм читается с самого начала, а слово анализируется с самого первого символа. В отличие от машин Тьюринга, алгоритмы Маркова выполняются без какого – либо устройства, осуществляющего движения и имеющего внутреннюю память.

Алгоритм представляет собой совокупность строк определенного вида, причем порядок строк имеет важнейшее значение. Формат строки следующий:

{a_i} à {b_j} [•], где

{a_i} – последовательность символов, которая ищется в слове

à – знак перехода к операции записи

{b_j} – последовательность символов, которая записывается вместо найденной [•] – знак принудительного окончания алгоритма (необязательный параметр).

Окончание работы алгоритма происходит в тот момент, когда выполняется строка, содержащая знак принудительной остановки, либо тогда, когда более ни одна строка не может быть выполнена (в слове нет ни одной из искомых последовательностей символов).

Например, алгоритм, состоящий из одной строки, вида 0 à * будучи примененным к слову в алфавите {0,1}, заменит все нули на звездочки.

В свою очередь алгоритм0 à * • будучи примененным к слову в алфавите {0,1}, заменит на звездочку первый встреченный ноль.

Довольно сложная для реализации на машинах Тьюринга задача сортировки слова по возрастанию, допустим в алфавите {0,1,2}, решается при помощи Маркова весьма изящно:

20 à 02

10 à 01

21 à 12

Некоторые задачи переработки слов нельзя решить без расширения алфавита. Например, дано произвольное двоичное слово. Надо убрать из него два первых знака. Рассмотрим алгоритм вида:

00 à •

01 à •

10 à •

11 à •

Если в слове случайно первыми двумя символами были нули (например, «001011»), то алгоритм действительно выполнит указанную задачу. Также работа закончится успешно, если в слове ни разу не встретилось два нуля подряд, а первыми символами оказалась пара 01 (например, «01011101»). Но в слове 1100101 выбросятся два нуля, которые вовсе не являются первыми символами слова. В этом случае существующий алфавит надо расширить вспомогательными буквами, которых нет в начальном слове, и которые появляются в ходе вычисления. По сути, это некоторые аналоги внутренней памяти (состояний машин Тьюринга). Они вводятся с помощью формулы λ à α (α – вспомогательная буква) или, что более корректно, пары формул

λ 0 à α 0

λ 1 à α 1

Применив такие правила к слову λ 1100101 λ, получим: λ α 1100101 λ.

Дальше мы перемещаем эту букву по слову вправо, стирая и отсчитывая символы

(стерли первый):

α 0 à β

α 1 à β

(стерли второй):

β 0 à •

β 1 à •

Однако если мы расположим эти строки в обычном порядке, а именно:

λ 0 à α 0

λ 1 à α 1

α 0 à β

α 1 à β

β 0 à •

β 1 à •

алгоритм будет работать совсем не так, как хотелось бы. В частности вся его деятельность будет сводиться к созданию бесконечно большого числа символов α поочередно со стиранием символов слова. Это связано с тем, что после выполнения каждой замены управление передается снова первой строке, а слово анализируется с левого символа. Поэтому чаще всего алгоритм пишется как бы «снизу-вверх», т.е. в самом начале ставятся строки, относящиеся к группе «окончание алгоритма», далее «тело программы» и в самом низу блок «инициализация», которая будет выполняться только однажды, а затем управление перейдет к более ранним строкам.

Правильный алгоритм выглядит следующим образом.

β 0 à •

β 1 à •

α 0 à β

α 1 à β

λ 0 à α 0

λ 1 à α 1

Ту же самую задачу можно решить, используя всего один дополнительный символ:

α00 à•

α01 à•

α10 à•

α11 à•

α0 à•

α1 à•

λ 0 à α 0

λ 1 à α 1