Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение сетей Петри к задачам моделированияСодержание книги Поиск на нашем сайте
Введение Сети Петри – это инструмент исследования систем. Теория сетей Петри делает возможным моделирование системы математическим представлением её в виде сети Петри [2]. Вообще в данном определении ключевым понятием является возможность её математического представления, то есть теория сетей Петри по сути представляет собой механизм формализации процесса моделирования. Но так как задание курсового проекта звучит как моделирование процесса усвоения знаний, то мы будем вынуждены прибегать к некоторой абстракции самого процесса усвоения. С этой целью будет рассмотрена трёхуровневая модель витального интеллекта по Нечаеву [1], работы П.И. Зинченко и В.П. Зинченко по психологии [6,7], понятия о психологии мышления [13,14] и некоторые собственные мысли автора по поводу рассмотрения процесса усвоения знаний. Но следует заметить, что человека как носителя информации и накопителя (то есть как субъекта, реализующего процесс усвоения знаний) можно представить как совокупность некоторых биохимических процессов, свойств и взаимодействий. Текущий уровень науки не позволяет разбирать такие процессы на низком биофизическом уровне и позволяет работать лишь с философскими абстракциями. Тем не менее, уже сейчас есть примеры, например [8, 9], где показана принципиальная возможность низкоуровневых исследований процессов усвоения знаний (в данных опытах применялась магнитно-резонансная томография участков мозга, в [9] – для оценки восприятий людьми первичных понятий, в [8] – для оценки последствий усвоенных знаний). Кроме того в современном научном мире есть исследования, подтверждающие влияние на память человека такого процесса, как сон. К сожалению, в России действительно научных исследований на эту тему не проводится и большинство исследований процессов памяти и сна (даже не смотря на существующий в России в Екатеринбурге Клинический Институт Мозга) носят прикладной, а не фундаментальный характер и направлены больше на лечение текущих проблем, например, бессонницы и прочего. Фундаментальные же исследования проводятся в основном за рубежом. Примером таких исследований являются работы [10, 11], в которых показано влияние сна на процесс усвоения знаний. Более того, некоторые известные музыканты, в частности пианисты, говорят о том, что учат произведения во сне. Но в данной работе данная проблема будет описана кратко на основании индийской философии Турьи [12].
Общие понятия о сетях Петри Перед тем как ввести понятие о сетях Петри следует упомянуть о том, что существуют два направления развития сетей Петри. Первое направление – прикладная теория сетей Петри – связана с применением сетей Петри для моделирования систем, их анализа и анализа результатов. Второе направление – чистая теория сетей Петри – занимается разработкой средств, методов и понятий, необходимых для применения сетей Петри [2]. Очевидно, что для задач курсового проекта следует применять прикладную теорию сетей Петри. Но следует помнить, что все они опираются на чистую теорию сетей Петри, которая развивалась множеством авторов, которые, порой, определяли и разрабатывали чистую теорию по разному. В данной работе не будет рассматриваться кратность связей (то есть кратных дуг), но будут использоваться множественные фишка. Подробнее об этих понятиях будет написано ниже. Итак, сеть Петри C является четвёркой Пример сети приведён на рис. 1.
Рис. 1. Пример структуры сети Петри Но визуально удобным является графическое представление сети Петри. Если мы обозначим кружком Граф G сети Петри – это двудольный ориентированный мультиграф, G = (V,A), где Доказательства эквивалентности представлений можно найти в [2], а ниже на рис. 2 приведён рисунок сети рис. 1 в графическом представлении.
Рис. 2. Граф сети Петри, соответствующей сети на рис. 1. Следующим основным понятием, которое мы введём, будет маркировка. Маркировка µ сети Петри – есть отображение множества позиций P в множество неотрицательных целых чисел: За таким понятием скрывается довольно простая вещь – в каждый кружочек мы можем поместить точку (или несколько), которая будет отражать, грубо говоря, некоторый потенциал данной позиции. Например, промаркируем сеть рис. 1 следующим образом: (1, 0, 0, 2, 1). Здесь число, стоящее на i -й позиции в множестве обозначает количество точек в pi. Таким образом мы получаем рис. 3.
Рис. 3. Маркировка сети Петри Следующий пункт – выполнение сети. Для этого надо разобрать исходное понятие – разрешённые переходы. Переход разрешён если каждая из его входных позиций имеет по крайней мере столько фишек, сколько дуг из этой позиции в данный переход. Запуск перехода – перенос фишек через разрешённые переходы из исходных позиций в новые (из исходных позиций фишки удаляются, в новые добавляются). Тогда выполнение сети – процесс запуска переходов. В результате выполнения сети мы получаем новую маркировку µ`. Например, на рис. 3 разрешены переходы t1, t3, t4, а переход t2 запрещён. Переход t1 разрешён потому, что на входе у него позиция p1 с одной дугой и имеет одну фишку. Переход t2 запрещён, так как входящие в него позиции p2 и p3 не имеют фишек вообще. Переход t3 разрешён, так как в него входит посредством двух дуг позиция p4, имеющая 2 фишки. Переход t4 разрешён, так как имеет на входе он имеет позицию p5 с одной фишкой и одной дугой.
Рис. 4. Граф сети после запуска в сети рис.3 перехода t4
Рис. 5. Граф сети после запуска в сети рис.4 перехода t1 Можно заметить, что после последовательного выполнения переходов t4 и t1 переход t2 становится разрешённым. Функция следующего состояния –
Рис. 6. Пример сети Петри для иллюстрации понятия множество достижимости Так как все процессы моделирования усвоения знаний носят вероятностный характер по своей природе, то целесообразно определить стохастическую сеть Петри. Стохастической сетью Петри называется пара Пусть сеть имеет вид, представленный на рис. 7:
Рис. 7. Пример сети И имеет начальную маркировку:
Рис. 8. Маркировка сети рис. 7 Переход t1 разрешён, так как
Рис. 9. Маркировка сети после выполнения перехода t1 Определим вектор r:
Рис. 10. Вектор r Найдём матрицу Грама для векторов
Рис. 11. Матрица Грама Таким образом, маркировка позиции p3 после перехода будет:
Рис. 12. Маркировка позиции p3 после выполнения перехода t1
Запоминание и сон Вообще сон является плохо изученным явлением в современной науке, несмотря на активное развитие школы снов в рамках религии и эзотерики. Но недавно было показано, что сон является одним из ключевых момент при запоминании информации. В исследовании [10] было показано, что сон помогает укреплять полученные знания. Знания не носили фундаментальных характер, скорее они были рутинными или прикладными, но по результатам тестов вся группа тех, кто спал после исследований, показали лучший результат, нежели контрольная группа. Лично я считаю, что в процессе сна возможен прямой обмен между подсознательным и сверхсознательным уровнями, минуя уровень сознания. Причём такой обмен может происходить как на уровне управления через ЦММ, так и между контроллерами буферной памяти. Причём в силу отсутствия контроллеров памяти уровней СС/ПС данные преобразования могут происходить с ошибками, но характер ошибок стохастический, а, вдобавок, они могут быть полезны. Так как мозг на уровне, например, сверхсознания, будет пытаться решить задачу бессознательного уровня человеческого рефлекса, а затем это принесёт ценный опыт и в случае попадания человека в экстремальную ситуацию при работающем сознании это сознание будет решать творческую задачу и обращаться в сверхсознание, в котором данная задача уже была решена. Сон в философии Турья За основу этой части курсового проекта была взята концепция Турьи [12]. Идея концепции в том, что существует состояние сознания как целого, которое реализуется в четырёх состояниях целого сознания (в широком смысле), но отрицает разделение на объект-субъектную модель и на уровни сознания. Итак, в данной философии есть 4 состояния сознания: 1) джаграт (бодрствование); 2) свапна (сон); 3) сушупти (глубокий сон без сновидений); 4) турья (трансцендентальное чистое бытие вне трех предыдущих). Затем из данных состояний создаются комбинации, например джаграт-свапна или джаграт-джаграт. Мышление в данной философии продвигается от низшего – образного к высшему – словесному и наивысшему – мышления по достижению состояния турья. В современной индийской философии считается, что настоящий человек не способен к достижению турьи, соответственно соответствующий тип мышления для нас потерян. Но остальные состояния позволяют нам искать новые способы и методы получения знаний при существующих типах мышления. Медитационная практика и практика так называемых осознанных сновидений даёт возможность применять различные типы мышления для решения задач на глубинных метафизических и метапсихологических уровнях. Вначале я уже приводил пример о том, что практика сновидений помогает пианисту запоминать свои партии. Но можно сказать и о том, что многие области творчества могут реализовать свои потребности через сон. Единственная проблема сновидений состоит в том, что их очень мало кто помнит. Скорее всего это происходит потому, что управляющие процессы мозговых механизмов на уровне сознания вызывают сброс состояния памяти. То есть, грубо говоря, работает следующая ветка сознательного уровня:
Выходной информацией является ключ к стиранию памяти, в том числе кратковременной. А весь опыт, полученный во сне, реализуется только на уровне сверхсознания. Поэтому очень важно сохранить память о сновидении. Сделать это можно только с опытом, который должен начинаться с малого. Все высшие состояния человеку недоступны. Реально большинство людей пребывают либо в состояниях джаграт-джаграт, либо свапна. Вопреки распространённому мнению и отсутствию у большинства людей воспоминаний о сне, настоящее состояние сушупти (глубокий сон без сновидений) достигается только после длительных медитативных практик. Три состояния сознания в той или иной степени зависимы от материального влияния и сохраняют единство — в бодрствующем состоянии непосредственно (раджо-гуна), в состоянии сна со сновидениями сознание продолжает оперировать идеями, полученных от материального опыта (саттва-гуна), а после пробуждения от глубокого сна остаётся память об этом состоянии (тамо-гуна). Состояние глубокого сна, когда влияние внешнего минимально, а сознание остаётся, в какой-то мере является ключом к пониманию турьи, которое представляет собой сознание, свободное от материального влияния, но в то же время неотделимое от трёх других. В виде сети Петри это представимо следующим образом:
Рис. 38. Работа состояний сознания В схеме на рис. 38 для состояний джаграт и свапна использована модель захвата. И только после того, как отработают оба состояния, а также при наличии достаточной мотивации у индивида, он сможет перейти в состояние сушупти. Руководство пользователя С помощью инструментов, которые выбираются в панели, показанной на рис. 40 на главном полотне создаются соответствующие объекты.
Рис. 40. Панель инструментов Объекты-позиции и объекты-переходы создаются простым кликом. Объект стрелка работает следующим образом: после выбора объекта-стрелки у позиций и переходов появляются маленькие квадратики по бокам:
Рис. 41. Выбор объектов для связи После клика по одной из связи за курсором тянется красная линия, которая может завершиться на другом объекте:
Рис. 42. Линия связи После чего связь будет создана:
Рис. 43. Связь создана При выбранном объекта управления курсор можно кликнуть правой кнопкой на позицию:
Рис. 44. Свойства позиции И в получившемся окне ввести количество фишек.
Рис. 45. Ввод количества фишек
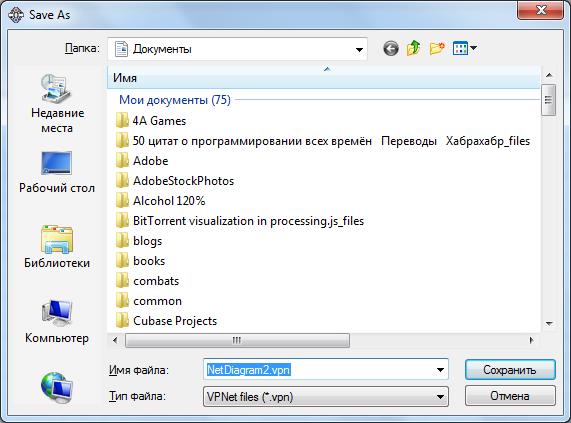
Рис. 46. Результат ввода количества фишек Также редактор поддерживает сохранение в собственном формате.
Рис. 47. Диалог сохранения файла Альтернативные проекты Вообще следует упомянуть, что в настоящее время существует достаточно мало визуальных редакторов сетей Петри. Но один проект – PIPE3 – Platform Independent Petri Net Editor – заслуживает упоминания. Данный редактор обладает более широкими возможностями, нежели разработанный в рамках курсового проекта. В частности он позволяет задавать имя каждому объекту (позиции или переходу), содержит готовые типы переходов как мгновенного и длительного, а, кроме того, сохраняет все получившиеся модели в формате XML, что позволяет работать с ними в других программах. И более того, как следует из названия, проект платформо-независимый, то есть сможет работать на любых компьютерах под управлением любых операционных систем. Вид окна данного редактора представлен ниже:
Рис. 48. Общий вид редактора PIPE3
Выводы В ходе данной работы была проведена работа по исследованию литературы по прикладному применению сетей Петри, анализ существующей литературы по психологии сознания и построение некоторых моделей Нечаева [1], применимых к процессу познания как творческому, в форме графического представления сети Петри. Следует сказать, что сеть Петри является очень хорошим механизмом, и, несмотря на некоторую возможную сложность, которая может возникнуть при первом рассмотрении, она позволяет проводить анализ процессов на более глубоком уровне за счёт разделения на позиции и переходы. Кроме того в рамках курсового проекта была разработана визуальная среда, позволяющая легко и быстро создавать модели в виде графического представления сети Петри, а также был показан альтернативный современный редактор сетей. На основании этого можно заключить, что сети Петри из чисто академического интереса в виду простоты построение в вышеупомянутых редакторах, могут найти широкое применение и в реальных учебных процессах, в частности, в нашем ВУЗе. А данная работа должна помочь молодым специалистам освоиться и изучить применимость данной технологии моделирования к реальным задачам.
Литература 1. В.В. Нечаев. Основы теории творческой деятельности. Конспект лекций по курсу. - М.: МИРЭА (ТУ), 2011. 2. Джеймс Питерсон «Теория сетей Петри и моделирование систем»: Пер. с англ.-М.:Мир, 1984.-264с. 3. Котов В.Е. «Сети Петри» М.:Наука, 1984.-160с. 4. А.А. Лескин, П.А. Мальцев, А.М. Спиридонов «Сети Петри в моделировании и управлении» Л.: Наука, 1989.-133с. 5. И.Е. Федотов «Некоторые приёмы параллельного программирования» Учебное пособие. - М.: Изд-во МГИРЭА(ТУ), 2008. - 188 с. 6. В.П. Зинченко, В.М. Мунипов, «Эргономика. Человекоориентированное проектирование техники, программного обеспечения и среды». Учебник для вузов. М., 1998 7. П.И. Зинченко «Непроизвольное запоминание» - М.: Изд-во АПН РСФСР, 1961. — 562 c 8. М. Либерман «Neuroscientists can predict your behavior better than you can» - UCLA, U of M, 2010 9. Tom M. Mitchell, Svetlana V. Shinkareva, Andrew Carlson, Kai-Min Chang, Vicente L. Malave, Robert A. Mason, Marcel Adam Just «Predicting Human Brain Activity Associated with the Meanings of Nouns» - Carnegie Mellon University, 2008 10. Erin J. Wamsley, Matthew Tucker, Jessica D. Payne, Joseph A. Benavides, Robert Stickgold «Dreaming of a Learning Task Is Associated with Enhanced Sleep-Dependent Memory Consolidation» - Current biology, 2010 11. Matthew P. Walker – «Sleep and neuroimaging» - Beth Israel Deaconess Medical Center, 2010 12. Swami B. V. Tripurari. «Brahman, Paramatma, and Bhagavan» 13. Я.А. Пономарёв «Психология творчества» М.:Наука, 1976. 14. О.К. Тихомиров «Психология мышления»: Учебное пособие. М.: Изд-во Моск. ун-та, 1984. — 272 с. 15. В. П. Кохановский и др. «Основы философии науки». М.: Феникс, 2007 г. - 608 с. Введение Сети Петри – это инструмент исследования систем. Теория сетей Петри делает возможным моделирование системы математическим представлением её в виде сети Петри [2]. Вообще в данном определении ключевым понятием является возможность её математического представления, то есть теория сетей Петри по сути представляет собой механизм формализации процесса моделирования. Но так как задание курсового проекта звучит как моделирование процесса усвоения знаний, то мы будем вынуждены прибегать к некоторой абстракции самого процесса усвоения. С этой целью будет рассмотрена трёхуровневая модель витального интеллекта по Нечаеву [1], работы П.И. Зинченко и В.П. Зинченко по психологии [6,7], понятия о психологии мышления [13,14] и некоторые собственные мысли автора по поводу рассмотрения процесса усвоения знаний. Но следует заметить, что человека как носителя информации и накопителя (то есть как субъекта, реализующего процесс усвоения знаний) можно представить как совокупность некоторых биохимических процессов, свойств и взаимодействий. Текущий уровень науки не позволяет разбирать такие процессы на низком биофизическом уровне и позволяет работать лишь с философскими абстракциями. Тем не менее, уже сейчас есть примеры, например [8, 9], где показана принципиальная возможность низкоуровневых исследований процессов усвоения знаний (в данных опытах применялась магнитно-резонансная томография участков мозга, в [9] – для оценки восприятий людьми первичных понятий, в [8] – для оценки последствий усвоенных знаний). Кроме того в современном научном мире есть исследования, подтверждающие влияние на память человека такого процесса, как сон. К сожалению, в России действительно научных исследований на эту тему не проводится и большинство исследований процессов памяти и сна (даже не смотря на существующий в России в Екатеринбурге Клинический Институт Мозга) носят прикладной, а не фундаментальный характер и направлены больше на лечение текущих проблем, например, бессонницы и прочего. Фундаментальные же исследования проводятся в основном за рубежом. Примером таких исследований являются работы [10, 11], в которых показано влияние сна на процесс усвоения знаний. Более того, некоторые известные музыканты, в частности пианисты, говорят о том, что учат произведения во сне. Но в данной работе данная проблема будет описана кратко на основании индийской философии Турьи [12].
Общие понятия о сетях Петри Перед тем как ввести понятие о сетях Петри следует упомянуть о том, что существуют два направления развития сетей Петри. Первое направление – прикладная теория сетей Петри – связана с применением сетей Петри для моделирования систем, их анализа и анализа результатов. Второе направление – чистая теория сетей Петри – занимается разработкой средств, методов и понятий, необходимых для применения сетей Петри [2]. Очевидно, что для задач курсового проекта следует применять прикладную теорию сетей Петри. Но следует помнить, что все они опираются на чистую теорию сетей Петри, которая развивалась множеством авторов, которые, порой, определяли и разрабатывали чистую теорию по разному. В данной работе не будет рассматриваться кратность связей (то есть кратных дуг), но будут использоваться множественные фишка. Подробнее об этих понятиях будет написано ниже. Итак, сеть Петри C является четвёркой Пример сети приведён на рис. 1.
Рис. 1. Пример структуры сети Петри Но визуально удобным является графическое представление сети Петри. Если мы обозначим кружком Граф G сети Петри – это двудольный ориентированный мультиграф, G = (V,A), где Доказательства эквивалентности представлений можно найти в [2], а ниже на рис. 2 приведён рисунок сети рис. 1 в графическом представлении.
Рис. 2. Граф сети Петри, соответствующей сети на рис. 1. Следующим основным понятием, которое мы введём, будет маркировка. Маркировка µ сети Петри – есть отображение множества позиций P в множество неотрицательных целых чисел: За таким понятием скрывается довольно простая вещь – в каждый кружочек мы можем поместить точку (или несколько), которая будет отражать, грубо говоря, некоторый потенциал данной позиции. Например, промаркируем сеть рис. 1 следующим образом: (1, 0, 0, 2, 1). Здесь число, стоящее на i -й позиции в множестве обозначает количество точек в pi. Таким образом мы получаем рис. 3.
Рис. 3. Маркировка сети Петри Следующий пункт – выполнение сети. Для этого надо разобрать исходное понятие – разрешённые переходы. Переход разрешён если каждая из его входных позиций имеет по крайней мере столько фишек, сколько дуг из этой позиции в данный переход. Запуск перехода – перенос фишек через разрешённые переходы из исходных позиций в новые (из исходных позиций фишки удаляются, в новые добавляются). Тогда выполнение сети – процесс запуска переходов. В результате выполнения сети мы получаем новую маркировку µ`. Например, на рис. 3 разрешены переходы t1, t3, t4, а переход t2 запрещён. Переход t1 разрешён потому, что на входе у него позиция p1 с одной дугой и имеет одну фишку. Переход t2 запрещён, так как входящие в него позиции p2 и p3 не имеют фишек вообще. Переход t3 разрешён, так как в него входит посредством двух дуг позиция p4, имеющая 2 фишки. Переход t4 разрешён, так как имеет на входе он имеет позицию p5 с одной фишкой и одной дугой.
Рис. 4. Граф сети после запуска в сети рис.3 перехода t4
Рис. 5. Граф сети после запуска в сети рис.4 перехода t1 Можно заметить, что после последовательного выполнения переходов t4 и t1 переход t2 становится разрешённым. Функция следующего состояния –
Рис. 6. Пример сети Петри для иллюстрации понятия множество достижимости Так как все процессы моделирования усвоения знаний носят вероятностный характер по своей природе, то целесообразно определить стохастическую сеть Петри. Стохастической сетью Петри называется пара Пусть сеть имеет вид, представленный на рис. 7:
Рис. 7. Пример сети И имеет начальную маркировку:
Рис. 8. Маркировка сети рис. 7 Переход t1 разрешён, так как
Рис. 9. Маркировка сети после выполнения перехода t1 Определим вектор r:
Рис. 10. Вектор r Найдём матрицу Грама для векторов
Рис. 11. Матрица Грама Таким образом, маркировка позиции p3 после перехода будет:
Рис. 12. Маркировка позиции p3 после выполнения перехода t1
Применение сетей Петри к задачам моделирования По Питерсону [2], простое представление системы основано на основополагающих понятиях: событиях и условиях. События – это действия, которые имеют место быть в системе. Возникновение событий управляет состоянием системы. Состояние системы, в свою очередь, может быть описано множеством условий. В данном случае условия – это предикаты. Таким образом они могут принимать значения «истина» или «ложь». Так как события являются действиями, то они могут происходить. Чтобы оно произошло должно реализоваться предусловие. Возникновение событий может нарушать предусловия и может привести к выполнению других событий – постусловий. Логичным примером построения простейшей системы с помощью сетей Петри может быть моделирование простого исполнителя, в данном случае – процессора компьютера. С достаточным уровнем абстракции он может быть описан в виде графа сети Петри на рис. 13.
Рис. 13. Моделирование простой вычислительной схемы Следующим важным фактом является тот факт, что выполнение переходов в сети Петри мгновенно. То есть фактор времени здесь не учитывается. Но на деле это не так. Однако зачастую переходами моделируется выполнение каких-либо далеко не мгновенных операций. В этом случае выполнению операции может быть сопоставлен длительный переход. Для наглядности длительные переходы, в отличие от простых, часто обозначаются прямоугольником [5].
Рис. 14. Номенклатура длительного процесса Длительный переход, как и простой, начинает выполнение с изъятия фишек из входных позиций и завершает, соответственно, помещая фишки в выходные. Основное отличие от простого перехода заключается в том, что между этими двумя моментами могут срабатывать другие переходы. Иначе говоря, срабатывание длительного перехода не атомарно. С момента начала выполнения до момента завершения длительный переход считается активным, в противном случае – пассивным. Длительный переход не может сработать, если он активен, т.е. уже выполняется, даже если он разрешен по наличию фишек во входных позициях. Рис. 13 может быть перерисован в следующем виде:
Рис. 15. Использование другой номенклатуры для процесса на рис. 13 Поскольку длительный переход не мгновенен и его срабатывание не атомарно, выполнение различных длительных переходов может перекрываться во времени, т.е. осуществляться параллельно. Длительный переход не мгновенен и его срабатывание не атомарно, выполнение различных длительных переходов может перекрываться во времени, т.е. осуществляться параллельно [5].
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.013 с.) |

 , где
, где 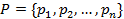 - конечное множество позиций, n > 0,
- конечное множество позиций, n > 0,  - конечное множество переходов, m > 0, таких, что
- конечное множество переходов, m > 0, таких, что  .
.  - является входной функций – отображением из переходов в комплекты позиций.
- является входной функций – отображением из переходов в комплекты позиций.  - выходная функция – отображение из переходов в комплекты позиций [2].
- выходная функция – отображение из переходов в комплекты позиций [2].
 позиции, а палкой | - переходы, а в качестве отображений переходов примем ориентированные стрелки, то получим граф сети Петри.
позиции, а палкой | - переходы, а в качестве отображений переходов примем ориентированные стрелки, то получим граф сети Петри.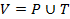 - множество вершин,
- множество вершин,  - комплект направленных дуг,
- комплект направленных дуг,  , где
, где  и для любой направленной дуги либо
и для любой направленной дуги либо  , либо
, либо  .
.
 [2].
[2].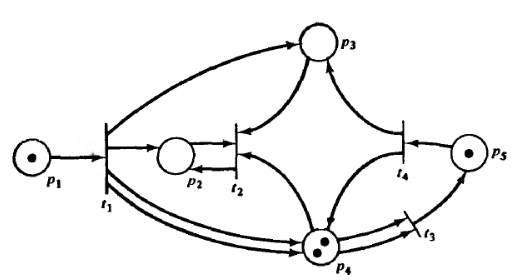


 для сети Петри
для сети Петри  и переходом ti определена тогда и только тогда, когда переход ti разрешён и определяется выражением
и переходом ti определена тогда и только тогда, когда переход ti разрешён и определяется выражением  - где
- где  - новая маркировка, получаемая при выполнении перехода ti. Кроме того следует ввести понятие непосредственно достижимой маркировки. Маркировка
- новая маркировка, получаемая при выполнении перехода ti. Кроме того следует ввести понятие непосредственно достижимой маркировки. Маркировка  такой, что
такой, что  , б) если
, б) если 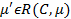 и
и  для некоторого tj
для некоторого tj  Например, для сети на рис. 6. Множеством достижимости R(C, µ) является множество:
Например, для сети на рис. 6. Множеством достижимости R(C, µ) является множество:  [2].
[2].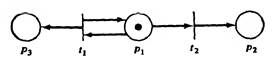
 где
где  , где
, где 
 присваивает каждой позиции вектор распределения вероятности наличия фишек
присваивает каждой позиции вектор распределения вероятности наличия фишек 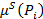 [4]. То есть V – набор векторов, отражающих вероятность нахождения фишки в данной точке. При этом номер компоненты вектора отражает количество фишек, а значение компоненты равняется вероятности нахождения такого количества фишек в этой позиции. Проще говоря, V- двухмерный вектор, первая компонента соответствует номеру позиции, вторая компонента отражает вероятность того, что на данной позиции находится j-е количество фишек. Таким образом, размерность вектора количественно равна произведению количества позиций на максимальное число фишек. Соответственно переход ti в такой сети может быть разрешён тогда и только тогда, когда у вектора вероятностей каждой входной позиции этого перехода имеется компонента, не равная нулю с номером равным или большим числа дуг, соединяющих данную позицию с переходом [4]. Все функции, которые были определены выше для статической сети, теперь носят вероятностный характер. Для описания правил изменения маркировки применяется математический аппарат свёртки матриц Грама.
[4]. То есть V – набор векторов, отражающих вероятность нахождения фишки в данной точке. При этом номер компоненты вектора отражает количество фишек, а значение компоненты равняется вероятности нахождения такого количества фишек в этой позиции. Проще говоря, V- двухмерный вектор, первая компонента соответствует номеру позиции, вторая компонента отражает вероятность того, что на данной позиции находится j-е количество фишек. Таким образом, размерность вектора количественно равна произведению количества позиций на максимальное число фишек. Соответственно переход ti в такой сети может быть разрешён тогда и только тогда, когда у вектора вероятностей каждой входной позиции этого перехода имеется компонента, не равная нулю с номером равным или большим числа дуг, соединяющих данную позицию с переходом [4]. Все функции, которые были определены выше для статической сети, теперь носят вероятностный характер. Для описания правил изменения маркировки применяется математический аппарат свёртки матриц Грама.

 . После срабатывания перехода t1 маркировка позиций p1 и p2 имеет вид:
. После срабатывания перехода t1 маркировка позиций p1 и p2 имеет вид:

 и r:
и r: