
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язання трикутника трилатерації за теоремою Лежандра.Содержание книги
Поиск на нашем сайте
Якщо сферичний трикутник заданий виміряними сторонами і потрібно знайти відповідні сферичні кути, то його розв’язок виконується за теоремою Лежандра наступним способом: 1. Вважаючи сторони сферичного трикутника прямолінійними, розв’язують його за тригонометричними формулами на площині:
де
де
2. Обчислюють сферичний надлишок
3. Обчислюють сферичні кути Розв'язання трикутників за теоремою Лежандра Таблиця 1
Продовження таблиці 1
Приклад розв’язання див. в таблиці 6. Таблиця 2
Розв’язання трикутників за способом аддитаментів. а) нелогарифмічна схема Таблиця 3
180+ б) логарифмічна схема Таблиця 4
180+ Аддитаменти для
Таблиця 5
Розв’язання трикутника трилатерації за теоремою Лежандра. Таблиця 6
Для рішення сферичного трикутника за теоремою Лежандра і способові аддидаментів з використанням програми SfGeodesy, необхідно з меню Создать виконати однойменну команду. Після цієї команди відкриється вікно представлене на рис. 2. Далі необхідно заповнити наступні поля у формі: групу студента; прізвище, ім'я, по батькові студента; кут А; кут В; кут С; сторону b. .
Вихідні дані Таблиця 7
7. Контрольні питання до екзамену з дисципліни
1. Параметри сфероїда обертання 2. Основні системи координат, зв'язок між ними. 3. Головні радіуси кривизни. Нормальні перерізи поверхні еліпсоїда. Середній радіус кривизни. 4. Обчислення довжин дуг меридіанів, паралелей, площин на поверхні еліпсоїда. 5. Обчислення розмірів і площ рамок знімальних трапецій за геодезичними координатами їх кутів. 6. Визначення геодезичних координат кутів рамок трапецій за номенклатурою листів топографічних карт. 7. Геодезична лінія. Зв’язок напрямків геодезичних ліній по слідах прямих та зворотніх нормальних перерізів на поверхні еліпсоїда. 8. Рівняння Клеро. 9. Прямий та зворотній нормальний переріз. Величина розходження. Неоднозначність у побудові трикутників за слідами прямих та зворотних нормальних перерізів. 10. Обчислення геодезичних широт, довгот та азимутів. Загальні положення. Головні геодезичні задачі та методи їх рішення. 11. У чому полягає перевага методу вирішення трикутників за теоремою Лежандра у порівнянні з загальним методом? 12. Призначення аддитаментів. 13. Порядок дій при вирішенні сферичного трикутника загальним методом, за теоремою синусів. 14. Порядок дій при вирішенні трикутника трилатерації за теоремою Лежандра. 15. Рішення прямої геодезичної задачі за способом допоміжної точки (спосіб Красовського). 16. Рішення прямої геодезичної задачі за способом із середніми аргументами. Спосіб Гауса. 17. Рішення зворотної геодезичної задачі за способом Гауса. 18. Методи переобчислення координат Гауса-Крюгера з однієї зони в іншу. 19. Відомості про види проекції еліпсоїда на площину. 20. Рішення прямої та зворотної геодезичної задачі за способом допоміжної сфери (Спосіб Бесселя). 21. Відомості про методи рішення головних геодезичних задач. 22. Які задачі виникають при переході з поверхні еліпсоїда на площину проекції Гауса-Крюгера? 23. Математичні основи проекції Гауса-Крюгера. 24. Обчислення пласких конформних координат Гауса-Крюгера за геодезичними. 25. Обчислення геодезичних координат за координатами Гауса-Крюгера. 26. Редукування трикутника трапеції з еліпсоїда на площину проекції Гауса-Крюгера. 27. зв'язок між геодезичним азимутом і дирекційним кутом проекції Гауса Крюгера. 28. Визначення геодезичних координат за координатами Гауса-Крюгера. 29. Перехід від відстаней на еліпсоїді до відстані на площині в проекції Гауса-Крюгера.
30. Обчислення поправок у напрямки за кривину зображення геодезичної лінії на площині. 31. Формули для визначення Гауссового зближення меридіанів. 32. Визначення масштабу зображення і поправки у відстань при перенесенні його з еліпсоїду на площину. 33. Визначення поправок у напрямки за кривизну зображення геодезичної лінії на площині. 34. Диференційні формули першого і другого роду. Їх призначення. 35. Сформулювати теорему Лежандра. 36. Розв’зання сферичних трикутників за способом Лежандра й аддитаментів.
Рекомендована література 1. Морозов В. П. Курс сфероидической геодезии. Учебник для вузов.-М.: Недра, 1979.-304с. 2. Куштин И. Ф. Геодезия. Учебно-практическое пособие.-М.: "Издательство ПРИОР", 2001.-448с. 3. Куштин И. Ф. Сфероидическая геодезия.: Учебное пособие для вузов.-Ростов-на-Дону, 1982.-110с. 4. Монін І. Ф. Вища геодезія.: Підручник для вузів.-Київ: Наукова думка.-405с. 5. Геодезичний енциклопедичний словник /За редакцієюВолодимира Літинського.-Львів: Євросвіт, 2001.-668с. 6. Савчук С. Г. Вища геодезія/Сфероїдична геодезія.: Підручник.-Львів: Ліга-Прес, 2000.-248с. 7. Беспалов Н.А. Методы решения задач сфероидической геодезии. – М.: Недра 1980 г. 8. Закатов П.С.Курс высшей геодезии. М., Недра. 9. Практикум по высшей геодезии (вычислительные работы)/ Н. В. Яковлев, Н. А. Беспалов, В. П. Глумов и др.: Учебное пособие для вузов. М., Недра, 1982. 368 с.
Додаток А (Зразок титульного листа) Міністерство освіти і науки, молоді та спорту України Державний вищий навчальний заклад «Криворізький національний університет» Кафедра геодезії Контрольна робота З дисципліни _________________________________ Варіант № ______
Виконав (ла): Студент (ка) ____ курсу Групи ___________ ________________________ Прізвище, ініціали № залікової книжки ____________
Перевірив (ла): Доцент _______________________
Кривий Ріг 201_ р. Методичні вказівки до виконання контрольних робіт з дисципліни "Вища геодезія" для студентів 4 курсу напряму підготовки 6.080101“Геодезія, картографія та землеустрій” заочної форми навчання.
Укладачі: Сидоренко Віктор Дмитрович, д.т.н., проф. Перегудов Володимир Володимирович, д.т.н., проф. Мазикіна Ольга Борисівна, к.т.н., доц.
Реєстрац. № ___________
Підписано до друку _____________ 2012 р. Формат А5 Обсяг 24 др. док. Тираж __ прим.
Видавничий центр ДВНЗ «КНУ», вул. ХХІІ партз’їзду, 11, м. Кривий Ріг
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.140.197 (0.01 с.) |

 ,
, ,
, ,
, - площа трикутника,
- площа трикутника, - його півпериметр,
- його півпериметр, ,
, ,
, - виміряні сторони сферичного трикутника,
- виміряні сторони сферичного трикутника, ,
,  ,
,  - кути трикутника на площині.
- кути трикутника на площині.
 ,
,  ,
,  відповідні сторонам заданого сферичного трикутника:
відповідні сторонам заданого сферичного трикутника:
 180 00 04,80
180+
180 00 04,80
180+  180 00 03,78
180 00 03,78
 +1,02
+1,02

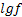 lg f
lg f
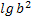

 доп.
доп. 


 ,
,  ,
,  .
.
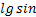 сферичних кутів
сферичних кутів
 сторін плоского трикутника
сторін плоского трикутника
 в 7-ому знаці логарифму.
в 7-ому знаці логарифму.

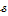 м
м
 м
м
 км
км
 ,
,
 ,
,
 .
.



 =650241
=650241
 =0,00506
=0,00506
 Рис. 2
Рис. 2



