Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’зання сферичних трикутників.Содержание книги Поиск на нашем сайте
Загальні положення Тріангуляція є одним з основних методів визначення взаємного положення точок земної поверхні в плані. Врівноважені на станції напрямки приводяться до центрів знаків і проектуються на поверхню референц-еліпсоїда Красовського шляхом введення поправок за висоту пункту спостереження і за ухилення прямовисних ліній. Довжини початкових сторін (базисів) також переносяться на поверхню еліпсоїда. В результаті напрямки з кожного пункту на суміжні відповідатимуть прямим нормальним перерізам. Після введення в напрями поправок за перехід від нормальних перерізів до геодезичних ліній всі пункти тріангуляції виявляться спроектованими на еліпсоїд, а сторонами тріангуляції - геодезичні лінії. Отримані трикутники формою будуть еліпсоїдними (сферичними). Для обчислення координат пунктів в такій тріангуляції треба розв’язувати сферичні трикутники. Оскільки кривизна поверхні еліпсоїда безперервно змінюється разом з широтою, то розв’язок сферичних трикутників є складною справою. Враховуючи, що полярне стиснення земного еліпсоїда мале, можна очікувати, що кути і сторони сферичного трикутника невеликого розміру мало відрізнятимуться від відповідних кутів і сторін сферичного трикутника, розташованого на сфері, радіус якої дорівнює середньому радіусу кривизни еліпсоїда в центрі заданої області. Так теоретичні дослідження [2] показують: з відносною похибкою в довжині сторін У практиці геодезичних робіт розв’язок трикутника полягає в обчисленні двох його сторін по відомим кутам і стороні. Для цього використовується формула сферичної тригонометрії (теорема синусів)
де Сторони
Рис. 1 У практиці геодезичних обчислень застосовують спеціальні методи вирішення сферичних трикутників, при яких довжини їх сторін в лінійній мірі обчислюються минувши перехід в градусну міру і назад. Таких методів два: 1. Розв’язання трикутників за теоремою Лежандра. 2. Розв’язання трикутників за методом аддитаментів.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.42 (0.006 с.) |

 і кутовий
і кутовий  сферичний трикутник можна розв’язувати як сферичний при довжині сторін
сферичний трикутник можна розв’язувати як сферичний при довжині сторін  км.
км. , (1)
, (1) ,
,  ,
,  ., (2)
., (2) сферичного трикутника
сферичного трикутника  , рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу
, рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу 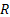 сфери, на якій розташований цей трикутник. Довжини ж сторін
сфери, на якій розташований цей трикутник. Довжини ж сторін  ,
,  ,
,  , отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти
, отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти