

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Рекомендації до самостійного опрацювання окремих тем дисципліни.
Передмова
Методичні вказівки містять перелік тем та питань навчальної програми програми з дисципліни „Вища геодезія”, блок "Сфероїдична геодезія", тематику самостійних та контрольних робіт, а також вимоги до їх оформлення і захисту. Студентам рекомендується вивчати дисципліну відповідно до наведеного навчального плану, використовуючи запропоновану літературу.
1. Перелік тем та питань з дисципліни „Вища геодезія”,
блок "Сфероїдична геодезія"
| № з/п
| Назви тем
| Питання теми
| |
|
|
| | Геометрія Земного еліпсоїда
| |
| Завдання і визначення сфероїдичної геодезії.
| Поняття про загальний земний еліпсоїд, референц елліпсоїд,
Еліпсоїди Красовського, систем координат GRS-80, WGS-84, УСК-2000.
| |
| Основні параметри земного еліпсоїда і співвідношення між ними.
| Розмір земного еліпсоїда. Рівняння поверхні еліпсоїда. Співвідношення між параметрами еліпсоїда.
| |
| Системи координат, що вживаються у вищій геодезії.
| Прямокутні просторові координати. Прямокутні координати на площині. Геодезичні координати. Геоцентричні координати. Система координат з приведеною широтою і геодезичною довготою. Звязок між системами координат.
| |
| Головні і середні радіуси кривин в даній точці еліпсоїда.
| Поняття нормального перерізу, головні нормальні перерізи. Головні радіуси кривин. Середній радіус кривизни, радіус кривизни довільного нормального перерізу.
| |
| Обчислення довжин дуг меридіана та паралелі
| Довжина дуги меридіана. Довжина дуги паралелі.
| |
| Розрахунок рамок і площі знімальних трапецій
| Площа знімальної трапеції. Розрахунок рамок знімальної трапеції.
| |
| Взаємні нормальні перерізи і геодезична лінія
| Взаємні нормальні перерізи. Геодезична лінія. Основне рівняння геодезичної лінії. Розходження між взаємними нормальними перерізами. Довжина дуги нормального перерізу. Кути між взаємними нормальними перерізами і геодезичною лінією. Положення геодезичної лінії відносно взаємних нормальних перерізів.
|
| Розв’язання головних геодезичних задач на поверхні Земного еліпсоїда та у просторі
| |
| Рішення сферичних і сфероїдичних трикутників
| Рішення трикутників за теоремою Лежандра. Рішення трикутників за способом аддитаментів. Рішення великих сфероїдичних трикутників.
| |
| Рішення прямої геодезичної задачі за способом Красовського
| Обчислення елементів трикутника за теоремою Лежандра. Визначення різниці широт даної і допоміжної точок. Визначення різниці довгот між допожіною і шуканою точками. Визначення різниці широт між допоміжною і шуканою точками. Визначення зворотнього азимуту.
| |
| Рішення геодезичної задачі по формулах із середніми аргументами (метод Гаусса)
| Виведення формул шляхом розкладання в ряд різниць широт, довгот і азимутів.
Рішення прямої задачі
Рішення зворотньої задачі.
| |
| Рішення головної геодезичної задачі за способом Бесселя
| Загальні відомості. Виведення диференційних рівнянь. Інтегрування диференційних рівнянь. Порядок обчислень при рішенні прямої і зворотньої задач.
| |
| Рішення головної геодезичної задачі за допомогою нормальних перетинів
| Загальні відомості. Пряма геодезична задача. Зворотня геодезична задача.
| |
| Рішення геодезичних задач у просторі
| Система просторових координат.
Пряма геодезична задача.
Зворотня геодезична задача.
| |
| Аналіз методів, їх точність
| Методи рішення геодезичних задач на малі відстані,
Методи рішення геодезичних задач на середні відстані,
Методи рішення геодезичних задач на великі відстані.
| | Пласкі прямокутні координати Гаусса-Крюгера
| |
| Основні відомості про конформну проекцію Гаусса -Крюгера еліпсоїда на площині.
| Властивості проекції Гаусса-Крюгера. Порядок дій при переході від еліпсоїда на площину в проекції Гаусса-Крюгера. Основні формули.
| |
| Звязок між плоскими координатами x, у в проекції Гаусса-Крюгера і геодезичними координатами B, L
| Формули для визначення конформних плоских координат x, у по геодезичних координатах B, L,
Формули для обчислення геодезичних координат по координатах Гаусса-Крюгера.
|
|
| Зближення меридіанів на площині і масштаб зображення в проекції Гаусса-Крюгера
| Зближення меридіанів на площині у функції геодезичних координат. Зближення меридіанів на площині у функції плоских координат. Формули для обчислення масштабу зображення. Зближення меридіанів. Обчислення зближення меридіанів проекції Гауса-Крюгера.
| |
| Редукування геодезичних вимірювань з еліпсоїда на площину в проекції Гаусса-Крюгера
| Перехід від відстаней на еліпсоїді до відстаней на площині в проекції Гаусса-Крюгера,
Поправки в напрями за кривизну зображення геодезичної лінії на площині,
Редукування трикутника тріангуляції 1 класу з еліпсоїда на площину.
| |
| Перетворення координат Гаусса-Крюгера з однієї зони в іншу, нанесення кілометрової сітки на планшет.
| Умови виникнення необхідності виконати перетворення координат з однієї зони в іншу. Способи перетворення координат з однієї зони в іншу. Виведення формул перетворення координат. Нанесення кілометрової сітки на планшети топографічної зйомки.
|
Зміст завдання
1. Розв’язати трикутник тріангуляції 2 кл.
а) за теоремою Лежандра;
б) за способом аддитаментів.
2. Розв’язати трикутник трилатерації 2 кл. за теоремою Лежандра.
Порядок дій
З таблиці 7 вибрати варіант вихідних даних. Варіант вибирається за номером групи в списку назв вершин і номеру трикутника, який співпадає з порядковим номером студента в журналі групи. Порядок нумерації вершин трикутників для всіх варіантів однаковий і показаний на рис. 1.
Розв’язок трикутника виконується відповідно до завдання, використовуючи семизначні таблиці логарифмів або натуральних значень тригонометричних функцій і керуючись розрахунковими схемами 1, 3, 4, 6 і допоміжними таблицями 2, 5, а також з використанням програми SfGeodesy, яку можна завантажити з такого адреса в мережі інтернет http://sfgeodesy.boom.ru/SfGeodesy.rar.
Загальні положення
Тріангуляція є одним з основних методів визначення взаємного положення точок земної поверхні в плані.
Врівноважені на станції напрямки приводяться до центрів знаків і проектуються на поверхню референц-еліпсоїда Красовського шляхом введення поправок за висоту пункту спостереження і за ухилення прямовисних ліній. Довжини початкових сторін (базисів) також переносяться на поверхню еліпсоїда. В результаті напрямки з кожного пункту на суміжні відповідатимуть прямим нормальним перерізам. Після введення в напрями поправок за перехід від нормальних перерізів до геодезичних ліній всі пункти тріангуляції виявляться спроектованими на еліпсоїд, а сторонами тріангуляції - геодезичні лінії. Отримані трикутники формою будуть еліпсоїдними (сферичними).
Для обчислення координат пунктів в такій тріангуляції треба розв’язувати сферичні трикутники. Оскільки кривизна поверхні еліпсоїда безперервно змінюється разом з широтою, то розв’язок сферичних трикутників є складною справою.
Враховуючи, що полярне стиснення земного еліпсоїда мале, можна очікувати, що кути і сторони сферичного трикутника невеликого розміру мало відрізнятимуться від відповідних кутів і сторін сферичного трикутника, розташованого на сфері, радіус якої дорівнює середньому радіусу кривизни еліпсоїда в центрі заданої області.
Так теоретичні дослідження [2] показують: з відносною похибкою в довжині сторін  і кутовий і кутовий  сферичний трикутник можна розв’язувати як сферичний при довжині сторін сферичний трикутник можна розв’язувати як сферичний при довжині сторін  км. км.
У практиці геодезичних робіт розв’язок трикутника полягає в обчисленні двох його сторін по відомим кутам і стороні. Для цього використовується формула сферичної тригонометрії (теорема синусів)
 , (1) , (1)
де  , ,  , ,  ., (2) ., (2)
Сторони  сферичного трикутника сферичного трикутника  , рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу , рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу 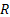 сфери, на якій розташований цей трикутник. Довжини ж сторін сфери, на якій розташований цей трикутник. Довжини ж сторін  , ,  , ,  , отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти , отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти  за формулами (2), потім синуси цих сторін і після розв’язку виконати перехід в лінійну міру. Тобто вирішення сферичних трикутників по звичайній схемі вимагає додаткових обчислень в порівнянні з вирішенням трикутників на площині. за формулами (2), потім синуси цих сторін і після розв’язку виконати перехід в лінійну міру. Тобто вирішення сферичних трикутників по звичайній схемі вимагає додаткових обчислень в порівнянні з вирішенням трикутників на площині.
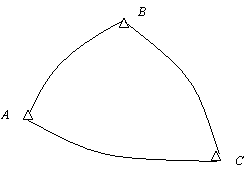
Рис. 1
У практиці геодезичних обчислень застосовують спеціальні методи вирішення сферичних трикутників, при яких довжини їх сторін в лінійній мірі обчислюються минувши перехід в градусну міру і назад. Таких методів два:
1. Розв’язання трикутників за теоремою Лежандра.
2. Розв’язання трикутників за методом аддитаментів.
Вихідні дані
Таблиця 7
| | № тр-ка
| Назва вершин
| Виміряні кути
| Геодезичні координати п. А, азимут сторони, логарифм сторони
| | | I
| II
| III
| IV
| | |
|
|
|
|
|
|
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 56˚38΄28,˝30
66 32 49,08
56 48 44,90
| В =45˚42΄33,˝585
L =25 48 32,275
А АВ =32 39 18,175
lg S =4.435 8622
S АС =27 281,120
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 55˚28 25,18
64˚37 48,67
59˚53 47,85
| В =45 20 32,175
L =24 32 30,221
А АС =121 31 18,240
lg S =4.408 1275
S АВ =25 593,372
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 55 16 23,28
62 44 08,32
61 59 32,02
| В =45 23 48,240
L =26 31 38,451
А AC =108 35 21,710
lg S =4.410 3145
S AB =25 722,578
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 59 16 20,70
60 46 10,42
59 57 30,75
| В = 46 13 21,531
L = 28 20 51,275
А АВ = 86 15 25,380
lg S =4.405,2885
S АС =25 426,612
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 58 18 18,41
60 45 12,71
60 56 30,84
| В= 46 21 20,635
L =28 21 52,348
А АВ =80 26 32,780
lg S =4.408 2028
S АС =25 597,809
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 60°30΄22˝,11
56 30 22,80
62 59 19,01
| В =46°44΄18˝,125
L =27 28 36,785
А АВ =73 28 38,248
lg S =4.418 2211
S АС =26 195,162
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 60 42 49,18
64 28 27,92
58 48 44,80
| В =46 43 46,395
L =15 48 32,456
А АВ =40 36 21,112
lg S =4.425 8654
S АС =26 660,323
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 58 01 00,10
65 33 40,92
56 25 20,140
| В =46 23 35,264
L =11 53 00,230
А АВ =170 24 37,025
lg S =4.415 8245
S АС =26 051,006
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 67 56 33,61
56 38 20,76
55 25 07 25
| В =46 20 48,325
L =17 53 01,208
А АВ =49 17 55,147
lg S =4.382 5612
S АС =24 297,478
| |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 63 26 08,61
61 34 11,05
54 59 41,57
| В =46 12 54,315
L =23 55 18,154
А АВ =41 20 21,132
lg S =4.396 2678
S АС =24 903,925
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 70 18 34,75
54 14 30,63
55 26 57,04
| В =47 32 18,1020
L =29 47 10,324
А АС =245 17 15,250
lg S =4.428 2438
S АВ =26 806,728
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 60°30΄22˝,11
56 30 22,80
62 59 19,01
| В =46°44΄18˝,125
L =27 28 36,785
А АВ =73 28 38,248
lg S =4.418 2211
S АС =26 195,163
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 62 35 58,25
59 36 35,29
57 47 26,03
| В =47 02 11,035
L =31 56 25,186
А АВ =54 38 45,768
lg S =4.502 4826
S АС =31 804,063
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 61 02 54,38
57 14 50,76
61 42 15,78
| В =45 42 12,542
L =47 56 02,246
А АВ =85 38 14,246
lg S =4.549 8462
S АС =35 468,776
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 63 32 47,89
55 38 44,94
60 48 29,22
| В =45 27 37,654
L =23 42 56,245
А АВ =245 25 36,264
lg S =4.429 8222
S =26 904,331
АС
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 53 52 44,71
60 48 05,28
65 19 10,12
| В =45 38 12,201
L =59 44 56,754
А АС =265 38 42,567
lg S =4.401 2615
S АВ =25 191,933
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 66 42 39,02
54 28 37,15
58 48 45,65
| В =47 25 13,542
L =42 14 15,587
А АС =352 21 45,652
lg S =4.425 8674
S АВ =26 660,445
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 68°11΄25˝,56
55 23 08,56
56 25 25,42
| В =46°38΄42˝,657
L =41 47 31,128
А АС =164 54 26,438
lg S =4.506 8765
S АВ = 32 127,468
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 62 42 18,24
60 12 42,04
57 04 59,42
| В =47 08 42,1425
L =35 24 45,452
А АС =75 42 31,076
lg S =4.498 1456
S АВ =31 488,038
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 65 10 34,50
55 01 14,54
59 48 13,08
| В =47 42 11,657
L =24 54 18,452
А АВ =82 31 45,142
lg S =4.576 2415
S АС =37 691,333
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 66 15 15,98
58 44 50,45
54 59 57,07
| В =46 54 27,568
L =42 11 54,264
А АВ =262 14 52,675
lg S =4.566 4521
S АС =36 851,240
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 60 25 31,21
50 05 14,80
69 29 14,45
| В =47 07 24,786
L =42 54 12,425
А АВ =76 42 36,765
lg S =4.486 5268
S АС =30 656,799
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 64 42 11,54
61 42 08,11
53 35 40,01
| В =46 42 27,768
L =34 41 52,142
А АС =165 24 19,654
lg S =4.454 1456
S АВ =28 454,149
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 59°21΄16˝,42
56 45 40,14
63 53 02,65
| В =47°45΄24˝,542
L =42 54 11,245
А АС =64 24 11,421
lg S =4.410 1542
S АВ =25 713,086
| | |
| А
С
В
| В
А
С
| С
В
А
| А
В
С
| 68 42 11,45
62 18 21,50
48 59 27,11
| В =47 10 24,426
L =30 45 12,412
А АС =125 41 30,165
lg S =4.510 4218
S АВ =32 390,809
| | | | | | | | | | | | | | | | | |
7. Контрольні питання до екзамену з дисципліни
1. Параметри сфероїда обертання
2. Основні системи координат, зв'язок між ними.
3. Головні радіуси кривизни. Нормальні перерізи поверхні еліпсоїда. Середній радіус кривизни.
4. Обчислення довжин дуг меридіанів, паралелей, площин на поверхні еліпсоїда.
5. Обчислення розмірів і площ рамок знімальних трапецій за геодезичними координатами їх кутів.
6. Визначення геодезичних координат кутів рамок трапецій за номенклатурою листів топографічних карт.
7. Геодезична лінія. Зв’язок напрямків геодезичних ліній по слідах прямих та зворотніх нормальних перерізів на поверхні еліпсоїда.
8. Рівняння Клеро.
9. Прямий та зворотній нормальний переріз. Величина розходження. Неоднозначність у побудові трикутників за слідами прямих та зворотних нормальних перерізів.
10. Обчислення геодезичних широт, довгот та азимутів. Загальні положення. Головні геодезичні задачі та методи їх рішення.
11. У чому полягає перевага методу вирішення трикутників за теоремою Лежандра у порівнянні з загальним методом?
12. Призначення аддитаментів.
13. Порядок дій при вирішенні сферичного трикутника загальним методом, за теоремою синусів.
14. Порядок дій при вирішенні трикутника трилатерації за теоремою Лежандра.
15. Рішення прямої геодезичної задачі за способом допоміжної точки (спосіб Красовського).
16. Рішення прямої геодезичної задачі за способом із середніми аргументами. Спосіб Гауса.
17. Рішення зворотної геодезичної задачі за способом Гауса.
18. Методи переобчислення координат Гауса-Крюгера з однієї зони в іншу.
19. Відомості про види проекції еліпсоїда на площину.
20. Рішення прямої та зворотної геодезичної задачі за способом допоміжної сфери (Спосіб Бесселя).
21. Відомості про методи рішення головних геодезичних задач.
22. Які задачі виникають при переході з поверхні еліпсоїда на площину проекції Гауса-Крюгера?
23. Математичні основи проекції Гауса-Крюгера.
24. Обчислення пласких конформних координат Гауса-Крюгера за геодезичними.
25. Обчислення геодезичних координат за координатами Гауса-Крюгера.
26. Редукування трикутника трапеції з еліпсоїда на площину проекції Гауса-Крюгера.
27. зв'язок між геодезичним азимутом і дирекційним кутом проекції Гауса Крюгера.
28. Визначення геодезичних координат за координатами Гауса-Крюгера.
29. Перехід від відстаней на еліпсоїді до відстані на площині в проекції Гауса-Крюгера.
30. Обчислення поправок у напрямки за кривину зображення геодезичної лінії на площині.
31. Формули для визначення Гауссового зближення меридіанів.
32. Визначення масштабу зображення і поправки у відстань при перенесенні його з еліпсоїду на площину.
33. Визначення поправок у напрямки за кривизну зображення геодезичної лінії на площині.
34. Диференційні формули першого і другого роду. Їх призначення.
35. Сформулювати теорему Лежандра.
36. Розв’зання сферичних трикутників за способом Лежандра й аддитаментів.
Рекомендована література
1. Морозов В. П. Курс сфероидической геодезии. Учебник для вузов.-М.: Недра, 1979.-304с.
2. Куштин И. Ф. Геодезия. Учебно-практическое пособие.-М.: "Издательство ПРИОР", 2001.-448с.
3. Куштин И. Ф. Сфероидическая геодезия.: Учебное пособие для вузов.-Ростов-на-Дону, 1982.-110с.
4. Монін І. Ф. Вища геодезія.: Підручник для вузів.-Київ: Наукова думка.-405с.
5. Геодезичний енциклопедичний словник /За редакцієюВолодимира Літинського.-Львів: Євросвіт, 2001.-668с.
6. Савчук С. Г. Вища геодезія/Сфероїдична геодезія.: Підручник.-Львів: Ліга-Прес, 2000.-248с.
7. Беспалов Н.А. Методы решения задач сфероидической геодезии. – М.: Недра 1980 г.
8. Закатов П.С.Курс высшей геодезии. М., Недра.
9. Практикум по высшей геодезии (вычислительные работы)/ Н. В. Яковлев, Н. А. Беспалов, В. П. Глумов и др.: Учебное пособие для вузов. М., Недра, 1982. 368 с.
Додаток А
(Зразок титульного листа)
Міністерство освіти і науки, молоді та спорту України
Державний вищий навчальний заклад
«Криворізький національний університет»
Кафедра геодезії
Контрольна робота
З дисципліни _________________________________
Варіант № ______
Виконав (ла):
Студент (ка) ____ курсу
Групи ___________
________________________
Прізвище, ініціали
№ залікової книжки ____________
Перевірив (ла):
Доцент _______________________
Кривий Ріг
201_ р.
Методичні вказівки до виконання контрольних робіт з дисципліни "Вища геодезія" для студентів 4 курсу напряму підготовки 6.080101“Геодезія, картографія та землеустрій” заочної форми навчання.
Укладачі:
Сидоренко Віктор Дмитрович, д.т.н., проф.
Перегудов Володимир Володимирович, д.т.н., проф.
Мазикіна Ольга Борисівна, к.т.н., доц.
Реєстрац. № ___________
Підписано до друку _____________ 2012 р.
Формат А5
Обсяг 24 др. док.
Тираж __ прим.
Видавничий центр ДВНЗ «КНУ»,
вул. ХХІІ партз’їзду, 11,
м. Кривий Ріг
Передмова
Методичні вказівки містять перелік тем та питань навчальної програми програми з дисципліни „Вища геодезія”, блок "Сфероїдична геодезія", тематику самостійних та контрольних робіт, а також вимоги до їх оформлення і захисту. Студентам рекомендується вивчати дисципліну відповідно до наведеного навчального плану, використовуючи запропоновану літературу.
1. Перелік тем та питань з дисципліни „Вища геодезія”,
блок "Сфероїдична геодезія"
| № з/п
| Назви тем
| Питання теми
| |
|
|
| | Геометрія Земного еліпсоїда
| |
| Завдання і визначення сфероїдичної геодезії.
| Поняття про загальний земний еліпсоїд, референц елліпсоїд,
Еліпсоїди Красовського, систем координат GRS-80, WGS-84, УСК-2000.
| |
| Основні параметри земного еліпсоїда і співвідношення між ними.
| Розмір земного еліпсоїда. Рівняння поверхні еліпсоїда. Співвідношення між параметрами еліпсоїда.
| |
| Системи координат, що вживаються у вищій геодезії.
| Прямокутні просторові координати. Прямокутні координати на площині. Геодезичні координати. Геоцентричні координати. Система координат з приведеною широтою і геодезичною довготою. Звязок між системами координат.
| |
| Головні і середні радіуси кривин в даній точці еліпсоїда.
| Поняття нормального перерізу, головні нормальні перерізи. Головні радіуси кривин. Середній радіус кривизни, радіус кривизни довільного нормального перерізу.
| |
| Обчислення довжин дуг меридіана та паралелі
| Довжина дуги меридіана. Довжина дуги паралелі.
| |
| Розрахунок рамок і площі знімальних трапецій
| Площа знімальної трапеції. Розрахунок рамок знімальної трапеції.
| |
| Взаємні нормальні перерізи і геодезична лінія
| Взаємні нормальні перерізи. Геодезична лінія. Основне рівняння геодезичної лінії. Розходження між взаємними нормальними перерізами. Довжина дуги нормального перерізу. Кути між взаємними нормальними перерізами і геодезичною лінією. Положення геодезичної лінії відносно взаємних нормальних перерізів.
|
| Розв’язання головних геодезичних задач на поверхні Земного еліпсоїда та у просторі
| |
| Рішення сферичних і сфероїдичних трикутників
| Рішення трикутників за теоремою Лежандра. Рішення трикутників за способом аддитаментів. Рішення великих сфероїдичних трикутників.
| |
| Рішення прямої геодезичної задачі за способом Красовського
| Обчислення елементів трикутника за теоремою Лежандра. Визначення різниці широт даної і допоміжної точок. Визначення різниці довгот між допожіною і шуканою точками. Визначення різниці широт між допоміжною і шуканою точками. Визначення зворотнього азимуту.
| |
| Рішення геодезичної задачі по формулах із середніми аргументами (метод Гаусса)
| Виведення формул шляхом розкладання в ряд різниць широт, довгот і азимутів.
Рішення прямої задачі
Рішення зворотньої задачі.
| |
| Рішення головної геодезичної задачі за способом Бесселя
| Загальні відомості. Виведення диференційних рівнянь. Інтегрування диференційних рівнянь. Порядок обчислень при рішенні прямої і зворотньої задач.
| |
| Рішення головної геодезичної задачі за допомогою нормальних перетинів
| Загальні відомості. Пряма геодезична задача. Зворотня геодезична задача.
| |
| Рішення геодезичних задач у просторі
| Система просторових координат.
Пряма геодезична задача.
Зворотня геодезична задача.
| |
| Аналіз методів, їх точність
| Методи рішення геодезичних задач на малі відстані,
Методи рішення геодезичних задач на середні відстані,
Методи рішення геодезичних задач на великі відстані.
| | Пласкі прямокутні координати Гаусса-Крюгера
| |
| Основні відомості про конформну проекцію Гаусса -Крюгера еліпсоїда на площині.
| Властивості проекції Гаусса-Крюгера. Порядок дій при переході від еліпсоїда на площину в проекції Гаусса-Крюгера. Основні формули.
| |
| Звязок між плоскими координатами x, у в проекції Гаусса-Крюгера і геодезичними координатами B, L
| Формули для визначення конформних плоских координат x, у по геодезичних координатах B, L,
Формули для обчислення геодезичних координат по координатах Гаусса-Крюгера.
|
|
| Зближення меридіанів на площині і масштаб зображення в проекції Гаусса-Крюгера
| Зближення меридіанів на площині у функції геодезичних координат. Зближення меридіанів на площині у функції плоских координат. Формули для обчислення масштабу зображення. Зближення меридіанів. Обчислення зближення меридіанів проекції Гауса-Крюгера.
| |
| Редукування геодезичних вимірювань з еліпсоїда на площину в проекції Гаусса-Крюгера
| Перехід від відстаней на еліпсоїді до відстаней на площині в проекції Гаусса-Крюгера,
Поправки в напрями за кривизну зображення геодезичної лінії на площині,
Редукування трикутника тріангуляції 1 класу з еліпсоїда на площину.
| |
| Перетворення координат Гаусса-Крюгера з однієї зони в іншу, нанесення кілометрової сітки на планшет.
| Умови виникнення необхідності виконати перетворення координат з однієї зони в іншу. Способи перетворення координат з однієї зони в іншу. Виведення формул перетворення координат. Нанесення кілометрової сітки на планшети топографічної зйомки.
|
Рекомендації до самостійного опрацювання окремих тем дисципліни.
Самостійна робота є важливою часткою навчального процесу студентів і потребує від них відповідальності, сумлінності та зосередженості при вивченні дисципліни, особливо за заочною формою навчання, що передбачає перш за все зменшення аудиторного часу занять та збільшення годин на самостійне опрацювання матеріалу.
Методика самостійної роботи передбачає ведення конспекту, в якому фіксують основні і головні положення матеріалу, що вивчається.
Результатом самостійної роботи може також стати складання реферату на відповідну тему, користуючись багатьма джерелами інформації. При самостійному опанування тем слід користуватися підручниками, перелік яких наведений у списку рекомендованої літератури.
|



 і кутовий
і кутовий  сферичний трикутник можна розв’язувати як сферичний при довжині сторін
сферичний трикутник можна розв’язувати як сферичний при довжині сторін  км.
км. , (1)
, (1) ,
,  ,
,  ., (2)
., (2) сферичного трикутника
сферичного трикутника  , рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу
, рис. 1, як дуги великих кругів повинні бути виражені в частинах радіусу 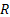 сфери, на якій розташований цей трикутник. Довжини ж сторін
сфери, на якій розташований цей трикутник. Довжини ж сторін  ,
,  ,
,  , отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти
, отримані з вимірювань, виражаються в лінійній мірі. Отже, при розв’язку трикутника за формулою (1) треба спочатку знайти 



