Дослідження оптимального приймача бінарних сигналів.

 

Мета роботи: Досліджувати властивості, характеристики і параметри оптимального приймача бінарних сигналів.

Завдання роботи:

1. Вивчити алгоритм обробки бінарних сигналів в оптимальному приймачі.

2. Вивчити робочі характеристики оптимального приймача.

3. Вивчити вплив лінії зв'язку на роботу оптимального приймача бінарних сигналів.

 

ВВЕДЕННЯ.

Окремим випадком дискретних сигналів є сигнали бінарні, приймаючі одне з двох можливих значень (0,1 або -1,+1). Прийом бінарних сигналів в шумах є одній з важливих проблем, що вирішуються в теорії електрозв'язку. На вирішенні цієї проблеми засновано багато методів оптимальної обробки сигналів в цифрових системах зв'язку.

Бінарний сигнал може бути представлений у вигляді

 

де

 

ступінчаста функція

 

тривалість елементарної бінарної посилки сигналу

, інформаційний параметр бінарного сигналу, що представляє в даному випадку послідовність значень

, амплітуда передаваних імпульсів.

Оптимальний приймач, структурна схема якого приведена на мал. 1, є пристроєм, що здійснює когерентну обробку імпульсної послідовності, що поступає, з використанням інформації про моменти зміни передаваного бінарного сигналу. Ця обробка включає інтеграцію сигналу протягом часу і порівнянні отриманого результату інтеграції із заданим порогом. Вхідним сигналом приймача є аддитивна суміш

 

де - Гаусів білий шум.

 

 

Приймач оптимальний в сенсі мінімуму середньої вірогідності помилкових рішень, що отримуються при обробці кожного інформаційного біта, що поступає на його вхід. Середня вірогідність помилкового рішення буде рівна

 

де - функція Гауса

- відношення енергії на біт до спектральної щільності шуму.

 

Як видно з приведеної формули, є тільки функцією від співвідношення енергій на біт сигналу і шуму. Ця залежність є одному з різновидів характеристик, використовуваних для оцінки якості прийому дискретних сигналів в шумах і званих робочими характеристиками приймача (РХП).

 

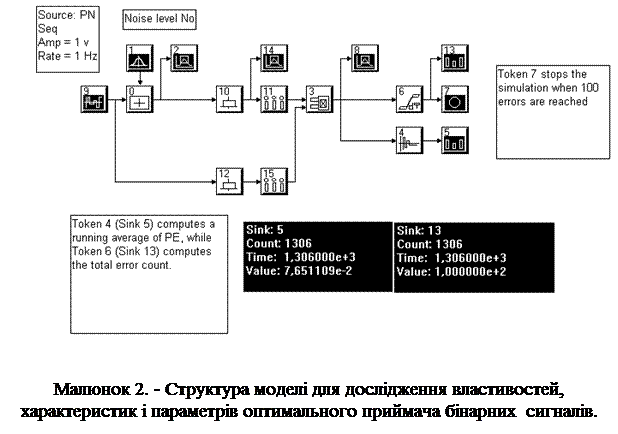
ПОСТАНОВКА ЗАВДАНЬ ДОСЛІДЖЕННЯ.

У даному дослідженні робота оптимального приймача відтворюється моделлю, структура якої приведена на мал. 2. Джерело 9 генерує випадкову бінарну послідовність, з якою змішується Гаусів білий шум, що поступає від джерела 1. Ця суміш обробляється модулем 10, що здійснює ковзаюче усереднювання на інтервалі. Дискретизація сигналу, що проінтегрував, за часом здійснюється модулем 11, порівняння з порогом - модулем 3. Модулі 12 і 15 відтворюють роботу такого ж приймача, але оброблювального імпульсну послідовність без шумів, а, отже, і без помилок при ухваленні рішень. Цей приймач використовується як еталонний по відношенню до досліджуваного при оцінці правильності ухвалення рішень. Для отримання оцінок вірогідності помилкових рішень в даній роботі використовується метод статистичних випробувань (метод Монте-Карло), що передбачає накопичення і обробку статистичних даних при обробці приймачем, випадковій бінарній послідовності, що поступає на його вхід. Результати обробки кожного приймача біта (ухвалене рішення), що поступив на вхід, оцінюється на предмет правильності або помилковості, підсумовуються з результатом попередніх оцінок і ця сума ділиться на число оброблених біт. При необмеженому збільшенні числа оброблюваних біт, отримане відношення сходиться по вірогідності до відповідної вірогідності (у нашому випадку - середній вірогідності помилкових рішень). Процес моделювання закінчується досягши заданого порогового числа аналізованих подій (у нашому випадку - помилок в ухваленні рішень).

У даній роботі передбачається аналіз процесів обробки сигналів в приймачі (на основі зіставлення графіків сигналів в нім з відповідними графіками для еталонного приймача). Крім того, планом роботи передбачено експериментальне отримання РХП і порівняння її з теоретичною, дослідження роботи приймача при включенні на його вході лінії зв'язку, що вносить затримку і що обмежує спектр сигналу і шуму, отримання РХП для цих випадків.

 

ПЛАН ВИКОНАННЯ РОБОТИ.

1. Завантажити виконуючий файл com_bbb.svu (Ріс.2). Увійти в Help пакету, вивчити функції і параметри модулів 3,4,5,6,7,9,10,11. Дати опис функцій і параметрів цих модулів.

Доповнити модель аналізуючими модулями для реєстрації вихідних сигналів модулів 9, 11,12,15. Змінити частоту дискретизації при моделюванні з 1 Гц на 10 Гц. Записати параметри модулів і системного часу.

 

Запустити модель на цикл моделювання і отримати графіки величин, що характеризують роботу оптимального приймача за наявності і відсутності перешкод. Для поліпшення дозволу за часом необхідно змінити масштаб відповідних аналізуючих вікон так, що б на екран виводився відрізок реалізації довжиною 30-50с. Порівняти графіки відповідних величин для випадку наявності перешкод і їх відсутності і дати пояснення відмінностям.

1. Отримати графік сигналу на виході модуля 3. Пояснити його формування на основі аналізу вхідних сигналів цього модуля і функції, що реалізовується модулем.

2. Пояснити поведінку кривих на графіках залежностей, що реєструються модулями 5 і 13. Дати пояснення величинам, представлених на цих графіках на момент закінчення моделювання. Порівняти значення цих величин із значеннями, що виводяться на транспаранти (Sink 5, Sink 13) структурної схеми моделі.

Задавшись рядом значень спектральної щільності шуму (5-6 крапок в інтервалі 0.5-8 вт/гц) і змінюючи тим самим відношення энергии-на-бит до спектральної щільності шуму, побудувати графік вірогідності помилкового прийому від величини цього відношення (РХП). Для підвищення достовірності результатів необхідно збільшити максимальне число відліків при моделюванні до 200000 (Sys.

 

1. Time) і порогове значення помилок для закінчення моделювання до 1000 (модуль 7). Оцінити повторюваність результатів.

2. Отримати спектр передаваної імпульсної послідовності. Встановити на вході приймача (модуль 10) ФНЧ Бесселя 9-го порядку з частотою зрізу, відповідною третьому мінімуму в спектрі передаваного сигналу. Цей фільтр моделюватиме недосконалу лінію зв'язку, що обмежує спектр сигналу. Визначити затримку, що вноситься фільтром. Для її компенсації на вході еталонного приймача (модуль 12) встановити елемент затримки з необхідною велічиной затримки.

3. Виконати п.2 «Плану виконання роботи».

4. Виконати п.6 «Плану виконання роботи» і порівняти отримані результати з результатами п.8. Дати обгрунтування спостережуваним відмінностям.

5. Побудувати графік теоретичної РХП, обчисленої для використаних в п.6 значень спектральної щільності шуму. Порівняти отриманий графік з результатами п.6.

6. ЗМІСТ ЗВІТУ.

7. 1. Найменування роботи, її мета і завдання.

8. 2. Структурна схема моделей, їх параметри, параметри системного часу.

9. 3. Ескізи графіків сигналів, їх спектрів побудови залежності і

10. обчислення значення параметрів відповідно до пункту 1-10 "Плану виконання роботи".

11. 4. Виводи відповідно до пунктів 1-10 "Плану виконання роботи".

12.

13. ЛІТЕРАТУРА.

14. 1. Фельдбаум А..а. і ін. Теоретичні основи зв'язку і управління.

15. 2. Зюко а.Г. і ін. Теорія передачі сигналів.

16.

17. ДОДАТКОВЕ ЗАВДАННЯ.

18.

19. Запропонувати і обгрунтувати структурну схему моделі для дослідження впливу енергії шуму на вірогідності помилкового прийому "1" і пропуску "1" (Вірогідність помилок типу "помилкова тривога" і "пропуск сигналу") при прийомі дискретних сигналів оптимальним приймачем.