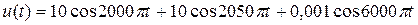Цифровий частотний аналіз полігармонічних сигналів

ЛАБОРАТОРНА РОБОТА №1

 

ЛАБОРАТОРНА РОБОТА №2

 

ЛАБОРАТОРНА РОБОТА №3

 

ЛАБОРАТОРНА РОБОТА №4

 

ЛАБОРАТОРНА РОБОТА №6.

 

ЛАБОРАТОРНА РОБОТА №7.

 

ЛАБОРАТОРНА РОБОТА №8

 

ЛАБОРАТОРНА РОБОТА №9

 

ЛАБОРАТОРНА РОБОТА №10

 

 

ЛАБОРАТОРНА РОБОТА №11

 

 

ЛАБОРАТОРНА РОБОТА №1

 

ЦИФРОВИЙ ЧАСТОТНИЙ АНАЛІЗ ПОЛІГАРМОНІЧНИХ СИГНАЛІВ

 

Мета роботи: Вивчити методи частотного аналізу полігармонічних сигналів.

Завдання роботи:

Ознайомитися з методами і технікою оцінки амплітуди і частоти компонент полігармонічних сигналів.

2. Досліджувати явище «витоку» при цифровому частотному аналізі і його вплив на достовірність отримуваних результатів.

3. Досліджувати вплив перешкод на результати оцінки параметрів полігармонічних сигналів.

4. Вивчити методи підвищення точності оцінки частоти і амплітуди гармонійних компонент сигналу при частотному аналізі.

ВВЕДЕННЯ

 

Цифрові засоби широко застосовуються в техніці зв'язку для обробки сигналів і оцінки параметрів останніх. Їх застосування дозволяє істотно підвищити якість роботи систем. Проте застосування цифрових методів мають деякі особливості порівняно з традиційними аналоговими методами, які необхідно знати для отримання достовірних результатів і правильної їх інтерпретації. Зокрема, слідує правильно і обгрунтовано задавати тривалість досліджуваної реалізації, параметри тимчасової дискретизації, динамічний діапазон, вид використовуваної шкали для представлення результатів. Крім того, слід брати до уваги деякі специфічні ефекти, що мають місце в цифрових системах пов'язаних з обробкою вибірок кінцевого об'єму, обмеженим динамічним діапазоном, впливом шумів.

Дана робота направлена на вивчення вказаних питань засобами пакету System View.

ПОСТАНОВКА ЗАВДАНЬ ДОСЛІДЖЕННЯ

Об'єктом дослідження є полігармонічний сигнал вигляду

 

визначений на обмеженому інтервалі , і що має в своєму складі n компонент з амплітудами і частотами f .

Гармонійні компоненти можуть мати близькі частоти і значну відмінність в амплітудах. Крім того, тривалість відрізання досліджуваного сигналу може виявитися недостатньою для отримання надійних оцінок параметрів, а дуже велика тривалість зажадає великого об'єму пам'яті ЕОМ і часу на обробку. Раціональні завдання параметрів вибірки і налаштувань аналізуючих вікон дозволяє найефективніше вирішити задачу частотного аналізу.

У даній лабораторній роботі досліджуваним сигналом є трикомпонентний полігармонічний сигнал

 

По ходу роботи деякі параметри цього сигналу можуть змінюватися, і в його склад може бути введена додаткова компоненту у вигляді Гауссова випадкового процесу. Завдання даної лабораторної роботи реалізуються шляхом вибору відповідного набору засобів обробки, раціонального завдання їх параметрів, а так само параметрів візуалізація, що забезпечує якнайкращі результати оцінки.

ХІД ВИКОНАННЯ РОБОТИ

1. Завантажити виконуючий файл dsp_wind.svu (ріс.1). Замалювати структуру моделі, записати параметри її модулів, параметри системного часу. Порівняти ці параметри з параметрами наведеного вище трикомпонентного полігармонічного сигналу.

 

 

 

Запустити модель на цикл моделювання. Отримати графіки вихідного сигналу (Sink4) і його спектру. Використовуючи переміщуваний «мишею» курсор і поле індикації його координат (область правого верхнього кута меню аналізу), оцінити характерні величини представлення сигналів в аналізуючих вікнах (max, min значення, амплітуди, частоти, тривалість). Порівняти отримані результати з параметрами ідеального сигналу. Відзначити вплив «витоку» енергії одних спектральних компонент сигналу на сусідніх і її вплив на достовірність результатів. Зробити виводи щодо можливості і достовірності оцінки параметрів досліджуваного сигналу.

1. Піддати тимчасову реалізацію сигналу «зважуванню» (windowing) з використанням стандартних вікон Барлетта (Barlett), Ханнінга (Hanning), Еланикс (Elanix). Для кожного випадку отримати спектр «зваженого» сигналу. Провести оцінку параметрів амплітуди і частоти кожній з компонент сигналу для кожного випадку. Виконати ескізи графіків спектрів з вказівкою отриманих оцінок. Порівняти отримані результати з параметрами ідеального сигналу. Зробити виводи щодо можливості і достовірності оцінки параметрів при використанні тимчасових вікон, що «зважують».

2. Ввести до складу сигналу аддитивний Гаусів шум, шляхом доповнення джерел ще одним - джерелом Гауссова шуму з математичним очікуванням (mean) рівним 0 і середньоквадратичним відхиленням (Std Deviation) рівним 0,0003в. Отримати графік спектру з використанням вікна Ханнінга. Отримати оцінки частоти і амплітуди для кожної спектральної компоненти. Оскільки перешкода носить випадковий характер, слід повторити цикл моделювання і отримання оцінок сигналу багато разів (не менше 5-ти разів), а шукані оцінки знаходити як середні величини прочитуваних значень оцінюваних параметрів для кожного циклу моделювання. Повторити наведену вище послідовність отримання оцінок параметра сигналу для значень середньоквадратичного відхилення 0,001в і 0,003в. Зробити графік спектру сигналу для першого циклу моделювання з вказівкою на нім оцінок параметра сигналу, отриманих для всіх трьох циклів. Зробити виводи щодо впливу перешкод на можливість і достовірність оцінок параметрів сигналу.

3. Відновити початкову структуру і параметри моделі (Див. п.1). Викликати панель налаштувань системного часу і встановити число циклів моделювання (№ of System Loops) рівним 10. Виконати пункт 2 дані «Ходи виконання роботи» при нових налаштуваннях. Зробити виводи щодо можливості отримання оцінок параметрів сигналу і їх достовірності. Виконати пункт 3 даний

 

«Ходу виконання роботи» (використовувати тільки вікно Еланикс). Зробити виводи щодо можливості отримання оцінок параметрів сигналу і їх достовірності.

1. ЗМІСТ ЗВІТУ

2. Найменування роботи, її мета і завдання.

3. Структура моделі, її параметри, параметри системного часу.

4. Ескізи графіків сигналів, їх спектрів з вказівкою отриманих оцінок параметрів, а так само виводи відповідно до пунктів 2.5 «Ходу виконання роботи».

5. ЛІТЕРАТУРА

6. Харкевіч а.А., Спектр і аналіз. Стор. 13.19, 42.46.

7. Марпл - мл. С.Л., Цифровий спектральний аналіз і його застосування. Стор. 164.184.

8. КОНТРОЛЬНІ ВОПОСИ

9. До якого класу сигналів має бути віднесений досліджуваний в даній роботі сигнал на етапі завдання, різних етапах обробки, на етапі видачі результатів обробки?

10. Як можна оцінити абсолютне значення амплітуди спектральною компоненти сигналу по її спектру амплітуд, визначеною в логарифмічному масштабі?

11. Як впливає збільшення об'єму вибірки на точність оцінки частоти гармонійною компоненти складного сигналу?

12. Як впливає використання вікон, що «зважують», на точність частотних оцінок? Відповідь сформулювати як для «сильних», так і для «слабких» компонент, таких, що входять до складу сигналу.

13. У яких випадках доцільно використовувати логарифмічний, а в яких лінійний масштаб при оцінюванні складного, полігармонічного сигналу?

 

 

ЛАБОРАТОРНА РОБОТА №2