Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единица измерения количества информации.Содержание книги Поиск на нашем сайте
Для количественного определения любой величины необходимо определить единицу измерения. Для определения количества информации необходимо также ввести единицу измерения. За единицу количества информации принято такое количество информации, которое содержит сообщение уменьшающее степень неопределенность в два раза. Такая единица названа бит. Сообщение, уменьшающее степень неопределенности в два раз, несет 1 бит информации. Сообщение об одном событии из двух равновероятных несет 1 бит информации. Формула Хартли. Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации, заключенное в этом сообщении, – i бит и число N – количество событий связаны формулой: 2i = N. Данная формула является показательным уравнением относительно неизвестной i. Из математики известно, что решение такого уравнения имеет вид:
Если N равно целой степени двойки (2,4,8 и т.д.), то такое уравнение можно решить в уме. В противном случае, количество информации становится нецелой величиной, и для решения задачи придется воспользоваться таблицей логарифмов. Формула (1) является частным случаем формулы Р. Хартли, которая в общем случае имеет вид:
Здесь Н – количество информации, k – коэффициент пропорциональности, m – число возможных выборов, a – основание логарифма. Чаще всего принимают k = 1 и a = 2. Примеры. 1. При бросании монеты сообщение о результатах (выпал «орел») несет 1 бит информации. Оба варианта равновероятны. 2 i =2 следовательно i = 1 бит. 2. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере? Дано: N = 32 (количество событий) Решение: по формуле
Ответ: сообщение несет 5 бит информации. 3. Каково было количество возможных событий, если после реализации одного из них мы получили количество информации равное 3 бит? 7 бит? а) Дано: i = 3 (количество информации) Решение: Ответ: было 8 возможных событий. б) Дано: i = 7 (количество информации) Решение: Ответ: было 128 возможных событий.
Формула Шеннона. Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения «орла» и «решки» будут различаться. Рассмотрим еще один пример: в коробке имеется 50 шаров из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании «не глядя» попадется белый шар больше, чем вероятность попадания черного. Сделанное нами качественное заключение о вероятностях событий в рассмотренном примере – интуитивно понятно. Однако вероятность может быть выражена количественно. В нашем примере: обозначим рч – вероятность попадания при вытаскивании черного шара, рб - вероятность попадания при вытаскивании белого шара; тогда: рч = 10/50 = 0.2, рб = 40/50 = 0.8; отсюда – вероятность попадания белого шара в 4 раза больше, чем черного. Из рассмотренного примера можно сделать вывод: если N – это общее число возможных исходов какого-то процесса (вытаскивания шара, получения оценки и т.д.), и из них интересующее нас событие (вытаскивание белого шара, получение пятерки) может произойти K раз, этого события равна K/N. Вероятность выражается в долях единицы. В частном случае, вероятность достоверного события равна 1 (из 50 белых шаров вытащен белый); вероятность невозможного события равна нулю (из 50 белых шаров вытащен черный шар). Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии. Формулу для вычисления количества информации для событий с различными вероятностями предложил К. Шеннон в 1948 году. В этом случае количественная зависимость между вероятностью события (р) и количеством информации в сообщении о нем выражается формулой:
В нашем примере: количество информации в сообщении о попадании белого шара и черного шара:
Удобнее в качестве меры количества информации пользоваться не значением i, а средним значением количества информации, приходящейся на реализацию одного из возможных событий:
где I — количество информации, N — количество возможных событий, pi — вероятности отдельных событий. В нашем примере: количество информации, которое мы получим в сообщении о попадании белого шара или черного шара (после реализации одного из возможных событий):
Для частного, но широко распространенного и рассмотренного выше случая, когда события равновероятны (рi = I/N), величину количества информации I можно рассчитать по формуле:
В рассмотренном выше примере, изменив условия следующем образом: в коробке лежат 50 пронумерованных шаров одинакового цвета; количество информации, которое мы получим при сообщении “достали шар с номером 25” определим по формуле I = Iog250 = 5,64386 бит. Таким образом, когда события равновероятны, мы получим большее количество информации (5,64386 бит), чем когда события неравновероятны (2,282892 бит). Количество информации, которое мы получаем, достигает максимального значения, если события равновероятны. Примеры: 1. В корзине лежат 32 клубка шерсти. Среди них – 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти? Дано: N=32, K=4 Решение: 1. Найдем вероятность события – попал красный клубок шерсти: рк=4/32=1/8 2. По формуле (2) определим количество информации, которое несет сообщение «достали красный клубок шерсти» Ответ: сообщение «достали красный клубок шерсти» несет 3 бита информации. 2. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в корзине? Дано: N=64, i =4 Решение: 1. Найдем вероятность события – попал белый карандаш: рб=К/64 2. По формуле (2) составим следующее выражение 3. По определению логарифма: 24=64/К -> 16K=64 -> K=4 Ответ: в коробке с цветными карандашами 4 белых карандаша.
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.107 (0.008 с.) |

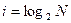 (логарифм от N по основанию 2). (1)
(логарифм от N по основанию 2). (1)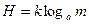
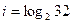 , по определению логарифма получаем i = 5
, по определению логарифма получаем i = 5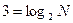 , по определению логарифма (23 = 8) получаем N = 8
, по определению логарифма (23 = 8) получаем N = 8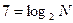 , по определению логарифма (27 = 128) получаем N =128
, по определению логарифма (27 = 128) получаем N =128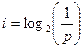 (2).
(2).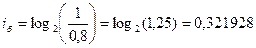 бит;
бит;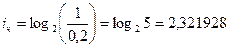 бит.
бит.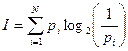 (3).
(3).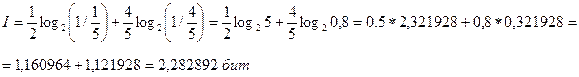
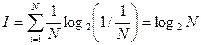 (4).
(4).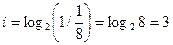 бит.
бит.