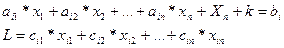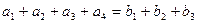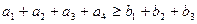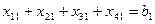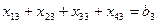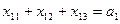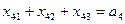Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні теоретичні положення.Содержание книги Поиск на нашем сайте
12.2.1 Ставлення задачи лінійного програмування.
Прикладом задачи лінійного програмування може служити транспортна задача. У пунктах А1,…,Аn знаходяться склади, де храняться товари у кількості Х1,…,Хn. У пунктах В1,…,Вm знаходяться споживачі, яким треба поставити ці товари у кількості Y1,…,Ym відповідно. Будемо роздивляти випадок, коли на складі Ai знаходиться товар Xi. Дij - вартість перевезення одиниці вантажа між пунктами Аi та Вj. Дослідим операцію перевезення товару споживачам у кількостях для того, щоб задовольнити потреби споживачів. Позначимо через хij кількість товару, перевозимого з Аi у Вj. Щоб задовольнити необхідні запити треба, щоб хij задовольняло нерівності
Але зі складу номер i ми не можемо вивезти продукта більш, ніж там є. Це означає, що шукані величини повинні задовольняти ще одній системі нерівностей
Задовольнити умовам (1) та (2) та виконати план перевезеннь, забезпечуючий запити, можна чісленою кількістю способів. Для того, щоб дослідник операцій зміг вибрати визначене рішення, повинно бути сформульоване деяке правило відбору, визначаєме за допомогою критерія, який відображає наше суб’єктивне представлення цілі. При цьому ми отримаємо одну з можливих оцінок обраного рішення. Проблема критерію вирішується незалежно від досліджуваної операції, тобто критерій повинен бути задан оперуючою стороною. Уданій задачі одним з критеріїв буде вартість перевезень, яка визначається:
Задачу о перевезеннях можна слідуючим чином: визначити хij, задовольняюче обмеженням (1) та (2) та забезпечуюче мінімальне значення функції (3). Обмеження (2) – умова балансу або закон зберігання, тобто умова фізичного типу. Умова (1) називається метою операції. Ці дві умови складають модель операції, Реалізація операції буде залежати від критеріїв. Тобто необхідними посиланнями задачи лінійного програмування є система рівняннь, які називаються обмеженнями, та цільова функція, відображаюча крітерій дослідження.
12.2.2 Опис алгоритму вирішення задач лінійного програмування.
Оскільки у задачах лінійного програмування число змінних більш числа рівнянь (n>m), то маємо нескінчену множину рішень. Іншими словами, маємо множину наборів змінних, х1,х2,х3,…, xn, які в принципі задовольняють усім заданим умовам та кожний такий набір можна вважати рішенням. Так як усі xi є які то фізичні
величини, вони не можуть бути <0, отже існують додаткові обмеження: хi>=0…хn>=0. Частіше за усе у задачах лінійного програмування усі або декілька обмежень мають вид нерівностей, але такі нерівності, легко перетворити у рівняння, вводячи додаткову змінну: Xn+k. Тобто у загальному вигляді система рівнянь буде мати такий вигляд:
Наприклад: Нехай маємо 4 склади А1,А2,А3,А4. На цих складах маємо продукцію а1,а2,а3. Маємо 3 споживача В1, В2, В3 яким відповідно треба завезти продукцію у кількості в1, в2, в3. Якщо на цих складах була б кількість продукції, для задоволення запитів, то виконалася б рівняння:
Але частіше всього нерівність
Позначимо через Cij кошт перевезення одиниці вантажу з одного пункта у інший. Обмеження та цільова функція виглядають так:
х – кількість вантажу, яке перевозиться з кожного складу, кожному споживачів.
Головною ціллю задач лінійного програмування є знаходження оптимальних значень х, себто з множини значень треба вибрати одне, те саме, що обертає у мінімум лінійну форму цільової
функції. Оскільки число змінних більше, ніж число рівнянь, для отримання однозначного рішення необхідно зменшити число змінних. Для цього уявимо х =0. Залишившуся систему можна вирішити звичайними методами. Набір використаних для рішення m змінних зветься базисом. Інші n-m змінні звуться незалежними. У кожній реальній системі може існувати декілька базисів, кожний зі своїм набором базисних та незалежних змінних. Якщо серед базисних рішень будуть такі які надають від’ємні значення змінним, то вони є неприпустимими і виключаються. Серед припустимих базисних рішень шукаються такі, які мінімізують (максимізують) лінійну цільову функцію. Ці рішення і є оптимальними.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.007 с.) |

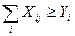 (1)
(1)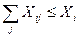 (2)
(2)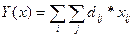 (3)
(3)