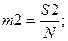Головні теоретичні положення.

 

10.2.1 Постановка задачи знаходження параметрів розподілу.

 

Для оцінки центру групування вибірки випадкових величин використовується:

середнє арифметичне;

медіана;

мода.

 

Середнє арифметичне для вибірки випадкових величин Х1, Х2,..., ХN розраховується за формулою:

 

 

Медіана дорівнює середньому члену вибірки випадкових чисел Х1, Х2,..., ХN поставлених у зростаючому порядку, при непарном N. Якщо N – парне, медіана дорівнює півсумі двох середніх членів. Модой зветься таке значення випадкової величини, ймовірість отримання якого найбільша.

Розсіювання випадкових величин у виборці характеризується:

емпіричною дисперсією;

розмахом.

Емпірична дисперсія S# для вибірки випадкових величин Х1, Х2,...

ХN розраховується за формулою:

Розмах розраховується як різниця максимального та мінімального члена вибірки.

Розподілення випадкової величини зветься розміщена за зростанням сукупність значеннь випадкових величин із вказівкою ймовірності їх виникання.

Емпіричне розподілення може бути представлено у вигляді гістограми, тобто ступенчатого графіку, ординати якого співпадають з частістю влучання даної випадкової величини у інтервал значеннь, відложений по вісі абсцис.

При построєнні гістограм частість Fi й кількість інтервалів розраховується за формулою:

де: Ni – кількість влученнь значення випадкової величини до і-го інтервалу;

N – об’єм вибірки.

Емпіричне розподілення випадкової величини Х може бути описано аналітично за допомогою функції плотності ймовірності f(X) теоретичного розподілення.

10.2.2 Опис методіки перевірки гіпотези про закон розподілення.

 

Нехай надана вибірка незалежних випадкових чисел Х1, Х2,..., ХN маючих емпіричне розподілення Fn(X). Для перевірки узгодження емпіричного розподілення Fn(X) з теоретичним розподіленням F(X) використовується У – критерій Колмогорова та nw – критерій Мізеса – Смірнова. Попередня оцінка виду розподілення може бути зроблена порівнянням гистограм емпіричного та теоретичного розподіленнь.

Перевірка за допомогою критерія Колмогорова виконується наступним чином. Вибіркова послідовність {Xi} впорядковується у незменшующуюся послідовність {Xk}. Розраховується абсолютне значення максимального розходження Dnміж емпіричним та теоретичним розподіленням:

 

З отриманого значення Dn розраховується величина

яка порівнюється з критичним значенням.

 

IV. Опис методіки.

 

Необхідно розробити алгоритми та програми:

 

Програма RSP.

Алгоритм програми це організація друку масива з результатами спостереженнь по вказаним видам масива й назві файлу.

 

Програма PZR.

 

Алгоритм програми складається із слідуючих дій:

Вводиться код розподілення IFCOD, об’єм вибірки N, кількість інтервалів M, параметри розподілення a,b,c, верхня межа АНІ, й нижня межа ALO для побудови гістограми;

Результати спостереженнь А1, і=1,N, вводяться з файлу, де записан масив Аі, і=1,N.

Розраховуються:

суми

моменти

центральні моменти

середне

дисперсія

асиметрія

Розраховується крок STEP, верхні ВНІ(К) та нижні BLO(К) границі інтервалов

 

STEP = (AHI-ALO) / M;

BLO(K) = ALO + STEP * (K-1);

BHI(K) = ALO + STEP * K;

K=1, M;

Визначається кількість та накопичена кількість, процент й накопичений процент спостереженнь, влучивших в інтервал [BLO(K), BHI(K)], при К = 1, М для чого розробити програму FRQ.

Оцінюється узгодження емпіричного та теоретичного розподіленнь за крітеріями Колмогорова та Мізес – Смірнова, для чого розробляється підпрограма (процедура).

 

Програма TUTEST.

 

Алгоритм складається із слідуючих дій:

Вводяться результати спостереженнь з двох, в кожном з яких знаходяться двохмірні масиви з елементами

A(I,J), I = 1, NA; B(I,J), I = 1, NB; J = 1, NJ, де NA, NB – об’єми порівнюємих вибірок, NJ – число порівнюємих вибірок.

Розраховуються квантіли розподіленнь Фішера, Ст’юдента, Гауса виходячи з даної довірчої ймовірностіза допомогою п/програм QNTF, QNT.

Розраховуютьсясередні та дисперсії вибірок типа А та В для кожної пари вибірок.

Розраховується T – критерій за п/програмою TTEST та U – критерій за п/програмою UTEST.

Порівнянням розрахованих значеннь статистичних критеріїв з їх табличними значеннями формується заключення о різниці вибірок для кожної пари.