
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эвристика объединения по рангуСодержание книги Поиск на нашем сайте
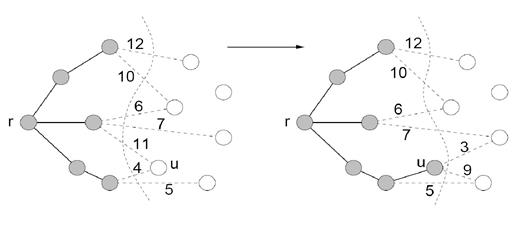
Рассмотрим здесь другую эвристику, которая сама по себе способна ускорить время работы алгоритма, а в сочетании с эвристикой сжатия путей и вовсе способна достигнуть практически константного времени работы на один запрос в среднем. Эта эвристика заключается в небольшом изменении работы: если в начальной реализации то, какое дерево будет присоединено к какому, определяется случайно, то теперь будем это делать на основе рангов. Есть два варианта ранговой эвристики: в одном варианте рангом дерева называется количество вершин в нём, в другом — глубина дерева (точнее, верхняя граница на глубину дерева, поскольку при совместном применении эвристики сжатия путей реальная глубина дерева может уменьшаться). В обоих вариантах суть эвристики одна и та же: при выполнении будем присоединять дерево с меньшим рангом к дереву с большим рангом. Асимптотика работы системы непересекающихся множеств при использовании только ранговой эвристики, без эвристики сжатия путей, будет логарифмической на один запрос в среднем: O(log n). При совместном применении эвристик сжатия пути и объединения по рангу время работы на один запрос получается O(α(n)) в среднем, где α(n) — обратная функция Аккермана, которая растёт очень медленно, настолько медленно, что для всех разумных ограничений она не превосходит 4 (примерно для n<=10600). Именно поэтому про асимптотику работы системы непересекающихся множеств уместно говорить "почти константное время работы". Асимптотическая оценка алгоритм Крускала Инициализация – O(V) Упорядочение ребер - O(E logE) Операции сравнения выполняются O(E) раз за время O(E α(V)). Общее время работы - O(E logE)
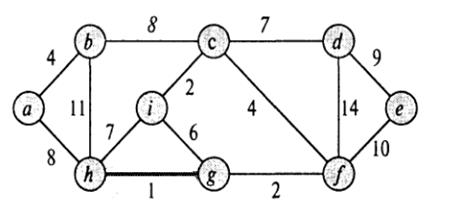
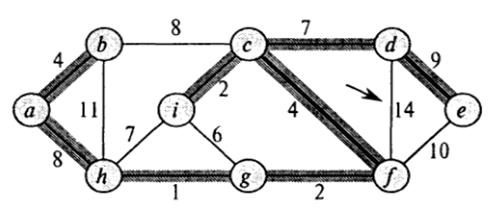
Построение минимального покрывающего дерева, алгоритм Прима Искомый минимальный остов строится постепенно, добавлением в него рёбер по одному. Изначально остов полагается состоящим из единственной вершины (её можно выбрать произвольно). Затем выбирается ребро минимального веса, исходящее из этой вершины, и добавляется в минимальный остов. После этого остов содержит уже две вершины, и теперь ищется и добавляется ребро минимального веса, имеющее один конец в одной из двух выбранных вершин, а другой — наоборот, во всех остальных, кроме этих двух. И так далее, т.е. всякий раз ищется минимальное по весу ребро, один конец которого — уже взятая в остов вершина, а другой конец — ещё не взятая, и это ребро добавляется в остов (если таких рёбер несколько, можно взять любое). Этот процесс повторяется до тех пор, пока остов не станет содержать все вершины (или, что то же самое, n-1 ребро).
В итоге будет построен остов, являющийся минимальным. Если граф был изначально не связен, то остов найден не будет (количество выбранных рёбер останется меньше n-1).
Prim(Gfw,г) { for each (u in V) { // initialization key[u] = +infinity; color [u] = white; } key[r] =0; // start at root pred [r] = nil; Q = new PriQueue(V); // put vertices in Q while (Q.nonEmpty()) { // until all vertices in MST u = Q.extractMin(); // vertex with lightest edge for each (v in Adj[u]) { if ((color [v] == white) && (w(u,v) < key [v])) { key[v] = w(u,v); // new lighter edge out of v Q.decreaseKey(v, key [v]); pred [v] = u; } } color[u] = black; }
}
Анализ Инициализация – O(V) Цикл выполняется V раз и каждая операция extractMin выполняется за - O(logV) раз, всего O(V logV) раз Цикл for выполняется O(E) раз, decreaseKey - за время O(logV). Общее время работы - O(V log V +E logV)= O(E logV)
Происк кратчайшего пути. Алгоритм Дейкстры Задача поиска кратчайшего пути
Вес пути p = (v0, v1..... vk) равен суммарному весу входящих k в него ребер,
соотношением: Кратчайший путь из вершины u в вершину v – это любой путь p, что w(p) = d(u, v) Задача поиска кратчайшего пути • из заданной вершины во все остальные • между всеми парами вершин Свойство кратчайшего пути Пусть p = (v1, v2..... vk) - кратчайший путь из вершины v1 к вершине vk в заданном взвешенном ориентированном графе G = (У. Е) с весовой функцией w: Е → R a pij = (vi, vi+1.....vj) - частичный путь пути p, который проходит из вершины vi к вершине vj для произвольных i и j (1 ≤ i < j ≤ k). Тогдa pij – кратчайший путь из вершины vi к vi Dijkstra(G, w, s) { for each (u in V) { // initialization d [u] = +infinity color [u] = white pred[u] = null } d[s] =0 // dist to source is 0 Q = new PriQueue(V) // put all vertices in Q while (Q.nonEmpty()) { // until all vertices processed u = Q.extractMin(} // select u closest to s for each (v in Adj[u]) { if (d[u] + w(u,v) < d[v]) { // Relax(u,v) d [v] = d [u] + w(u,v) Q.decreaseKey(v, d[v]) pred [v] = u } } color [u] = black } [The pred pointers define an '1 inverted'' shortest path tree] }
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.196.68 (0.01 с.) |




 Дан граф G = (V. Е) с весовой функцией w: Е → R.
Дан граф G = (V. Е) с весовой функцией w: Е → R.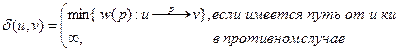 Вес кратчайшего пути из вершины u в вершину v определяется
Вес кратчайшего пути из вершины u в вершину v определяется



