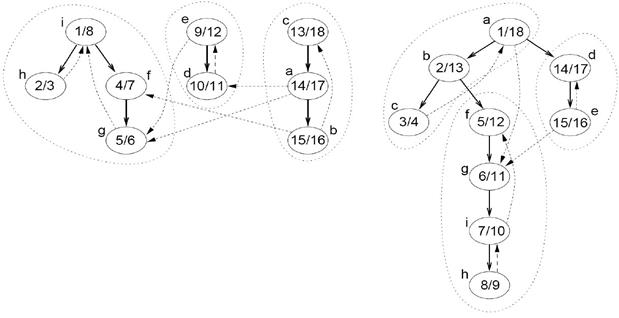
Сильно связные компоненты, алгоритм поиска

Сильно связанной компонентой ориентированного графа G называется максимальное множество вершин U с таким свойством: любые две вершины u и v из U достижимы друг из друга.

FindStrongComp(G)

1 DFS (G) ► вычисли м f[u] для каждой вершины и

2 R ← Reverse(G) ► инвертируем все ребра в G

3 SortByF(R) ► сортируем вершины в R по f[u] по убыванию

4 DFS(R)

Результат: каждое DFS-дерево в R является сильно

связанным компонентом.

Каждое ребро в G^T, соединяющее два сильно связных компонента, идет от компонента с более ранним временем завершения (при поиске в глубину) к компоненту с более поздним временем завершения.

Сильно связные компоненты и DFS

Алгоритм поиска сильно связных компонентов

Построение минимально покрывающего дерева, алгоритм Крускала

Алгоритм Крускала изначально помещает каждую вершину в своё дерево, а затем постепенно объединяет эти деревья, объединяя на каждой итерации два некоторых дерева некоторым ребром.

Перед началом выполнения алгоритма, все рёбра сортируются по весу (в порядке неубывания). Затем начинается процесс объединения: перебираются все рёбра от первого до последнего (в порядке сортировки), и если у текущего ребра его концы принадлежат разным поддеревьям, то эти поддеревья объединяются, а ребро добавляется к ответу.

По окончании перебора всех рёбер все вершины окажутся принадлежащими одному поддереву, ответ найден.

Kruskal (G = (V, Е), w) {

А = {} // initially A is empty

for each (u in V) Create_Set(u) // create set for each vertex

Sort E in increasing order by weight w

for each ((u, v) from the sorted list) {

if (Find_Set(u)!= Find_Set(v)) { // u and v in different trees

Add (u, v) to A

Union (u, v)

}

}

return A

}

Процедуры

Create — Set (u) - создать множество из одной вершины u.

Find — Set (u) - найти множество, которому принадлежит вершина u возвращает, в каком множестве находится указанный элемент. На самом деле при этом возвращается один из элементов множества (называемый представителем или лидером). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов Union).

Если вызов Find — Set для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах.

Union (u,v) - объединить множества, которые содержат вершины u и v

Множества элементов будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества.

При реализации это означает, что мы заводим массив parent, в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте).

Чтобы создать новый элемент (операция Create — Set), мы просто создаём дерево с корнем в вершине v, отмечая, что её предок — это она сама.

Чтобы объединить два множества (операция Union(a,b)), мы сначала найдём лидеров множества, в котором находится a, и множества, в котором находится b. Если лидеры совпали, то ничего не делаем — это значит, что множества и так уже были объединены. В противном случае можно просто указать, что предок вершины b равен f (или наоборот) — тем самым присоединив одно дерево к другому.

Наконец, реализация операции поиска лидера (Find — Set(v)) проста: мы поднимаемся по предкам от вершины v, пока не дойдём до корня, т.е. пока ссылка на предка не ведёт в себя. Эту операцию удобнее реализовать рекурсивно.

Эвристика сжатия пути

Эта эвристика предназначена для ускорения работы Find — Set().

Она заключается в том, что когда после вызова Find — Set(v) мы найдём искомого лидера p множества, то запомним, что у вершины v и всех пройденных по пути вершин — именно этот лидер p. Проще всего это сделать, перенаправив их parent на эту вершину p.

Таким образом, у массива предков parent смысл несколько меняется: теперь это сжатый массив предков, т.е. для каждой вершины там может храниться не непосредственный предок, а предок предка, предок предка предка, и т.д.

С другой стороны, понятно, что нельзя сделать, чтобы эти указатели parent всегда указывали на лидера: иначе при выполнении операции Union пришлось бы обновлять лидеров у O(n) элементов.

Таким образом, к массиву parent следует подходить именно как к массиву предков, возможно, частично сжатому.

Применение эвристики сжатия пути позволяет достичь логарифмическую асимптотику: на один запрос в среднем