Жадные алгоритмы, основные особенности

• Жадные алгоритмы - производится локально оптимальный выбор в надежде, что он приведет к оптимальному решению всей задачи.

• Динамическое программирование – разбить задачу на подзадачи и не вычислять подзадачи более одного раза (использовать память).

Жадный алгоритм — алгоритм, заключается в принятии оптимальных решений на каждом шаге, где общее решение задачи складывается из оптимальных решений на предыдущих шагах.

Для задач, решаемых жадными алгоритмами, характерны две особенности:

• к ним применим Принцип жадного выбора,

• они обладают свойством Оптимальности для подзадач.

Принцип жадного выбора

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение.

В типичном случае доказательство оптимальности следует такой схеме:

• Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого.

• Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной.

• Рассуждение завершается по индукции.

Оптимальность для подзадач

Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач.

 

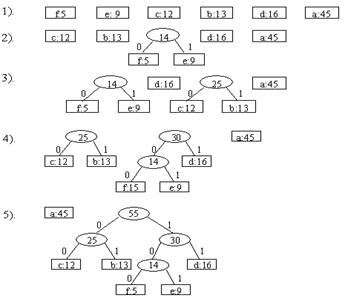
Построение кода Хаффмена

Любое сообщение состоит из последовательности символов некоторого алфавита. Зачастую для экономии памяти, для увеличения скорости передачи информации возникает задача сжатия информации. В этом случае используются специальные методы кодирования символов. К таким относятся коды Хаффмена, которые дают сжатие от 20% до 90% в зависимости от типа информации.

Алгоритм Хаффмена находит оптимальные коды символов исходя из частоты использования символов в сжимаемом тексте.

Алгоритм Хаффмена является примером жадного алгоритма.

Пусть в файле длины 100000 символы известны частоты символов:

Символ	Кол-во	Код№1	Код №2
a
b
c
d
e
f

Нужно построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом. При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ тратится минимум три бита и на весь файл уйдет 300000 битов.

Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся символы – длинными. При кодировке на весь файл уйдет (45*1 + 13*3 + 12*3 + 16*3 + 9*4 + 5*4)*1000 = 224000. То есть, неравномерный код дает около 25% экономии.

Префиксные коды

Рассмотрим коды, в которых для каждой из двух последовательностей битов, представляющих различные символы, ни одна не является префиксом другой. Такие коды называются префиксными кодами.

При кодировании каждый символ заменяется на свой код. Например, строка abc выглядит как 0101100. Для префиксного кода декодирование однозначно и выполняется слева направо.

Первый символ текста, закодированного префиксным кодом, определяется однозначно, так как его кодовое слово не может быть началом какого-либо другого символа. Определив этот символ и отбросив его кодовое слово, повторяем процесс для оставшихся битов и так далее.

Например, строка 001011101 разбивается на части 0.0.101.1101 и декодируется как aabe.

Для эффективной реализации декодирования нужно хранить информацию о коде в удобной форме. Одна из возможностей – представить код в виде кодового двоичного дерева, листья которого соответствуют кодируемым символам. При этом путь от корня до кодируемого символа определяет кодирующую последовательность битов: переход по дереву налево дает 0, а переход направо – 1.

Во внутренних узлах указана сумма частот для листьев соответствующего поддерева.

Оптимальному для данного файла коду всегда соответствует двоичное дерево, в котором всякая вершина, не являющаяся листом, имеет двух сыновей. Равномерный код не является оптимальным, так как в соответствующем ему дереве есть вершина с одним сыном.

Дерево оптимального префиксного кода для файла, в котором используются все символы из некоторого множества С и только они содержат ровно | С | листьев по одному на каждый символ и ровно | С | - 1 узлов, не являющихся листьями.

Зная дерево Т, соответствующее префиксному коду, легко найти количество битов, необходимое для кодирования файла. Для каждого символа с из алфавита С, пусть f [c] означает число его вхождений в файл, а dT (c) – глубину соответствующего ему листа и, следовательно, длину последовательности битов, кодирующей с. Тогда для кодирования файла потребуется:

битов

Эта величина называется стоимостью дерева Т. Необходимо минимизировать эту величину.

Хаффмен предложил жадный алгоритм, который строит оптимальный префиксный код. Алгоритм строит дерево Т, соответствующее оптимальному коду снизу вверх, начиная с множества из | С | листьев и делая | С | - 1 слияний.

Для каждого символа задана его частота f [c]. Для нахождения двух объектов для слияния используется очередь с приоритетами Q, использующая частоты f в качестве приоритетов – сливаются два объекта с наименьшими частотами.

В результате слияния получается новый объект (внутренняя вершина), частота которого считается равной сумме частот двух сливаемых объектов. Эта вершина заносится в очередь.

Huffman (C)

1. n ←│C│ │ C │- мощность С

2. Q ← C Q – очередь с приоритетами

3. for i ← 1 to n-1

4. do z ← Create_Node () z – узел, состоящий из полей f, left, right

5. x ← left [z] ← Dequeue (Q)

6. y ← right [z] ← Dequeue (Q)

7. f[z] ← f[x] + f[y]

8. Enqueue (Q, z)

9. return Dequeue (Q) вернуть корень дерева

 

 

Оценка

Очередь реализована в виде двоичной кучи.

Создать очередь можно за O(n).

Алгоритм состоит из цикла, который выполняется n-1 раз.

Каждая операция с очередью выполняется за O(log n).

Общее время работы O(n log n).