Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Асимптотическая оценка алгоритмаСодержание книги Поиск на нашем сайте
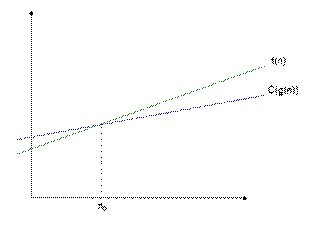
Асимптотическая оценка алгоритма • Анализ алгоритмов – теоретическое исследование производительности компьютерных программ и потребляемых ими ресурсов. • Быстродействие – время работы алгоритма, в зависимости от объема входных данных. • Определяется функцией Т(n), где n – объем входных данных Виды анализа • Наихудший случай: T(n) – максимальное время для любых входных данный размера n. • Средний случай: T(n) – ожидаемое время для любых входных данных размера n. • Наилучший случай – минимальное время работы. Асимптотическая оценка O - нотация: асимптотическая верхняя граница f (n) = O(g(n)) Þ ($c > 0, n0> 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n0) O(g(n)) = {f (n): $ c > 0, n0 > 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n0} Пример: 2n2 = O(n3)
Ω - нотация: асимптотическая нижняя граница Ω(g(n)) = {f (n): $c > 0, n0 > 0 Þ 0 ≤ c · g(n) ≤ f (n), n ≥ n0}
Пример 1 f(n)=1/2n2-3n Докажем, что g(n)=n2 является асимптотической оценкой f(n)
При С2= 1/2 неравенство будет выполнятся (n→∞) n0=7, так как n=6 брать нельзя (С1и С2>0) C1= 1/14, С2= 1/2 из выражения – 1/2-3/7=1/14. Утверждение верно Пример 2 f(n)=6n3
Асимптотические оценки: θ(1), θ(log2n), θ(n), θ(n*log2n), θ(n2), θ(n3), θ(2n)
Методика оценки не рекурсивных алгоритмов. Пример
Рекурсивные алгоритмы, построение асимптотической оценки. Пример Сортировка слиянием sort(А,p,r) //p - начало массива, r – конец массива T(n) { if(p < r) //1 { q=(p + r)/2; //Вычисляем середину массива 1 sort(А,p,q); //сортируем левую часть T(n/2) sort(А,q+1,r); //сортируем правую часть T(n/2) merge(p,q,r); //сливаем два массива в один n } }
Дерево рекурсии: T(n) = 2*T(n/2) +cn, с –const, c>0 Методика оценки рекурсивных алгоритмов. Метод итераций На основании формулы T(n) записываем формулу для меньшего элемента, находящегося в правой части формулы для T(n). Подставляем правую часть полученной формулы в исходную формулу Выполняем первые два шага, пока не развернем формулу в ряд без функции T(n) Оценим полученный ряд на основании арифметической или геометрической прогрессии Пример: T(n)=T(n-1)+n, T(1)=1 T(n)=θ(g(n)), g(n)=? T(n-1)=T(n-2)+(n-1) T(n-2)=T(n-3)+(n-2) T(n)= T(n-1)+n= T(n-2)+(n-1)+n= T(n-3)+(n-2)+(n-1)+n=… 1+…(n-2)+(n-1)+n= n*(n+1) T(n)=θ(n2) Дерево рекурсии - графический метод отображения подстановки соотношения самого в себя T(n)=2T(n/2)+n2 n2 T(n/2) T(n/2)
n2 (n/2)2 (n/2)2 T(n/4) T(n/4) T(n/4) T(n/4)
T(n)=θ(n2) Mетод подстановки
Догадка: T(n) = (n log n)
Посылка индукции: T(n) ≤ с * n* log n, c>0 Пусть эта оценка верна для n/2 T(n/2) ≤ c*(n/2)*log(n/2) Подставим ее в исходную формулу для T(n) T(n) ≤ 2*(c*(n/2)*log(n/2))+n ≤ c*n*log(n/2)+n = c*n*log n - c*n*log 2 +n = c*n*log n - c*n +n ≤ c*n*log n c≥1, n ≥ 2 Основная теорема о рекуррентных оценках T (n) = aT (n/b) + f (n), a ≥ 1, b > 1, f (n) − (f (n) > 0, n > n0) Алгоритмы сортировки массивов за полиномиальное время Сортировка - процесс перестановки объектов заданной совокупности в определенном порядке (возрастающем или убывающем). Целью сортировки обычно является облегчение последующего поиска элементов в отсортированном множестве. Сортировка простыми вставками void sort_by_insertion(key a[], int N) { key x; int i, j; for (i=1; i < N; i++) { x = a[i]; for (j=i-1; (j>=0)&& (x < a[j]); j--) a[j + 1] = a[j]; a[j + 1] = x; } } Анализ сортировки простыми вставками Наихудший случай: упорядоченный в обратном порядке массив Количество сравнений: С (N) = 1 + 2 + 3 +... + N - 1 = (N *(N -1))/2= О (N2) Общее время: T(N) = θ(N2) Сортировка простым обменом. Метод пузырька. void bubble_sort (key а[], int N) { int i, j; key x; for (i=0; i<N-l; i++) for (j=N-l; j>i; j--) if (a[j-l] > a[j]) { x = a [ j ]; a [ j ] = a [ j -1]; a [ j -1] = x; } } Анализ сортировки простым обменом Наихудший случай: упорядоченный в обратном порядке массив Количество сравнений: C(N) = (N - 1) + (N - 2) +... + 1 = (N * (N-1))/2 = O(N2) Общее время: T(N) = θ(N2) Добавление class BTree{ Node* root; Node* _Add(Node *r, T s) { if(r == 0) r = new Node(s); else if(s < r->inf) r->left = _Add(r->left, s); else r->right = _Add(r->right, s); return r; } Удаление элемента из дерева Дерево Т с корнем n и ключом K. удалить из дерева Т узел с ключом K (если такой есть). Алгоритм: Если дерево T пусто, остановиться; Иначе сравнить K с ключом X корневого узла n. Если K>X, рекурсивно удалить K из правого поддерева Т; Если K<X, рекурсивно удалить K из левого поддерева Т; Если K=X, то необходимо рассмотреть три случая. Если обоих детей нет, то удаляем текущий узел и обнуляем ссылку на него у родительского узла; Если одного из детей нет, то значения полей ребёнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом m; Если оба ребёнка присутствуют, то найдём узел m, являющийся следующим за данным; скопируем данные (кроме ссылок на дочерние элементы) из m в n; рекурсивно удалим узел m. Элемент следующий за данным Дано: дерево Т и ключ х Возвращаем указатель на следующий за х элемент или NULL, если элемент х последний в дереве. Алгоритм: Отдельно рассматривает два случая. Если правое поддерево вершины х не пусто, то следующий за х элемент – минимальный элемент в этом поддереве. Иначе, если правое поддерево вершины х пусто. Переходим от х вверх, пока не найдём вершину, являющуюся левым сыном своего родителя. Этот родитель (если он есть) и будет искомым элементом. Вставка узлов Вставка нового ключа в АВЛ-дерево выполняется так же, как это делается в простых деревьях поиска: спускаемся вниз по дереву, выбирая правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. Единственное отличие заключается в том, что при возвращении из рекурсии (т.е. после того, как ключ вставлен либо в правое, либо в левое поддерево) выполняется балансировка текущего узла. Возникающий при такой вставке дисбаланс в любом узле по пути движения не превышает двух, а значит применение вышеописанной функции балансировки является корректным. Удаление узлов Для удалении вершины из АВЛ – дерева за основу взят алгоритм, который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска. Находим узел p с заданным ключом k, в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min. При реализации возникает несколько вариантов. Прежде всего, если у найденный узел p не имеет правого поддерева, то по свойству АВЛ-дерева слева у этого узла может быть только один единственный дочерний узел (дерево высоты 1), либо узел p вообще лист. В обоих этих случаях надо просто удалить узел p и вернуть в качестве результата указатель на левый дочерний узел узла p. Пусть теперь правое поддерево у p есть. Находим минимальный ключ в этом поддереве. По свойству двоичного дерева поиска этот ключ находится в конце левой ветки, начиная от корня дерева. Применяем рекурсивную функцию findmin. функция removemin - удалением минимального элемента из заданного дерева. По свойству АВЛ-дерева у минимального элемента справа либо единственный узел, либо там пусто. В обоих случаях надо просто вернуть указатель на правый узел и по пути назад (при возвращении из рекурсии) выполнить балансировку. Хеш-таблицы, метод цепочек Прямая адресация применяется для небольших множеств ключей. Требуется задать динамическое множество, каждый элемент которого имеет ключ из множества U = {0,1,..., m - 1}, где m не слишком велико, никакие два элемента не имеют одинаковых ключей. Для представления динамического множества используется массив (таблицу с прямой адресацией), Т [0..m - 1], каждая позиция, или ячейка, которого соответствует ключу из пространства ключей U. Ячейка k указывает на элемент множества с ключом k. Если множество не содержит элемента с ключом k, то Т [k] = NULL.
Операция поиска по ключу занимает время O(1) Недостатки прямой адресации: • если пространство ключей U велико, хранение таблицы Т размером |U| непрактично, а то и вовсе невозможно — в зависимости от количества доступной памяти и размера пространства ключей • множество К реально сохраненных ключей может быть мало по сравнению с пространством ключей U, а в этом случае память, выделенная для таблицы Т, в основном расходуется напрасно. Хеш-функция – такая функция h, которая определяет местоположение элементов множества U в таблице T.
При хешировании элемент с ключом k хранится в ячейке h(k), хеш-функция h используется для вычисления ячейки для данного ключа k. Функция h отображает пространство ключей U на ячейки хеш-таблицы Т [О..m - 1]: h: U → {0,1,..., m -1}. величина h (к) называется хеш-значением ключа к. Когда множество К хранящихся в словаре ключей гораздо меньше пространства возможных ключей U, хеш-таблица требует существенно меньше места, чем таблица с прямой адресацией. Цель хеш-функции состоит в том, чтобы уменьшить рабочий диапазон индексов массива, и вместо |U| значений можно обойтись всего лишь m значениями. Требования к памяти могут быть снижены до θ(|К|), при этом время поиска элемента в хеш-таблице остается равным О(1) - это граница среднего времени поиска, в то время как в случае таблицы с прямой адресацией эта граница справедлива для наихудшего случая.
Коллизия – ситуация, когда два ключа отображаются в одну и ту же ячейку. Например, h(43) = h(89) = h(112) = k
Метод цепочек: Идея: Хранить элементы множества с одинаковым значением хэш-функции в виде списка.
Анализ Наихудший случай: если хэш-функция для всех элементов множество выдает одно и то же значение. Время доступа равно Θ(n), при |U | = n. Средний случай: для случая, когда значения хэш-функции равномерно распределены. Каждый ключ с равной вероятностью может попасть в любою ячейку таблицы, вне зависимости от того куда попали другие ключи. Пусть дана таблицы T[0..m - 1], и в ней хранится n ключей. Тогда, а = n/m - среднее количество ключей в ячейках таблицы. Время поиска отсутствующего элемента – Θ(1 + α). Константное время на вычисления значения хэш-функции плюс время на проход списка до конца, т.к. средняя длина списка - α, то результат равен Θ(1) + Θ(α) = Θ(1 + α) Если количество ячеек таблицы пропорционально количеству элементов, хранящихся в ней, то n = O(m) и, следовательно, α = n/m = O(m)/m = O(1), а значит поиск элемента в хэш-таблице в среднем требует времени Θ(1). Операции • вставка элемента в таблицу • удаление также требуют времени O(1) Выбор хэш-функции • Ключи должны равномерно распределятся по всем ячейкам таблицы. • Закономерность распределения ключей хэш-функции не должна коррелировать с закономерностями данных. (Например, данные – это четные числа). Методы: • Метод деления • Метод умножения
Метод деления h (k) = k mod m Проблема маленького делителя m Пример №1. m = 2 и все ключи четные Þ нечетные ячейки не заполнены. Пример №2. m = 2r Þ хэш не зависит от бито в выше r. Метод умножения Пусть m = 2r, ключи являются w-битными словами. h(k) = (A • k mod 2w) >> (w - r), где A mod 2 = 1 ∩ 2w-1 < A< 2w • He следует выбирать A близко к 2w-1 и 2w • Данный метод быстрее метода деления
Метод умножения: пример m = 8 = 23, w = 7
Открытая адресация: поиск • Поиск – также последовательное исследование • Успех, когда нашли значение • Неудача, когда нашли пустую клетку или прошли всю таблицу. Стратегии исследования • Линейная - h(k, i) = (h′(k) + i) mod m где h′(k) – обычная хэш-функция Данная стратегия легко реализуется, однако подвержена проблеме первичной кластеризации, связанной с созданием длинной последова- тельности занятых ячеек, что увеличивает среднее время поиска. • Квадратичная h(k, i) = (h′(k) + с1 i+ с2 i2) mod m где h′(k) – обычная хэш-функция • Двойное хеширование – h(k,i) = (h1(k) + i • h2(k)) mod m. Двойное хеширование Этот метод даёт отличные результаты, но h2(k) должен быть взаимно простым с m. Этого можно добиться: используя в качестве m степени двойки и сделав так, чтобы h2(k) выдавала только нечётные числа m = 2r иh2(k) – нечетная. • m - простое число, значения h2 – целые положительные числа, меньшие m Для простого m можно установить h1(k)=k mod m h2(k)=1+(k mod m’) m’ меньше m (m’ = m-1 или m-2) Открытая адресация: пример вставки Пусть дана таблица A: Двойное хеширование m=13 h1(k)=k mod 13 h2(k)=1+(k mod 11) k=14 Куда будет встроен элемент? Анализ открытой адресации Дополнительное допущение для равномерного хеширования: каждый ключ может равновероятно получить любую из m! перестановок последовательностей исследования таблицы независимо от других ключей. Поиск отсутствующего элемента
Открытой адресации а < 1 — const Þ O(1) Как же себя ведет а: • Таблица заполнена 50% Þ2 исследования • Таблица заполнена на 90% Þ 10 исследований • Таблица заполнена на 100% Þ m исследований
Принцип жадного выбора Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных выборов даёт глобально оптимальное решение. В типичном случае доказательство оптимальности следует такой схеме: • Доказывается, что жадный выбор на первом шаге не закрывает пути к оптимальному решению: для всякого решения есть другое, согласованное с жадным выбором и не хуже первого. • Показывается, что подзадача, возникающая после жадного выбора на первом шаге, аналогична исходной. • Рассуждение завершается по индукции. Оптимальность для подзадач Говорят, что задача обладает свойством оптимальности для подзадач, если оптимальное решение задачи содержит в себе оптимальные решения для всех её подзадач.
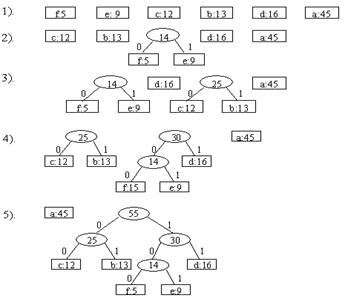
Построение кода Хаффмена Любое сообщение состоит из последовательности символов некоторого алфавита. Зачастую для экономии памяти, для увеличения скорости передачи информации возникает задача сжатия информации. В этом случае используются специальные методы кодирования символов. К таким относятся коды Хаффмена, которые дают сжатие от 20% до 90% в зависимости от типа информации. Алгоритм Хаффмена находит оптимальные коды символов исходя из частоты использования символов в сжимаемом тексте. Алгоритм Хаффмена является примером жадного алгоритма. Пусть в файле длины 100000 символы известны частоты символов:
Нужно построить двоичный код, в котором каждый символ представляется в виде конечной последовательности битов, называемой кодовым словом. При использовании равномерного кода, в котором все кодовые слова имеют одинаковую длину, на каждый символ тратится минимум три бита и на весь файл уйдет 300000 битов. Неравномерный код будет экономнее, если часто встречающиеся символы закодировать короткими последовательностями битов, а редко встречающиеся символы – длинными. При кодировке на весь файл уйдет (45*1 + 13*3 + 12*3 + 16*3 + 9*4 + 5*4)*1000 = 224000. То есть, неравномерный код дает около 25% экономии. Префиксные коды Рассмотрим коды, в которых для каждой из двух последовательностей битов, представляющих различные символы, ни одна не является префиксом другой. Такие коды называются префиксными кодами. При кодировании каждый символ заменяется на свой код. Например, строка abc выглядит как 0101100. Для префиксного кода декодирование однозначно и выполняется слева направо. Первый символ текста, закодированного префиксным кодом, определяется однозначно, так как его кодовое слово не может быть началом какого-либо другого символа. Определив этот символ и отбросив его кодовое слово, повторяем процесс для оставшихся битов и так далее. Например, строка 001011101 разбивается на части 0.0.101.1101 и декодируется как aabe. Для эффективной реализации декодирования нужно хранить информацию о коде в удобной форме. Одна из возможностей – представить код в виде кодового двоичного дерева, листья которого соответствуют кодируемым символам. При этом путь от корня до кодируемого символа определяет кодирующую последовательность битов: переход по дереву налево дает 0, а переход направо – 1. Во внутренних узлах указана сумма частот для листьев соответствующего поддерева.
Оптимальному для данного файла коду всегда соответствует двоичное дерево, в котором всякая вершина, не являющаяся листом, имеет двух сыновей. Равномерный код не является оптимальным, так как в соответствующем ему дереве есть вершина с одним сыном. Дерево оптимального префиксного кода для файла, в котором используются все символы из некоторого множества С и только они содержат ровно | С | листьев по одному на каждый символ и ровно | С | - 1 узлов, не являющихся листьями. Зная дерево Т, соответствующее префиксному коду, легко найти количество битов, необходимое для кодирования файла. Для каждого символа с из алфавита С, пусть f [c] означает число его вхождений в файл, а dT (c) – глубину соответствующего ему листа и, следовательно, длину последовательности битов, кодирующей с. Тогда для кодирования файла потребуется: битов Эта величина называется стоимостью дерева Т. Необходимо минимизировать эту величину. Хаффмен предложил жадный алгоритм, который строит оптимальный префиксный код. Алгоритм строит дерево Т, соответствующее оптимальному коду снизу вверх, начиная с множества из | С | листьев и делая | С | - 1 слияний. Для каждого символа задана его частота f [c]. Для нахождения двух объектов для слияния используется очередь с приоритетами Q, использующая частоты f в качестве приоритетов – сливаются два объекта с наименьшими частотами. В результате слияния получается новый объект (внутренняя вершина), частота которого считается равной сумме частот двух сливаемых объектов. Эта вершина заносится в очередь. Huffman (C) 1. n ←│C│ │ C │- мощность С 2. Q ← C Q – очередь с приоритетами 3. for i ← 1 to n-1 4. do z ← Create_Node () z – узел, состоящий из полей f, left, right 5. x ← left [z] ← Dequeue (Q) 6. y ← right [z] ← Dequeue (Q) 7. f[z] ← f[x] + f[y] 8. Enqueue (Q, z) 9. return Dequeue (Q) вернуть корень дерева
Оценка Очередь реализована в виде двоичной кучи. Создать очередь можно за O(n). Алгоритм состоит из цикла, который выполняется n-1 раз. Каждая операция с очередью выполняется за O(log n). Общее время работы O(n log n).
Проблема построения сети Области возникновения: коммуникационные и дорожные сети. Дано: множество узлов сети (хосты, города). Необходимо: построение сети с наименьшим общим весом ребер (длина сетевых кабелей, длина дорог). Графовая модель: узлы сети являются узлами графа, E = V2, нам известны веса всех ребер. Результат: свободное дерево.
Подход к поиску МОД Строим дерево A путем добавления по одному ребру, и перед каждой итерацией текущее дерево является подмножеством некоторого МОД. На каждом шаге алгоритма мы определяем ребро (u, v), которое можно добавить к А без нарушения этого свойства. Мы назовем такое ребро безопасным
GenericMST(G, w) 1 A ← 0 2 while A не является МОД 3 do Найти безопасное для A ребро (u, v) 4 A ← A U {(u, v)} 5 return A ____________________________________________________________________________ Классификация ребер 1. Ребра деревьев (tree edges) — это ребра графа G. Ребро (u, v) является ребром дерева, если при исследовании этого ребра открыта вершина v. 2. Обратные ребра (back edges) — это ребра (u,v), соединяющие вершину u с ее предком v в дереве поиска в глубину. Ребра-циклы, которые могут встречаться в ориентированных графах, рассматриваются как обратные ребра. 3. Прямые ребра (forward edges) — это ребра (u,v), не являющиеся ребрами дерева и соединяющие вершину u с ее потомком v в дереве поиска в глубину. 4. Перекрестные ребра (cross edges) — все остальные ребра графа. Они могут соединять вершины одного и того же дерева поиска в глубину, когда ни одна из вершин не является предком другой, или соединять вершины в разных деревьях. Алгоритм DFS можно модифицировать так, что он будет классифицировать встречающиеся при работе ребра. Ключевая идея заключается в том, что каждое ребро (u, v) можно классифицировать при помощи цвета вершины v при пер- первом его исследовании (правда, при этом не различаются прямые и перекрестные ребра).
Первый случай следует непосредственно из определения алгоритма. Рассматривая второй случай, заметим, что серые вершины всегда образуют линейную цепочку потомков, соответствующую стеку активных вызовов процедуры DFS_Visit; количество серых вершин на единицу больше глубины последней открытой вершины в дереве поиска в глубину. Исследование всегда начинается от самой глубокой серой вершины, так что ребро, которое достигает другой серой вершины, достигает предка исходной вершины. В третьем случае мы имеем дело с остальными ребрами, не подпадающими под первый или второй случай. Можно показать, что ребро (u, v) является прямым, если d [u] < d [v], и перекрестным, если d [u] > d [v] ___________________________________________________________________________ Топологическая сортировка В графе предшествования каждое ребро (u, v) означает, что u предшествует v Топологическая сортировка графа есть построение последовательности а, где для всех ai и aj выполняется $(аi,аj) Þ i < j. Топологическая сортировка (topological sort) ориентированного ациклического графа G = (V, Е) представляет собой такое линейное упорядочение всех его вершин, что если граф G содержит ребро (u,v) то u при таком упорядочении располагается до v (если граф не является ацикличным, такая сортировка невозможна). Топологическую сортировку графа можно рассматривать как такое упорядочение его вершин вдоль горизонтальной линии, что все ребра направлены слева направо.
Отсортированная последовательность: C2, C6, C7, C1, C3, C4, C5, C8 TopSort(G) { for each(u in V) color[u] = white; // initialize L = new linked_list; // L is an empty linked list for each (u in V) if (color[u] == white) TopVisit(u); return L; // L gives final order } TopVisit(u) { // start a search at u color[u] = gray; // mark u visited for each (v in Adj(u)) if (color[v] == white) TopVisit(v); Append u to the front of L; // on finishing u add to list } T (n) = Θ(V + E)
Процедуры Create — Set (u) - создать множество из одной вершины u. Find — Set (u) - найти множество, которому принадлежит вершина u возвращает, в каком множестве находится указанный элемент. На самом деле при этом возвращается один из элементов множества (называемый представителем или лидером). Этот представитель выбирается в каждом множестве самой структурой данных (и может меняться с течением времени, а именно, после вызовов Union). Если вызов Find — Set для каких-то двух элементов вернул одно и то же значение, то это означает, что эти элементы находятся в одном и том же множестве, а в противном случае — в разных множествах. Union (u,v) - объединить множества, которые содержат вершины u и v Множества элементов будем хранить в виде деревьев: одно дерево соответствует одному множеству. Корень дерева — это представитель (лидер) множества. При реализации это означает, что мы заводим массив parent, в котором для каждого элемента мы храним ссылку на его предка в дерева. Для корней деревьев будем считать, что их предок — они сами (т.е. ссылка зацикливается в этом месте). Чтобы создать новый элемент (операция Create — Set), мы просто создаём дерево с корнем в вершине v, отмечая, что её предок — это она сама. Чтобы объединить два множества (операция Union(a,b)), мы сначала найдём лидеров множества, в котором находится a, и множества, в котором находится b. Если лидеры совпали, то ничего не делаем — это значит, что множества и так уже были объединены. В противном случае можно просто указать, что предок вершины b равен f (или наоборот) — тем самым присоединив одно дерево к другому. Наконец, реализация операции поиска лидера (Find — Set(v)) проста: мы поднимаемся по предкам от вершины v, пока не дойдём до корня, т.е. пока ссылка на предка не ведёт в себя. Эту операцию удобнее реализовать рекурсивно. Эвристика сжатия пути Эта эвристика предназначена для ускорения работы Find — Set(). Она заключается в том, что когда после вызова Find — Set(v) мы найдём искомого лидера p множества, то запомним, что у вершины v и всех пройденных по пути вершин — именно этот лидер p. Проще всего это сделать, перенаправив их parent на эту вершину p. Таким образом, у массива предков parent смысл несколько меняется: теперь это сжатый массив предков, т.е. для каждой вершины там может храниться не непосредственный предок, а предок предка, предок предка предка, и т.д. С другой стороны, понятно, что нельзя сделать, чтобы эти указатели parent всегда указывали на лидера: иначе при выполнении операции Union пришлось бы обновлять лидеров у O(n) элементов. Таким образом, к массиву parent следует подходить именно как к массиву предков, возможно, частично сжатому. Применение эвристики сжатия пути позволяет достичь логарифмическую асимптотику: на один запрос в среднем Анализ Инициализация – O(V) Цикл выполняется V раз и каждая операция extractMin выполняется за - O(logV) раз, всего O(V logV) раз Цикл for выполняется O(E) раз, decreaseKey - за время O(logV). Общее время работы - O(V log V +E logV)= O(E logV)
Свойство кратчайшего пути Пусть p = (v1, v2..... vk) - кратчайший путь из вершины v1 к вершине vk в заданном взвешенном ориентированном графе G = (У. Е) с весовой функцией w: Е → R a pij = (vi, vi+1.....vj) - частичный путь пути p, который проходит из вершины vi к вершине vj для произвольных i и j (1 ≤ i < j ≤ k). Тогдa pij – кратчайший путь из вершины vi к vi Dijkstra(G, w, s) { for each (u in V) { // initialization d [u] = +infinity color [u] = white pred[u] = null } d[s] =0 // dist to source is 0 Q = new PriQueue(V) // put all vertices in Q while (Q.nonEmpty()) { // until all vertices processed u = Q.extractMin(} // select u closest to s for each (v in Adj[u]) { if (d[u] + w(u,v) < d[v]) { // Relax(u,v) d [v] = d [u] + w(u,v) Q.decreaseKey(v, d[v]) pred [v] = u } } color [u] = black } [The pred pointers define an '1 inverted'' shortest path tree] }
Оценка сложности Алгоритм Беллмана-Форда завершает свою работу в течение времени O(V*E), поскольку инициализация в строке 1 занимает время O(V), на каждый из |V| — 1 проходов по ребрам в строках 2-4 требуется время в O(E), а на выполнение цикла for в строках 5-7 — время O(Е)..
Асимптотическая оценка алгоритма • Анализ алгоритмов – теоретическое исследование производительности компьютерных программ и потребляемых ими ресурсов. • Быстродействие – время работы алгоритма, в зависимости от объема входных данных. • Определяется функцией Т(n), где n – объем входных данных Виды анализа • Наихудший случай: T(n) – максимальное время для любых входных данный размера n. • Средний случай: T(n) – ожидаемое время для любых входных данных размера n. • Наилучший случай – минимальное время работы. Асимптотическая оценка O - нотация: асимптотическая верхняя граница f (n) = O(g(n)) Þ ($c > 0, n0> 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n0) O(g(n)) = {f (n): $ c > 0, n0 > 0 Þ 0 ≤ f (n) ≤ c · g(n), n ≥ n0} Пример: 2n2 = O(n3)
Ω - нотация: асимптотическая нижняя граница Ω(g(n)) = {f (n): $c > 0, n0 > 0 Þ 0 ≤ c · g(n) ≤ f (n), n ≥ n0}
Пример 1 f(n)=1/2n2-3n Докажем, что g(n)=n2 является асимптотической оценкой f(n)
При С2= 1/2 неравенство будет выполнятся (n→∞) n0=7, так как n=6 брать нельзя (С1и С2>0) C1= 1/14, С2= 1/2 из выражения – 1/2-3/7=1/14. Утверждение верно Пример 2 f(n)=6n3
Асимптотические оценки: θ(1), θ(log2n), θ(n), θ(n*log2n), θ(n2), θ(n3), θ(2n)
Методика оценки не рекурсивных алгоритмов. Пример
Рекурсивные алгоритмы, построение асимптотической оценки. Пример Сортировка слиянием sort(А,p,r) //p - начало массива, r – конец массива T(n) { if(p < r) //1 { q=(p + r)/2; //Вычисляем середину массива 1 sort(А,p,q); //сортируем левую часть T(n/2) sort(А,q+1,r); //сортируем правую часть T(n/2) merge(p,q,r); //сливаем два массива в один n } }
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.014 с.) |


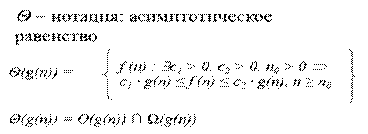
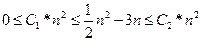 f(n)=θ(n2)
f(n)=θ(n2)
 Докажем, что g(n)=n2 является асимптотической оценкой f(n)
Докажем, что g(n)=n2 является асимптотической оценкой f(n)  f(n)=θ(n2)
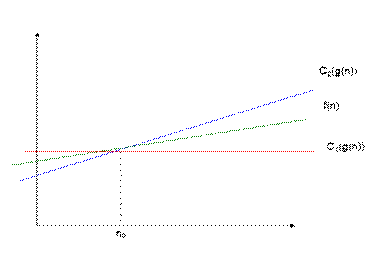
f(n)=θ(n2) Предположение неверно т.к. не выполняется условие
Предположение неверно т.к. не выполняется условие


 = = n + (n-1) + (n-2)…+2 =
= = n + (n-1) + (n-2)…+2 =  -1
-1 = (n-1) + (n-2)…+1 =
= (n-1) + (n-2)…+1 = 




 n2 n2
n2 n2




 (n/2)2 (n/2)2 log n (1/2)*n2
(n/2)2 (n/2)2 log n (1/2)*n2 (n/4)2 (n/4)2 (n/4)2 (n/4)2 (1/4)*n2
(n/4)2 (n/4)2 (n/4)2 (n/4)2 (1/4)*n2 T (n) = 2T (n/2) + n
T (n) = 2T (n/2) + n





 h(51) = h(49) = h(63) = i
h(51) = h(49) = h(63) = i

 Число проб при успешном поиске
Число проб при успешном поиске