
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение удельного сопротивления исходного кристаллаСодержание книги
Поиск на нашем сайте
Удельное, сопротивление исходного кристалла влияет на ряд параметров выпрямительного диода: прямое падение напряжения, обратный ток, емкость и т. д. Но в наибольшей степени от него зависит напряжение лавинного пробоя p — n-перехода UB, поэтому выбор удельного сопротивления исходного кристалла производится то напряжению лавинного пробоя. Напряжение лавинного пробоя определяется по заданному значению повторяющегося импульсного обратного напряжения Urrm [1]:
где k — коэффициент запаса. Значение коэффициента запаса выбирается равным 0,75 — 0,80 [1]. Напряжение лавинного пробоя диффузионного р — n-перехода зависит не только от удельного сопротивления исходного кристалла, но и от характера распределения диффундирующей примеси. Примесные профили диффузионных (особенно высоковольтных) р — n-переходов, в пределах области объемного заряда наиболее точно аппроксимируются экспонентой [1]. Тогда результирующая примесная концентрация, например, для случая диффузии акцепторной примеси в исходный материал n-типа, имеет вид:
где xj — глубина залегания р — n-перехода от поверхности; N0, λ - параметры аппроксимации. Подбирая параметры экспоненциального распределения, можно с высокой точностью аппроксимировать реальное распределение примесей в районе металлургического перехода. Наиболее просто и легко это можно сделать, приравняв градиенты концентраций реального примесного профиля и аппроксимирующей (экспоненциальной) функции в плоскости металлургического р — n-перехода (при x = хj). Если, например, диффузия проводится из ограниченного источника, то получаем:
Здесь xj определяется из выражения
где D — коэффициент диффузии примеси; t — время диффузии; Q —количество атомов диффундирующей примеси, приходящейся на единицу площади; N0 — концентрация легирующей примеси в исходном кристалле. При диффузии из источника с постоянной концентрацией диффундирующей примеси параметр λ находится по формуле
где Ns— поверхностная концентрация диффундирующей примеси. Между параметрами аппроксимации λ и N0 имеется связь:
где a — градиент концентрации диффундирующей примеси в плоскости металлургического перехода. Напряжение лавинного пробоя экспоненциального перехода с диффузионным профилем (1.2.2) можно вычислить с помощью соотношения, получаемого из решения уравнения Пуассона [1]:
где lB - ширина области объемного заряда (ООЗ) при напряжении пробоя. Для кремниевых экспоненциальных р — n-переходов lB определяется следующими выражениями:
Указанные соотношения определяют ширину области объемного заряда р - n-перехода при пробое с погрешностью менее 5 %. В приближении экспоненциального перехода концентрацию легирующей примеси (а значит, и удельное сопротивление) исходного кристалла можно определить следующим образом: Сначала по соотношениям (1.2.3) и (1.2.5) исходя из предпочтительных значений величин хj и Dt в первом приближении определяют величину λ. для выпрямительных диодов при обычно используемых режимах диффузии она составляет от 0,5 до 15,0 мкм. Малые значения λ характерны для неглубоких р — n-переходов, получаемых кратковременной диффузией. Однако в них трудно осуществить защиту от поверхностного пробоя. Переходы с очень высокими значениями λ требуют длительных диффузий и имеют большую глубину залегания от поверхности, что обычно тоже нецелесообразно. Поэтому, если нет каких-либо ограничений, λ выбирается из середины приведенного выше интервала. Затем определяется ширина области объемного заряда р — n-перехода при напряжении лавинного пробоя. В кремниевых диффузионных р — n-переходах независимо от профиля легирования в широком диапазоне напряжений пробоя имеют место следующие приближенные соотношения [1]:
В этих выражениях UB задается в вольтах, а lB получается в микрометрах. После определения lB и λ в первом приближении из соотношений (1.2.8а), (1.2.8б) рассчитывается значение концентрации легирующей примеси в исходном материале N0. Имея значения параметров lB, λ и N0 в первом приближении, по выражению (1.2.7) можно уточнить напряжение лавинного пробоя экспоненциального p—n-перехода. Если расхождение между полученным и требуемым значениями составляет меньше З %, то расчет на этом можно заканчивать. Если же оно оказывается больше, то необходимо скорректировать параметры N0 или λ. Для повышения напряжения пробоя р — n-перехода можно увеличивать λ или уменьшать N0. После коррекции параметров N0 и λ по (1.2.8а), (1.2.8б) находят новое значение lB и по (1.2.7) — напряжение лавинного пробоя. После окончания определения с помощью выражений (1.2.3) — (1.2.5) следует оценить значения хj и Dt, необходимые для получения рассчитываемого р –n-перехода. Если они приемлемы, т. е. их можно получить в обычном технологическом процессе без особых затруднений, процесс нахождения N0 можно считать законченным и установить удельное сопротивление исходного материала.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 , (1.2.1)
, (1.2.1) , (1.2.2)
, (1.2.2) (1.2.3)
(1.2.3) , (1.2.4)
, (1.2.4) , (1.2.5)
, (1.2.5) , (1.2.6)
, (1.2.6) , (1.2.7)
, (1.2.7) (для lB ≤ 5λ); (1.2.8а)
(для lB ≤ 5λ); (1.2.8а)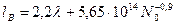 (для lB > 5λ). (1.2.8б) где lB и λ в микрометрах, а N0 в см-3.
(для lB > 5λ). (1.2.8б) где lB и λ в микрометрах, а N0 в см-3. (для 30 ≤ UB ≤ 300 В), (1.2.9а)
(для 30 ≤ UB ≤ 300 В), (1.2.9а)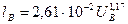 (для UB ≥ 300 В). (1.2.9б)
(для UB ≥ 300 В). (1.2.9б)


