Движение жидкой среды в рабочем колесе центробежного насоса. Параллелограммы и треугольники скоростей.

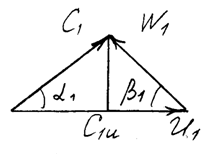
Жидкая среда к рабочему колесу насоса подводится в осевом направлении, и каждая ее частичка движется поступательно, с абсолютной скоростью С. Попав в межлопаточное пространство колеса каждая из них принимает участие в сложном движении.Движение частицы 1, вращающейся вместе с колесом, характеризуется вектором окружной (переносной) скорости U,.направленным перпендикулярно к радиусу вращения (или по касательной к окружности вращения). Кроме того, эта же частица перемещается относительно колеса и характеризуется вектором относительной скорости W, направленным по касательной к линии тока в относительном потоке (поскольку линия тока в относительном потоке совпадает с поверхностью лопатки, вектор относительной скорости будет направлен по касательной к поверхности лопатки). Абсолютное движение частицы 1 характеризуется вектором абсолютной скорости, равным геометрической сумме векторов окружной и относительной скоростей, т. е. C=U+W. Таким образом,в любой точке межлопаточного канала колеса можно построить треугольник (или параллелограмм) скоростей. Для рассмотрения кинематики потока при движении.жидкой среды в рабочем колесе принято строить треугольники скоростей на входной 1 и выходной 2 кромках лопатки, предполагая: при этом, что во всех точках сечений на входе в рабочее колесо и на выходе из него треугольники скоростей будут такими же.

 

 

 

Ua– вектор окружной скорости

Wa– вектор относительной скорости

Са – вектор абсолютной скорости

 

Основное уравнение работы центробежного насоса.

Учесть все явления, происходящие в рабочем колесе, при выводе основного уравнения работы насоса не представляется возможным. Поэтому примем следующие допущения.

1. Условное рабочее колесо имеет бесконечно большое число (z=∞) бесконечно тонких лопаток. Тогда можно считать, что между лопатками будут элементарные потоки — струйки, и относительное движение в таких элементарных каналах можно характеризовать одним вектором скорости. Следовательно, при z=∞ все струйки в цилиндрических сечениях колеса имеют одинаковыетреугольники скоростей и энергию.

2. Жидкая среда, подаваемая условным рабочим колесом, идеальна, т. е. совершенно несжимаема, и в ней отсутствуют силы вязкости.

При закрытой задвижке работа насоса затрачивается на создание напора, который выражается следующей формулой: (2) (1), где H_T – теоретический напор (число лопаток бесконечно)

При открытой задвижке насоса затрачивается на создание напора:

(3)

(4)

Подставляем выражение (4) в выражение (3) и получаем:

Виды лопаток рабочего колеса центробежного насоса и влияние их формы на напор.

Существуют три вида лопаток: загнутые (по ходу вращения) назад (рис. 1); с радиальным выходом (рис. 2); загнутые вперед (рис. 3).

При равных геометрических размерах колес и постоянном значении U₂ с возрастанием β₂ увеличивается окружная составляющая (C_U2) абсолютной скорости. Следовательно, на основании основного уравнения можно сделать вывод, что с увеличением угла β₂ напор насоса увеличивается и у рабочего колеса с лопатками, загнутыми вперед, он будет наибольшим. Однако в практике насосостроения чаще всего используются рабочие колеса с лопатками, загнутыми назад. Это объясняется следующими причинами. Более совершенным является насос с большим коэффициентом статического напора.

 

β2<90 β2=90 β2>90

Идеальная и действительная подачи центробежного насоса

Идеальная подача насоса без учёта стеснения потока лопатками определяется как произведение площади сечения на выходе из рабочего колеса на радиальную составляющую абсолютной скорости (так как эта составляющая нормально к площади сечения):

С учётом стеснения потока лопатками:

Действительная подача насоса отличается от теоретической объёмными потерями:

Явление кавитации в насосах

Теоретически при условии и геометрическая высота всасывания . Однако в реальных условиях её предельное значение ниже по следующим причинам. Во всасывающем трубопроводе при понижении давления до критического значения (в практических расчетах за критическое давление принимают давление насыщенного пара при данной температуре перекачиваемой жидкости) из жидкой среды начинают выделяться пузырьки пара и растворённого в ней газа. Увлекаясь далее потоком в область повышенного давления, пар конденсируется и пузырьки захлопываются. Описанное явление называется кавитацией.

Конденсация пара происходит за очень короткий промежуток времени, и при захлопывании пузырьков в результате гидравлических ударов возникают ударные волны. При многократном воздействии ударных волн обтекаемая жидкой средой поверхность разрушается, т.е. происходит кавитационная эрозия. Поверхность становится пористой, параметры шероховатости её увеличиваются. Особенно сильно кавитационной эрозии подвержены чугун и углеродистая сталь, наиболее устойчивы нержавеющая сталь и бронза. При возникновении кавитации нарушается сплошность потока, что приводит к резкому снижению напора, подачи и КПД. Кроме того, работа насоса в кавитационном режиме сопровождается характерным потрескивающим шумом и вызывает вибрацию установки.

При расчете предельной геометрической высоты всасывания необходимо исключать условия возникновения кавитации, чтобы не возникла кавитация, полный напор на всасывающей стороне насоса должен быть больше напора насыщенного пара при данной температуре на значение кавитационного запаса :