
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Горение капли жидкого топливаСодержание книги
Поиск на нашем сайте
Имея в виду, что горение жидких топлив происходит в паровой фазе, процесс горения капли жидкого горючего можно представить следующим образом. Капля жидкого топлива окружена атмосферой, насыщенной парами этого горючего. Вблизи от капли по сферической поверхности с диаметром d 2устанавливается зона горения. Химическое реагирование смеси паров жидкого топлива с окислителем происходит весьма быстро, поэтому зона горения весьма тонка. Скорость горения определяется наиболее медленной стадией-скоростью испарения горючего. В пространстве между каплей и зоной горения находятся пары жидкого топлива и продукты горения. В пространстве вне зоны горения- воздух и продукты сгорания. В зону горения изнутри диффундируют пары топлива, а снаружи - кислород. Здесь эти компоненты смеси вступают в химическую реакцию, которая сопровождается выделением тепла. Из зоны горения тепло переносится наружу и к капле, а продукты сгорания диффундируют в окружающее пространство и в пространство между зоной горения и каплей (рис.9). Однако механизм передачи тепла еще не представляется ясным. Ряд исследователей считает, что испарение горящей капли происходит за счет молекулярного переноса тепла через пограничную застойную пленку у поверхности капли.
Помере выгорания капли из-за уменьшения поверхности общее испарение уменьшается, зона горения суживается и исчезает при полном выгорании капли. Так протекает процесс горения капли полностью испаряющихся жидких топлив, находящейся в покое в окружающей среде или движущейся вместе с ней с одинаковой скоростью. Количество кислорода, диффундирующее к шаровой поверхности при прочих равных условиях, пропорционально квадрату ее диаметра, поэтому установление зоны горения на некотором удалении от капли обусловливает большую скорость ее горения по сравнению с такой же частицей твердого топлива, при горении которой химическая реакция практически протекает на самой поверхности. Так как скорость горения капли жидкого топлива определяется скоростью испарения, то время ее выгорания можно рассчитать на основе уравнения теплового баланса ее испарения за счет тепла, получаемого из зоны горения, т. е.
где q - количество тепла, получаемое из зоны горения едини- цей поверхности капли в единицу времени, кВт/м2; F - поверхность капли в текущий момент времени, м2; τ - время полного выгорания капли, с; ρ - плотность жидкого горючего, кг/м3; сср - средняя теплоемкость жидкого топлива, кДж/(кгК); г и
кого топлива, °С; λп - теплота испарения, кДж/кг; Уменьшение объема капли за промежуток времени τ и текущий r и начальный rо радиус капли, время полного выгорания капли жидкого горючего можно определить согласно уравнению (10-4).
Использование формулы (10-5) для расчета времени выгорания жидкого топлива связано с трудностями определения теплового потокаq, поступающего из зоны горения к поверхности капли. Для того чтобы показать определяющую роль испарения в протекании процесса горения капли и зависимость испарения от тепловых условий Л. Н. Хитрин рассмотрел предельный случай, когда горение паров не лимитирует процесс, а тепловые условия задаются независимо от процесса горения паров горючего вблизи от поверхности капли. Им изложен метод определения количества тепла, получаемого движущейся каплей в предположении, что теплообмен капель с окружающей средой совершается только конвекцией. В этом случае тепловой поток, воспринимаемый каплей, ранен:
где Тс - температура окружающей среды. Величина коэффициента теплоотдачи αс зависит от состояния движерия среды и рассчитывается по зависимости критерия Nu от числа Rе, определяемой экспериментально. Для мелких капель, движущихся в потоке с очень малой относительной скоростью (Rе<100), критерий
откуда Подставив выражение (3.4) для q с учетом выражения (3.5) формулу (3.3) и проинтегрировав, получим:
Согласно формуле (3.6) продолжительность выгорания капли, испаряющейся в процессе конвективного нагрева в несущем газовом потоке, пропорциональна квадрату ее начального радиуса. Поскольку горение капель удовлетворяет линейной зависимости квадрата диаметра испаряющейся или горящей в диффузионном режиме капли от времени, то как характерную величину для горения капли принимают коэффициент горения
При горении в воздухе с температурой 800-900°С и скоростях обтекания капель до 1 м/с для бензина К =1,3-*-1,5; для керосина К= 1,0 -1,3 мм2/с, для мазута и солярового масла значение к приблизительно такое же. Коэффициент к возрастает с повышением температуры среды и концентрации кислорода, которые приводят к повышению температуры в зоне горения, а также с ростом скорости обтекания капли, приводящим к увеличению величины критерия Nu. При сравнительно крупных каплях увеличивается расстояние от поверхности капли до зоны горения, вследствие чего роль конвективного теплообмена с каплей уменьшается и начинает превалировать передача тепла излучением из зоны горения. В этом случае тепловой поток, воспринимаемый каплей, согласно может быть принят равным q = qл (3.8) где qл — интенсивность излучения диффузионного пламени на поверхности капли. Подставив эту величину в выражение (3.3) получим формулу для расчета времени выгорания капли при условии лучистого теплообмена
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.83.204 (0.007 с.) |

 Рис. 9. Схема горения капли жидкого топлива
Рис. 9. Схема горения капли жидкого топлива
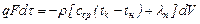 , (3.2)
, (3.2)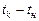 - температура кипения и начальная температура жид
- температура кипения и начальная температура жид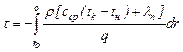 (3.3)
(3.3)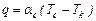 (3.4)
(3.4)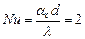 ,
,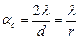 (3.5)
(3.5)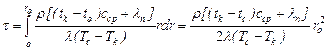 (3.6)
(3.6)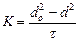 , мм2/с (3.7)
, мм2/с (3.7)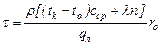 (3.9)
(3.9)


