
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Транзисторный каскад с общим эмиттером.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Биполярные транзисторы чаще всего используются в усилительных каскадах. На рис.17 изображен транзисторный каскад с общим эмиттером. Режим работы биполярного транзистора в каскаде определяется силой базового тока. Для того чтобы базовый ток был стабилен, база соединяется с источником питания схемы Е Кчерез высокоомное сопротивление RБ.
Е К – постоянное напряжение питания транзисторного усилителя. Полярность источника питания усилительного каскада зависит от типа выбранного транзистора. R н – сопротивление нагрузочного устройства; Резистор R б., обеспечивает требуемую работу транзистора в режиме покоя усилителя, то есть в отсутствие входного сигнала. Резистор R к – резистор в цепи отрицательной обратной связи по току коллектора, вместе с R н определяет величину выходного сигнала, задает линию нагрузки на семействе выходных характеристик транзистора, определяет выбор начальной рабочей точки в режиме покоя, напряжение покоя U к.э. п и ток покоя I к. п транзистора. Разделительный конденсатор C р. 1 передает на вход усилителя переменную составляющую сигнала от источника uвх., не пропуская постоянный ток от источника питания Е к во входную цепь усилителя. Разделительный конденсатор C р. 2 передает на выход усилителя переменную составляющую сигнала, не пропуская постоянный ток от источника питания Е к в выходную цепь усилителя, тем самым уменьшается потребление мощности усилителя от источника питания и исключаются искажения сигнала на выходе усилительного каскада. Таким образом, разделительные конденсаторы отделяют усилительный каскад от входной и выходной цепей схемы. Для определения режима работы транзисторного каскада удобно построить линию нагрузки на характеристиках транзистора. Данный способ позволяет описать поведение транзистора во всех основных режимах работы, а именно: насыщения, усиления и отсечки.
Режим насыщения транзистора имеет место в случае, когда ток коллектора не управляется током базы. Такая ситуация возникает при условии h21э.IБ >IKH, где IKH - ток насыщения коллектора.
IН.К. = В режиме усиления ток коллектора должен быть меньше тока насыщения 1КН. Значение тока коллектора и соответствующее ему напряжение коллектор-эмиттер задает рабочая точка на нагрузочной прямой (например, точка 1). Значение резистора RК. можно рассчитать: Значение тока базы:
Сопротивление в цепи базы:
Напряжение UБ.Э. определяется из входной ВАХ транзистора.
В режиме отсечки ток коллектора равен нулю и не создает на резисторе RK падения напряжения. Следовательно, напряжение UKЭ максимально и равно напряжению источника питания ЕK. Данный режим соответствует точке 2. При работе транзисторного каскада в режиме малого сигнала обеспечивается наибольшее усиление входного сигнала при минимальных искажениях. Характерной особенностью данного режима является то, что при всех возможных значениях входного сигнала рабочая точка транзистора не выходит из линейной области. При поступлении на вход усилителя переменного сигнала uВХ., ток базы транзистора (согласно ВАХ) тоже будет изменяться. Изменение тока базы вызовет изменение коллекторного тока. Последний вызовет изменение выходного напряжения усилителя, причем выходное напряжение будет в КU раз больше входного. То есть произойдет усиление входного сигнала.
КU = ΔUВЫХ/ΔUВХ.
Важной характеристикой усилителя является амплитудно-частотная характеристика – зависимость коэффициента усиления усилителя от частоты усиливаемого сигнала. Величина коэффициента усиления снижается на низких частотах – из-за конденсаторов, входящих в состав схемы; и верхних частотах – из-за частотных свойств транзистора. Также от частоты зависит и угол сдвига фаз между выходным и входным напряжениями. Такая характеристика называется фазо-частотной.
Полоса пропускания усилителя Δ F = f в.гр – f н.гр.
Логические элементы.
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Логические элементы широко применяются в автоматике, вычислительной технике и цифровых измерительных приборах. Логические элементы создают на базе электронных устройств, работающих в ключевом режиме – на диодах, транзисторах. Логическим элементом называется физическое устройство, реализующее какую-либо из функций алгебры логики (булевой алгебры) над переменными (аргументами), поступающими на его входы. Аргументы и функции представляются в двоичной форме: в виде нулей и единиц. Высокий уровень сигнала соответствует логической единице (1), а низкий – логическому нулю (0). Любую логическую функцию удобно представить в виде таблицы состояний (таблицы истинности), где указываются возможные комбинации аргументов и соответствующие им функции. Для логического элемента с двумя входами можно реализовать следующие функции:
Система логических функций называется функционально полной, если используя только эти функции можно реализовать любые другие. Функционально полными являются системы: 1) “и”, ”или”, ”не”, 2) “и”, ”не”, 3) “или”, ”не”. Это можно доказать, используя законы булевой алгебры.
Законы булевой алгебры.
В базовых элементах одной серии используется одинаковая микросхемная реализация. Серия характеризуется общими электрическими, конструктивными и технологическими параметрами.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 662; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.252.215 (0.01 с.) |



 .
.



 ù x
ù x














 =1
=1
 = х
= х
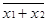 =
= 




