Общая задача оптимизации и задача оптимизации управляемых процессов

Исходная информация для решения задач оптимального управления содержится в постановке задачи. Задача управле­ния может формулироваться в содержательных (неформальных) терминах, которые часто носят несколько расплывчатый характер. Для применения математических методов необходима четкая и строгая формулировка задач, которая бы устраняла возможные неопределенности и двусмысленности и одновременно делала бы задачу математически корректной. С этой це­лью для обшей задачи необходима адекватная ей математическая формулировка, называемая математической моделью зада­чи оптимизации.

Математическая модель (ММ) - достаточно полное математическое описание динамической системы и процесса управ­ления в рамках выбранной степени приближения и детализации.

ММ отображает исходную задачу в некоторую математическую схему, в конечном итоге - в некоторую систему чисел. В ней, с одной стороны, явно указываются (перечисляется) все сведения, без которых невозможно приступить к аналитиче­скому или численному исследованию задачи, а с другой, – т.е. дополнительные сведения, которые вытекают из сущности за­дачи и которые отражают определенное требование к ее характеристикам.

Первая задача, которая возникает при управлении системой, – выбор таких воздействий на систему, чтобы проис­ходящий процесс удовлетворял заданным условиям. Подобные процессы принято называть допустимыми.

Решение этой задачи неоднозначно. Допустимые процессы в системе образуют множество. Тогда возникает следующая задача – выбор из этого множества процесса, который является в некотором смысле наилучшим Другими словами, это задача выбора оптимального процесса.

Чтобы решать оптимизационные задачи с помощью мате­матических методов, нужно, прежде всего, сформулировать на математическом языке рассматриваемые процессы и их математические модели. Далее требуется дать математическое выражение понятию «наилучший» – свойству, которым должен обладать искомый процесс. Наконец, необходимо с помощью математических средств уметь отразить те ограничения, которые накладываются на состояние системы и управления.

В общем виде задача оптимизации формулируется как задача отыскания минимального (или максимального) значения функ­ционала на множестве М. Эта задача ставится аналогично задаче об отыскании экстремума функции.

Задачи оптимального управления представляют собой важный класс задач оптимизации. Эти задачи являются частными по отношению к сформулированной выше общей задаче оптимизации.

Необходимость управлять процессом оптимально, т. е. на­илучшим в определенном смысле образом, возникает в системах, характеристики которых меняются во времени под влиянием управлений. К такому классу систем относится и экономическая система. Для того чтобы сформулировать на математическом языке задачу управления в таких системах, необходимо ввести некоторые понятия и построить соответствующую математи­ческую модель.

Важнейшими понятиями в теории оптимального управления являются понятия состояния системы и управления. Будем рассматривать системы, состояние которых может быть в любой момент времени определено вектором х п-мерного векторного пространства с координатами . Пространст­во Х будем называть пространством состояний системы.

Так как система изменяется во времени, то ее поведение можно описать последовательностью состояний. Такую последовательность системы называют траекторией системы.

Переменную t, которая является независимой, назовем аргу­ментом процесса. Аргументом процесса может быть любая величина, но чаще всего – время. Переменная t может пробегать некоторый отрезок числовой прямой, если , или отрезок натурального ряда . В первом случае процесс, происходящий в системе, называется непрерывным, во втором случае – многошаговым. Системы в этих случаях назовем соот­ветственно непрерывными и дискретными.

Изменение состояния системы, т. е. процесс в ней, может происходить под воздействием управляющих воздействий. Будем рассматривать системы, управляющие воздействия в которых моделируются с помощью элементов r-мерного векторного про­странства U:

Управляющие воздействия могут задаваться в виде функций от t. Тем самым реализуется определенный способ управления системой. В этом случае будем говорить о задании программы

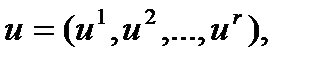
На возможные (допустимые) состояния системы x(t) и управ­ления и u(t) могут быть наложены ограничения. Рассмотрим множество троек – совокупность (n+r+1) – мерных векто­ров в пространстве . Тогда ограничения на состояние системы и управления в самом общем случае могут быть записаны в виде

,

где – некоторая область (подмножество) рассматриваемого (n+r+1) – мерного пространства. Ограничения на величины x(t), u(t) в каждый фиксированный момент времени t могут быть заданы и в виде

где – сечение множества V при заданном t.