
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы расчета изгибаемых элементовСодержание книги
Поиск на нашем сайте
Для изгибаемых элементов (балок), у которых пролет превышает высоту поперечного сечения (в 5 и более раз) изменение деформаций по высоте сечения происходит по линейному закону, напряжения распределяются только до предела текучести ƠT (рис.2.1). Напряжения в точках, находящихся на расстоянии “y” от нейтральной оси, определяются по формуле Ơ = М y / Ix, где Максимальное напряжение возникает когда Точки сечения Для проверки прочности изгибаемых элементов, работающих в пределах упругих деформаций, необходимо, чтобы максимальные нормальные и касательные напряжения в балке от расчетной нагрузки не превосходили соответствующих расчетных сопротивлений.
Рис.2.1. Изменение эпюры напряжений в изгибаемом элементе при развитии Пластических деформаций в материале
τ = Q S /I t≤ Rs
где
По второму предельному состоянию наибольший прогиб балки от нагрузки при эксплуатации сравнивается с предельной величиной указанной в нормах, либо в задании на проектирование. Величина прогиба зависит от расчетной схемы балки, а предельный прогиб – от назначения. Например, для главной балки рабочей площадки промздания, имеющей один пролет и шарнирные опоры, загруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле:
5 fmax = ----- (qn l4 / E I) ≤ l / 400 (2.11) 384
где
Формула для проверки прочности изгибаемых элементов при наличии пластических деформаций (пластический шарнир) получается из выражения (2.10) путем замены
M / (c Wn) ≤ Ry γc или M / Wn ≤ cRy γc (2.12).
Сравнивая это выражение с (2.10) видим, что формально учет пластических деформаций сводится к повышению расчетного сопротивления умножением на величину “c”, коэффициент, характеризующий резерв несущей способности изгибаемого элемента, обусловленный пластической работой металла, и определенный по формуле для балок двутаврового сечения, как наиболее распространенного в изгибаемых элементах
где
Для прокатных двутавров различных типов Для составных двутавров (рис.2.2, в). коэффициент “c” вычисляется по формуле (2.13). Для прямоугольного сечения, когда площадь Устремляя площадь стенки к нулю (рис.2.2, е) из двутавра получаем расчетные сечения фермы или балки с гибкой стенкой, тогда с = 1. Наибольшим пластическим резервом будет обладать балка с поперечным сечением (см. рис.2.2, а), для нее с = 2. Практически выбор формы поперечного сечения изгибаемых элементов зависит от многих факторов, среди которых главным является расход металла, так как его стоимость составляет 80% общей стоимости конструкции. Кроме нормальных напряжений Ơ в балках возникают и касательные напряжения τxy, зависящие от поперечной силы будет компонента Ơx. При большей сосредоточенной нагрузке на балке с малым пролетом (рис.2.3, б) определяющим будет напряжение τxy.. Распределение Ơпр
Рис.2.2. Зависимость коэффициента “c” от формы поперечного сечения Изгибаемого элемента по высоте балки в упругой стадии будет существенно отличаться от предыдущего случая, а при дальнейшем увеличении нагрузки вплоть до появления пластического шарнира (Ơпр = ƠT) обусловит более развитую пластическую область вблизи нейтральной оси. При рассмотренном многократном напряженном состоянии проверку прочности балки можно производить по формуле:
где 1,15 – коэффициент, учитывающий развитие пластических деформаций в балке [аналогично коэффициенту “ c ” в формуле (2.12)].
При изгибе относительно двух главных осей инерции поперечного сечения балки (x, y) – косом изгибе - допускается проверку прочности. производить по упрощенной формуле
Mx/(cx
где
Рис. 2.3. Распределение пластических деформаций в двутавровой балке при сложном напряженном состоянии.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.01 с.) |

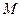 - изгибающий момент в рассматриваемом сечении балки; Ix - момент инерции сечения.
- изгибающий момент в рассматриваемом сечении балки; Ix - момент инерции сечения. : Ơmax. = М(h/2)/Ix. Отношение момента инерции Ix к расстоянию от нейтральной оси до крайней
: Ơmax. = М(h/2)/Ix. Отношение момента инерции Ix к расстоянию от нейтральной оси до крайней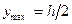 называется моментом сопротивления Wx = Ix(2/h), тогда Ơmax = M/Wx..
называется моментом сопротивления Wx = Ix(2/h), тогда Ơmax = M/Wx..

 ; (2.10)
; (2.10)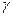 c.
c.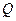 - максимальный момент и поперечная сила в балке от расчетной нагрузки;
- максимальный момент и поперечная сила в балке от расчетной нагрузки;  - момент сопротивления нетто поперечного сечения балки, в случае несимметричного сечения балки выбирается Wnmin = Ix / y max;
- момент сопротивления нетто поперечного сечения балки, в случае несимметричного сечения балки выбирается Wnmin = Ix / y max; 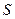 - статический момент сдвигающейся части сечения относительно нейтральной оси; I - момент инерции сечения балки;
- статический момент сдвигающейся части сечения относительно нейтральной оси; I - момент инерции сечения балки; 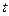 - толщина стенки.
- толщина стенки. - максимальный прогиб балки;
- максимальный прогиб балки;  - нормативная нагрузка на балку;
- нормативная нагрузка на балку;  - прогиб балки; E I - изгибная жесткость балки; 400 – норма прогиба балки.
- прогиб балки; E I - изгибная жесткость балки; 400 – норма прогиба балки.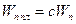 , т.е.
, т.е. , (2.13)
, (2.13) - отношение площадей поперечного сечения пояса и стенки балки.
- отношение площадей поперечного сечения пояса и стенки балки. , чему соответствует значение с = 1,1.
, чему соответствует значение с = 1,1. поясов балки можно приравнять к нулю – с = 1,5 (рис.2.2, б).
поясов балки можно приравнять к нулю – с = 1,5 (рис.2.2, б).
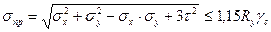 (2.14)
(2.14) Wx.n.min)+My/(cy Wy.n.min) ≤ Ry γc при τ≤ 0.5Rs (2.15)
Wx.n.min)+My/(cy Wy.n.min) ≤ Ry γc при τ≤ 0.5Rs (2.15) и
и  даются в зависимости от формы сечения (см.прил.1);
даются в зависимости от формы сечения (см.прил.1);  .
.



