
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
The real numbers. Supremum and Infimum of a set.Содержание книги
Поиск на нашем сайте Some set theory. Answer: Definition: Let S and T be set: a) S contains T, and we write S c T or T c S, if every number of T is also in S. in this case, T is a subset of S. b) S\T is the set of elements that are in S, but not in T. c) S equals T, and we write: S=T, is S contains T, and T contains S, thus, S=T if and only if S and T have the same members. d) The compecment of S denoted by Sc, is the set of elements in the universal set that are not in S. e) The union of S and T, denoted by S f) The intersection of Sand T, denoted by S Definition If x0 is real number and, ε>0, then the open interval (x0-ε,x0+ε) in an neighborhood of x0. If the set S contains an ε-neighborhood of x0, then S is a neighborhood of x0, and x0 is an interior point of S. Definition. Let S be subset of R. Then (a) x0 is a limit-point of S, if every deleted neighborhood of x0 contains a point of S. (b) x0 is boundary point of S, if every neighborhood of x0 contains a least one point in S and one not in S. The set of boundary points of S denoted by The closure of S, denoted by (c)x0 is exterior to S, of x0 is in the interior of Sc Theorem. A set Sis closed, if and only if no point of Scis a limit point of S. Corollary. A set is closed, if and only if it contains all its limit points. Definition. A collection H of open sets, is an open covering of a set S, if every point in S is contained in a set H belonging to H, that is, if Sc
Heine-borel Theorem. Bolzano-Weierstrass Theorem. Answer: If H is an open covering of a closed and bounded subset S of the real line, then S has an open covering H consisting of finitely many open sets belonging to H. Proof: Since S bounded, it has an infimumα and supremum β, and, since S is closed,α and β belong to S. Define St=S and let F={t|α<t<β and finitely many sets form H cover St} Since Sβ =S1 the theorem will be proved, if we can show that β Since α Since, F is nonempty and bounded above by β, it has supremumλ. First, we wish to show that λ=β by definition of F, it suffices to rull out the possibility that α<β. We consider two cases: Case 1. Suppose that α<β and λ However, the definition of λ implies that Sλ-ε has a finite subcovering from H, while Sλ+εdoes not. This is a contradiction. 3.2 Case 2. Suppose that λ<β and λ Now we know that α=β, which is in S. Therefore, there is an open set Hβ in H that contains β and along with, an interval of the from [β-ε,β+ε], for some positive ε. Since Sβ-ε is covered by a finite collection of set {H1,…,Hk}, Sp is covered by the finite collection {H1,…,Hk,Hβ}. Since Sβ=S1. Henceforth, we will say a closed and bounded set is compact. As an application of the Heine-Borel theorem, we prove the following theorem of Bolzano andWeierstrass. Bolzano-Weierstrass theorem. Every boumded infinite set of real numbers has at least one limit point. Proof: We will show that a bounded nonempty set without a limit point can contain only a finite number of points. If S has no limitpoints,then S is closed and every point x of S has an open neighborhood Nx that contains no point of other than x. The collection H={Nx| x
Taylor’s formula. Answer: A polynomial is of the form P(x)=Q0+Q1(x-x0)+…+an(x-x0)n (1) where Q0,Q1,…Qn and x0 are constants. In particular, a constant polynomial P(x)=Q0 is of degree zero, if Q0 If f is differentiable all x0, then f(x)=f(x0)+f’(x0)(x-x0)+ Where The polynomial T1(x)=f(x0)+f’(x0)(x-x0) which is of degree
Now suppose that f has n derivatives at x0 and Tn is the polynomial of degree Tn(r)(x0)=f(r)(x0) 0 Tn is polynomial of degree Tn(x)=a0+a1(x-x0)+…+an(x-x0)n (4) Differentiating (4) yields Tn(r)(x0)=r!ar So (3) determines ar uniquely as ar=f(r)(x0)/r! Therefore, Tn(x)=f(x0)+ We callTn the n-th Taylor polynomial of f about x0 (xxx дегенимиз x3) 1. sinx=x – 2. cosx=1 – – 3. ln(1+x)=x – x2/2 + x3/3 – x4/4 + x5/5 - … 4. ex= 1+ x + x2/2! +x3/3! + x4/4! + … 5. (1+x)a=1 + ax + a(a-1)x2/2! + a(a-1)(a-2)x3/3! + … + xa The real numbers. Supremum and Infimum of a set. Answer: The real number system is first of all a set {a,b,c,…} on which the operation of addition and multiplication a defined that every pair of real numbers has a unique sum and product, both real numbers,with the following properties, A) a+b=b+a and ab=ba (commutative laws) B) (a+b)+c=a+(b+c) (ab)c=a(bc) (associative laws) C) a(b+c)=ab+ac (distributive law) D) There are distinct real numbers 0 and 1 such that a+0=a and a1=a for all a E) For each (a) there is a real number –a such that a+(-a)=0 and if a A set on which two operations are difined so as to have properties (A)-(E) called a field. The simplest possible field consist of two elements which we denote by 0 and 1, with addition defined by 0+0=1+(-1)=0, 1+0=0+1=1 (1) and multiplication defined by 0×0=0×1=1×0=0, 1×1=1 (2) The order Relation The real number system is ordered by relation <, which has the following properties: F) For each pair of real numbers (a) and (b) exactly one of the following is true: a=b,a<b or a>b G) If a<b and b<c, then a<c (The relation < is transitive) H) If a<b,thena+c<b+c for any c and if c>0, then a×c<b×c. A field with an order relation satisfying (F)-(H) in an ordered field. Theorem 1 (The Triangle Inequality). If a and b are any two real numbers then: |a+b|≤|a|+|b| (3) Corollary 2. If a and b are any two real numbers then |a-b|≥||a|-|b|| (4) and |a+b|≥||a|+|b|| (5) supremum of a set: A set S of real numbers is bounded above if there is a real number b such that x≤b whenever x If Example: If S is the set of negative numbers, then any nonnegative number is an upper bound of S,and sup=0 1.2 If S1 is the set of negative integers,then any number a such that a≥-1 is an upper bound of S1, sup=-1 This example shows that a supremumof a set may or may not be in the set, since S1, contains its supremum, but S does not. A nonempty set is a set that has at least one number. The empty set, denoted by The Completeness Axiom. (I) If a nonempty set of reak numbers is bounded above, then it has a supremum. Property (I) is called conpleteness and we say that the real number system is a complete ordered field. Thorem 3. If a nonempty set S of real numbers is bounded above, then sups is the unique real number β such that (a) x≤β for all x in S. (b) if ε>0 there is an x0 in S such that x0>β-ε Proof: we first show that β=supS has properties (a) and (b). Since β is an upper bound of it must satisfy (a). Since any real number a less than β can be written as β-ε with ε=β-a>0, (b) is just another way of saying that no number less than β is an upper bound of S, β=supS (satisfies (a) and (b)) Now we show that, there cannot be more than one real number with properties (a) and (b). Suppose thatβ1<β2 and β2 has property (b) thus, if ε>0, there is an x0 in S such that x0> So β1 cannot have property (a). Therefore, there cannot be more than one real number that satisfies both (a) and (b). Some Natation: “x is a member of S”=>x Theorem 4. (The ArchemedeanProperty). If p and ε are positive, then nε>p for some integer n. Proof: The proof is by contradiction. If the statement is false, p is an upper bound of the set S={| x | x = nε, n is a integer}. Therefore, S has a supremum β, by property (I). Therefore, nε≤β (b) 1.3 For all integer whenever n is, (b) implies that (n+1)ε≤β and therefore nε≤β-ε for all integers n. Hence, β-ε is an upper bound of S. Since, β-ε<β, this contradicts the definition of β. Infimum of a set. A set S of real numbers is bounded below if there is a real number a such that x≥a, whenever x
Theorem 8. If nonempty set S of real numbers is bounded below, then infS is the unique real number α such that: (a) x≥α for all x in S. (b) If ε>0, there is an x0 in such that x0< α+ε Proof: A set S in bounded, of there are numbers a and b such that a≤x≤b for all x in S. A bounded nonempty set has a unique supremum and a unique infimum, and: infS≤supS. A nonempty set S of real numbers is unbounded above if it no upper bound, or unbounded below, if it has no lower bound - We call to indicate that S is unbounded above, and infS=- to indicate that S is unbounded below. (a) If a is any real number, then: a+ (b) If a>0, then: a (c) If a<0, then: a We also define: Finally, we define |
Some set theory. Answer: Definition: Let S and T be set: a) S contains T, and we write S c T or T c S, if every number of T is also in S. in this case, T is a subset of S. b) S\T is the set of elements that are in S, but not in T. c) S equals T, and we write: S=T, is S contains T, and T contains S, thus, S=T if and only if S and T have the same members. d) The compecment of S denoted by Sc, is the set of elements in the universal set that are not in S. e) The union of S and T, denoted by S f) The intersection of Sand T, denoted by S Definition If x0 is real number and, ε>0, then the open interval (x0-ε,x0+ε) in an neighborhood of x0. If the set S contains an ε-neighborhood of x0, then S is a neighborhood of x0, and x0 is an interior point of S. Definition. Let S be subset of R. Then (a) x0 is a limit-point of S, if every deleted neighborhood of x0 contains a point of S. (b) x0 is boundary point of S, if every neighborhood of x0 contains a least one point in S and one not in S. The set of boundary points of S denoted by The closure of S, denoted by (c)x0 is exterior to S, of x0 is in the interior of Sc Theorem. A set Sis closed, if and only if no point of Scis a limit point of S. Corollary. A set is closed, if and only if it contains all its limit points. Definition. A collection H of open sets, is an open covering of a set S, if every point in S is contained in a set H belonging to H, that is, if Sc
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 550; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 T, is the set of elements in at least one of S and T.
T, is the set of elements in at least one of S and T. T is the set of element in both S and T. If S
T is the set of element in both S and T. If S  0(the empty set), then S and T are disjoint sets.
0(the empty set), then S and T are disjoint sets. S
S =S
=S 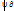 S
S {H|HcH}
{H|HcH} [α;t] for
[α;t] for  ≥α.
≥α. F. To do this, we use the completeness of the reals.
F. To do this, we use the completeness of the reals. S. Then, since S is closed λ is not a limitpointof S. Consequently, there is an ε>0 such that [λ-ε, λ+ε]
S. Then, since S is closed λ is not a limitpointof S. Consequently, there is an ε>0 such that [λ-ε, λ+ε]  , so Sλ-ε=Sλ+ε
, so Sλ-ε=Sλ+ε 0
0 (x-x0)
(x-x0) =0
=0 1 and satisfies T1(x)=f(x0) T’1(x0)=f’(x0), approximates f so well near x0 that
1 and satisfies T1(x)=f(x0) T’1(x0)=f’(x0), approximates f so well near x0 that =0 (2)
=0 (2) (x-x0) +
(x-x0) +  (x-x0)2 + …+
(x-x0)2 + …+  (x-x0)n =
(x-x0)n =  (x-x0)r
(x-x0)r +–
+–  -–
-–  +….
+…. + –
+ –  – –
– –  + –
+ –  - …
- … such that a
such that a  is an upper bound of S, but no number less than β is, then β is a supremum of S and we write β=supS
is an upper bound of S, but no number less than β is, then β is a supremum of S and we write β=supS , is the set that has no numbers.
, is the set that has no numbers. 2-ε. Then by taking ε=β2-β1, we see that there is an x0 in S such that x0>β2-(β2-β1)=β1,
2-ε. Then by taking ε=β2-β1, we see that there is an x0 in S such that x0>β2-(β2-β1)=β1,
 but no number greater than α is, then α is an infimum of S, and we write: α=infS.
but no number greater than α is, then α is an infimum of S, and we write: α=infS. < x <+
< x <+  points of infinity. If (S)is a nonempty set of real numbers, we write: supS=
points of infinity. If (S)is a nonempty set of real numbers, we write: supS=  (8)
(8) =
=  =0
=0 =(-
=(- 


