
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
L’Hospital’srule.The other indeterminate form.Содержание книги
Поиск на нашем сайте
Answer: Theorem. Suppose that f and g are differentiable and g’ has no zeros on (a;b)
And suppose that Proof: Suppose,that ε>0. From (3), there is x0 Cauch’s Theorem implies that if x and t are in [x0,b), then for every c between them, and therefore in (x0,b), such that (g(x)-g(t))f’(c)=(f(x)-f(t)g’(c)) (6) Since g’ has no zeros in (a,b) Lagranzh’s Theorem implies that g(x)-g(t) This means that g cannot have more than one zero in (a,b). Therefore, we can choose x0 so that, in addition to (5), g has zero in [x0,b) Then (6) can be rewritten as so implies that as | If (1) holds, Let x be fixed in [x0,b), and consider the function 10.2 G(t)= From (1) So Since, І G(t) І<ε if t L’Hospital’s rule используется: (0/0) and (&/&).The other indeterminate form:0&, &-&, 00,1&,&0. Ары каратай далелдеу керек еще!!!!» a) The indeterminate form 0 Similar statements apply to limits as x->b+, x->b, x-> b)The indeterminate form
In this case reduced to a common dehominator. c)The indeterminate form 00,1&, Taylor’s formula. Answer: A polynomial is of the form P(x)=Q0+Q1(x-x0)+…+an(x-x0)n (1) where Q0,Q1,…Qn and x0 are constants. In particular, a constant polynomial P(x)=Q0 is of degree zero, if Q0 If f is differentiable all x0, then f(x)=f(x0)+f’(x0)(x-x0)+ Where The polynomial T1(x)=f(x0)+f’(x0)(x-x0) which is of degree
Now suppose that f has n derivatives at x0 and Tn is the polynomial of degree Tn(r)(x0)=f(r)(x0) 0 Tn is polynomial of degree Tn(x)=a0+a1(x-x0)+…+an(x-x0)n (4) Differentiating (4) yields Tn(r)(x0)=r!ar So (3) determines ar uniquely as ar=f(r)(x0)/r! Therefore, Tn(x)=f(x0)+ We callTn the n-th Taylor polynomial of f about x0 (xxx дегенимиз x3) 1. sinx=x – 2. cosx=1 – – 3. ln(1+x)=x – x2/2 + x3/3 – x4/4 + x5/5 - … 4. ex= 1+ x + x2/2! +x3/3! + x4/4! + … 5. (1+x)a=1 + ax + a(a-1)x2/2! + a(a-1)(a-2)x3/3! + … + xa Analysis of function using the derivative plotting graph of function. Answer: To construct the graph of the function y=f(x) to find: 1. Domain and Range 2. Symmetries f is said to be an even function (if f(-x)=f(x)), and is said to be an odd function (if f(-x)=-f(x)) 3. Points of discontinuity. The line x=a is called a vertical asymptote of the curve y=f(x), if 4. Asymptotes (oblique or slant) Y=kx + b, k= 5. X-intercepts (zeros of function and the region of constant sign) 6. Relative extrema (max and min). If f’(x)>0, for every value ox x in (a;b), then f is increasing on [a;b]. If f’(x)<0, for every value ox x in (a;b), then f is decreasing on [a;b]. If f has a relative extremum at x=x0 is a critical point of f; that is, either f’(x0)=0 or f is not differentiable at x0. 7. Concavity, inflection points. a) If f’’(x)>0, for every value of x, then f is concave up on that interval.
b) If f’’(x)<0, for every x in the open interval, then f is concave down on that interval. If a function f changes the direction of its concavity at the point (x0,f(x0)), then we say that f has an inflection point at x0
13. Integration. Indefinite integral. Answer: Definition. A function f is called an Antiderivative of a function f on the given open interval, if F’(x)=f(x) for all x in the interval. For example, the function F(x)= However, F(x)= Since, ( If F(x) is any antiderivative of f(x), then F(x) + C is also an antiderivative on that interval. The process of finding antiderivative is called integration.
The expression Equation (1) should be real as: “The integral of f(x) with respect to x is equal to F(x) plus a constant. ” Integration formulas: 1) 2) 3) 4) 5) 6) 7) 8)
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.44 (0.009 с.) |

 (x)=
(x)=  (x)=0 (1) or
(x)=0 (1) or (2)
(2) =L (3) Then
=L (3) Then  =L (4)
=L (4) (a;b) such that |
(a;b) such that |  – L |<ε if x0<c<b(5)
– L |<ε if x0<c<b(5) 0 if x,t
0 if x,t  =
=  (t)=
(t)=  (t)=0
(t)=0 (t)=
(t)=  -L (8)
-L (8) ε.This holds for all x in (x0,b), which implies (4)
ε.This holds for all x in (x0,b), which implies (4) : we say that a product fg is of the form 0
: we say that a product fg is of the form 0 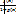 =(
=( ), f(x)g(x)=
), f(x)g(x)=  (since one of the rations is the form (
(since one of the rations is the form ( ))
)) : A difference (f-g) is of the form (
: A difference (f-g) is of the form ( (x)=
(x)=  (x)=
(x)=  (x-x0)
(x-x0) =0
=0 =0 (2)
=0 (2) (x-x0) +
(x-x0) +  (x-x0)2 + …+
(x-x0)2 + …+  (x-x0)n =
(x-x0)n =  (x-x0)r
(x-x0)r +–
+–  -–
-–  +….
+…. + –
+ –  – –
– –  + –
+ –  - …
- …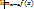 =
=  , b=
, b=  if k=0, then y=b is a horizontal asymptote.
if k=0, then y=b is a horizontal asymptote. x4 is an antiderivative of f(x)=x3 on the interval (-
x4 is an antiderivative of f(x)=x3 on the interval (-  = F(x) + C.
= F(x) + C. 3 dx = x4/4 + C.
3 dx = x4/4 + C. =x + C; 9)
=x + C; 9)  =arcsin
=arcsin  + C;
+ C;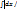 a2 +x2=
a2 +x2=  arctg
arctg  =sinx + C; 11)
=sinx + C; 11)  =ln|x +
=ln|x +  | + C;
| + C; =-cosx + C; 12)
=-cosx + C; 12)  ln|
ln|  + C;
+ C;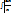 = ln|x| + C;
= ln|x| + C; =
=  + a2/2arcsin
+ a2/2arcsin  xdx = ex + C; 15)
xdx = ex + C; 15)  =
=  + a2/2ln|x +
+ a2/2ln|x +  xdx = ax/lna + C;
xdx = ax/lna + C;


