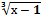Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки наибольшего и наименьшего носятСодержание книги Поиск на нашем сайте
А)глобальный характер В)локальный характер С)просто равны 0 Формула т.Лагранжа А) f´(ζ)= В) f´(ζ)= С) f´(ζ)= 17.рынок свободной конкуренции характеризуется: А)полным контролем цен В)отсутствием контроля цен С)равновесными ценами 18.в чем основная задача дифференциального исчисления: А) нахождение производной данной функции В)нахождении дифференциала С)нахождение первообразной 19.касательной к кривой в точке, называют: А)прямую, пересекающую график в 1 точке В)предельное положение касательной С)предельное положение секущей, приΔΧ→O Функция гладкая А)нет точек разрыва В)одна точка разрыва С)имеет производную на этом промежутке. Тест завершен
Дата заполнения «______» июня 2011г.
Тестовое задание По предмету: «математика для экономистов» ВАРИАНТ №_3_ Ф.И.___________________________________ Алгебраическая сумма конечного числа бесконечно малых величин, есть А.нуль В.постоянная величина С.бесконечно малая величина Д.бесконечно большая величина Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть А.нуль В.постоянная величина С.бесконечно малая величина Д.бесконечно большая величина 3.найдите верное высказывание: А.бесконечно большая величина есть ограниченная функция В.неограниченная функция не обязательно бесконечно большая С.неограниченная функция обязательно бесконечно большая Д.ограниченная функция есть бесконечно малая Две бесконечно малые величины эквивалентны, если А. предел их отношения равен 0 В. предел их отношения равен1 С. предел их отношения равен∞ Д. предел их отношения равен const Точка а называется точкой разрыва первого рода, если А.правый и левый пределы равны В.конечные односторонние пределы не равны друг другу С.предел в этой точке существует но не равен нулю Д.функция не определена в этой точке 6.чему равно приращение функции у=С А.1 В.0 С.самой постоянной Д.∞ Найдите верное высказывание А.если функция непрерывна в точке, то она дифференцируема В.если функция дифференцируема в точке, то она непрерывна С.производная всегда непрерывна Д.нет не непрерывных функций Экономический смысл производной А.угловой коэффициент касательной к графику в точке t0 В. производная пути по времени есть ускорение точки а(t0)=s΄(t0) С. производная пути по времени есть скорость точки v(t0)=s΄(t0) Д.производная объёма произведенной продукции по времени есть производительность труда в момент t0 Физический смысл производной. А.угловой коэффициент касательной к графику в точке t0 В. производная пути по времени есть ускорение точки а(t0)=s΄(t0) С. производная пути по времени есть скорость точки v(t0)=s΄(t0) Д.производная объёма произведенной продукции по времени есть производительность труда в момент t0 Геометрический смысл производной. А.угловой коэффициент касательной к графику в точке t0 В. производная пути по времени есть ускорение точки а(t0)=s΄(t0) С. производная пути по времени есть скорость точки v(t0)=s΄(t0) Д.производная объёма произведенной продукции по времени есть производительность труда в момент t0 Геометрический смысл теоремы Ферма: в точке наибольшего(наименьшего)значения, достигаемого внутри интервала А. касательная параллельна Ох В. касательная параллельна Оу С.перпендикулярна биссектрисе угла Д.совпадает с одной из осей Если производная дифференцируемой функции положительна внутри промежутка А.функция возрастает В.функция убывает С.функция постоянна Д.функция возрастает на этом промежутке Если производная дифференцируемой функции отрицательна внутри промежутка А.функция возрастает В.функция убывает на этом промежутке С.функция постоянна Д.функция возрастает на этом промежутке 14.найти критические точки функции у= А.х=0 В.х=1 С.х=-1 Д.нет кр. точек Если вторая производная дважды дифференцируемой функции положительна внутри некоторого промежутка, то А.функция постоянна на промежутке В.функция имеет точку перегиба С.функция выпукла вверх Д.функция выпукла вниз
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |


 ,функция дифференцируема
,функция дифференцируема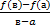 ,функция непрерывна, дифференцируема
,функция непрерывна, дифференцируема