
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенство Коши-БуняковскогоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим неравенство Коши в пространстве Rn. Для начала дадим определение n–мерного евклидового пространства Rn n–мерное точечное пространство, в котором расстояние между точками определено по данной формуле
называется n–мерным евклидовым пространством и обозначается Rn. Ясно, что при всех i = 1, 2,.,n. Также ясно, что
Это неравенство в двумерном или трехмерном пространстве выражает тот элементарный геометрический факт, что сумма двух сторон треугольника не меньше третьей стороны, и потому называется неравенством треугольника. Также данное неравенство является одним из аксиом метрического пространства и называется аксиомой треугольника Предварительно установим важное неравенство Коши
справедливо для любых вещественных чисел ai и bi. Простое доказательство этого неравенства основывается на следующем замечании: если квадратный трехчлен Ax2+2Bx+C с вещественными коэффициентами неотрицателен при всех вещественных x, то его дискриминант Составим вспомогательную функцию
где
Из определения Тогда, на основании предыдущего замечания,
это и есть иначе записанное неравенство Коши. Далее из неравенства (3) выведем еще одно неравенство
(ai и bi – любые вещественные числа), которое тоже называют неравенством Коши. Для доказательства неравенства (4) извлечем квадратные корни из обеих частей неравенства (3), затем удвоив обе части полученного нового неравенства и прибавим к ним выражение . В результате получим
Это неравенство можно переписать и так:
Извлекая, квадратные корни из обеих частей последнего неравенства, получим (4).Теперь уже легко доказать неравенство треугольника (2).
Пусть
Полагая в неравенстве (4)
мы получим неравенство (2).
Теперь приведем некоторые примеры метрических пространств. Пусть множество l состоит из всех бесконечных числовых последовательностей
Таким образом, l – метрическое пространство Обозначим через l2 множества всех таких последовательностей вещественных чисел, для которых
Прежде всего нужно проверить, что
которое мы будем называть неравенством Коши для бесконечных последовательностей. Аналогичным образом из неравенства (3) выводится и другое неравенство Коши для бесконечных последовательностей:
Из неравенства (5), в частности, следует, что если и Теперь проверка выполнения в l2 аксиом метрического пространства может быть произведена совершенно так же, как это сделано для Rn. Пространство l2 иногда называют бесконечномерным евклидовым пространством. Неравенство треугольника. Если x и y –произвольные векторы, то по аналогии с элементарной геометрии вектор x+y естественно называть третьей стороной треугольника, построенного на векторах x и y. Используя неравенство Коши–Буняковского, мы получаем
или
Неравенства (7)–(8) называются неравенствами треугольника. Геометрически они означают, что длина любой стороны всякого треугольника не больше, чем сумма длин двух других сторон, и не меньше, чем абсолютная величина разности длин этих сторон.
Глава 3. Множества связные, несвязные, ограниченные, неограниченные. Множества связные несвязные Понятия относящиеся к множествам точек в Пусть
сопоставляющее каждому Пусть теперь все функции
Определение. В описанной выше ситуации будем называть отображение
заданное формулой
Рис.
Множество всех точек Определение: Множество
Примеры связных областей на плоскости.
Связными областями являются: 1) всё пространство 2) замкнутые и открытые шары; 3) гиперплоскости; 4) замкнутые и открытые полупространства; 5) замкнутые и открытые параллелепипеды; 6) положительный и неотрицательный октанты.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1066; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.13.15 (0.009 с.) |

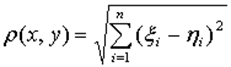 ,
, тогда и только тогда, когда x = y, т. е. когда
тогда и только тогда, когда x = y, т. е. когда 
 .Докажем, что для любых трех точек
.Докажем, что для любых трех точек 
 (2)
(2) , (3)
, (3) *.
*. от вещественной переменной x, сводящуюся к квадратному трехчлену:
от вещественной переменной x, сводящуюся к квадратному трехчлену: ,
,
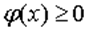 при всех x.
при всех x.
 (4)
(4)

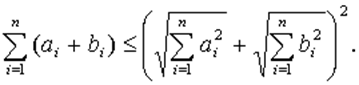


 удовлетворяющих условию
удовлетворяющих условию

 , и положим
, и положим .
. конечно (т. е. что ря в правой части сходится) для любых x и y из l2. А для этого сначала покажем, что неравенство Коши (4) справедливо и для бесконечных последовательностей чисел ai и bi (i=1, 2,.). Действительно, беря произвольное натуральное n, запишем неравенство (4), а затем перейдем в нем к пределу при
конечно (т. е. что ря в правой части сходится) для любых x и y из l2. А для этого сначала покажем, что неравенство Коши (4) справедливо и для бесконечных последовательностей чисел ai и bi (i=1, 2,.). Действительно, беря произвольное натуральное n, запишем неравенство (4), а затем перейдем в нем к пределу при  . Получим неравенство
. Получим неравенство . (6)
. (6)
 , то и последовательность
, то и последовательность  , т.е.
, т.е.  .
.
 (7)
(7) (8)
(8) .
. -- отрезок
-- отрезок  на вещественной оси
на вещественной оси 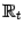 , переменная на которой обозначается буквой
, переменная на которой обозначается буквой  . Рассмотрим
. Рассмотрим  функций
функций , заданных на отрезке
, заданных на отрезке  . Каждому
. Каждому 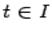 соответствует тогда точка
соответствует тогда точка  пространства
пространства 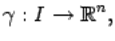
 соответствующую точку
соответствующую точку  . Это отображение
. Это отображение  называется вектор-функцией, заданной на отрезке
называется вектор-функцией, заданной на отрезке  .
. , задающие вектор-функцию
, задающие вектор-функцию  в положение
в положение  .
.
 , непрерывным путём, или просто путём, соединяющим точку
, непрерывным путём, или просто путём, соединяющим точку  с точкой
с точкой  пространства
пространства 
 будем называть непрерывной линией в
будем называть непрерывной линией в  -- параметризацией этой линии. Заметим, что одна и та же линия
-- параметризацией этой линии. Заметим, что одна и та же линия  может иметь разные параметризации. Например, на плоскости
может иметь разные параметризации. Например, на плоскости  с координатами
с координатами  отрезок
отрезок  оси
оси  можно параметризовать, положив либо
можно параметризовать, положив либо  , либо
, либо  (разумеется, формулы
(разумеется, формулы  , при любом
, при любом 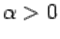 задают ещё бесконечное множество различных параметризации той же линии
задают ещё бесконечное множество различных параметризации той же линии  называется связным, если любые две точки
называется связным, если любые две точки  этого множества
этого множества  можно соединить непрерывной линией
можно соединить непрерывной линией  и заканчивающийся в
и заканчивающийся в  при всех
при всех  .
.



