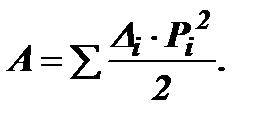Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение усилий в стержнях ферм способом сечений.Содержание книги
Поиск на нашем сайте
Расчет выполняется в последовательности: – определяются опорные реакции, если они ранее не были определены; – ферма разрезается на две части сечением, которое проходит через стержни, усилия в которых необходимо определить; при этом должно разрезаться не более трех стержней, усилие в которых неизвестны; – рассматривается равновесие одной из двух частей фермы; действие отброшенной части заменяется реакциями перерезанных стержней, которые направляются вдоль стержней от узлов; изображаются активные силы, действующие на рассматриваемую часть фермы; – составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие. Обычно составляются уравнения моментов сил относительно точек, где пересекаются линии действия двух неизвестных усилий. Если же на расчетной схеме два стержня параллельны, то составляется уравнение проекций сил на ось, перпендикулярную к этим стержням; – решая каждое из составленных уравнений равновесия, находят искомые усилия в стержнях.
Д3 -? ∑Мкпр =0 Д3*r- P(l1 + d1)+ R b *l1 = 0
29. Построение линий влияния усилий в стержнях ферм. Рассмотрим ферму (рис. 5.6 а). При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки (рис. 5.6 б). Поэтому ЛВ опорных реакций фермы будут аналогичны ЛВ балки (рис. 5.6 в, г). Для построения ЛВ продольных усилий фермы воспользуемся способами вырезания узлов и сквозных сечений. а) Использование способа вырезания узлов Для построения ЛВ N2-6 вначале рассмотрим узел 1. Так как к этому узлу силы не приложены, то по признаку 1 N1-6=0. После этого вырежем узел 6 фермы. Здесь могут быть два случая: 1) когда единичная сила P=1 находится в этом узле (рис. 5.6 е), то SY= N2-6 sina+1–1=0. Отсюда N2-6=0. 2) когда единичная сила P=1 находится вне этого узла (рис. 5.6 ж), то SY=N2-6 sina+RA=0. Отсюда N2-6= – Тогда, используя ЛВ опорной реакции RA, можно построить ЛВ усилия N2-6 (рис. 5.6 д).
Рис. 5.6 б) Использование способа сквозных сечений Поперек фермы проведем сквозное сечение I–I (рис. 5.7 а) и получим независимые левые и правые части. Единичная сила P=1 может находиться в обоих частях фермы. 1)Единичная сила левее сечения(рис. 5.7 б): SM SY 2)Единичная сила правее сечения (рис. 5.7 в): SM SY В первом случае определяем ординаты ЛВ этих усилий между узлами 6-7, т.е. определяем их левые ветви, а во втором случае определяем ординаты обоих ЛВ между узлами 8-10, т.е. определяем правые ветви ЛВ. Соединив точки между узлами 7-8, получаем переходную прямую и окончательный вид ЛВ (рис. 5.7 г, д).
Рис. 5.7 Как видно из этих примеров, у ЛВ продольных усилий фермы есть следующее свойства: ветви ЛВ пересекаются под моментной точкой; если же моментной точки нет, ветви ЛВ параллельны. 30 Расчет комбинированных систем. Называется системы состоящие из 2 частей жесткой и гибкой.
В гибкой только продольные силы.
∑Мспр =0 -Rb(l1 + (l2)/2) + N3 *h = 0 à N3
∑X =0 N3 – N1 cosα = 0 à N1 ∑Y =0 N1 sinα + N2 = 0 à N2
Далее решаем балку
31) Работа статически приложенных внешних сил. Примем, что на конструкцию действует статическая внешняя нагрузка, т.е. нагрузка, которая возрастает от нуля до своего предельного значения с такой скоростью, что возникающими инерционными силами можно пренебречь. При малых деформациях, когда напряжения не превышают предела пропорциональности, применим принцип независимости действия сил. Определим работу статической внешней нагрузки (P или m) приложенной к упругой системе, материал которой удовлетворяет закону Гука. Перемещение некоторой точки от силы Р (рис. 8.1) будет:
где a – коэффициент пропорциональности, его величина зависит геометрии сооружения, вида сечения и материала.
Поворот некоторого сечения от сосредоточенного момента m будет
В дальнейшем все рассуждения проведем на примере действия сосредоточенной силы Р и обобщим на другие случаи нагружения. Увеличим силу Р на dP, что вызовет приращение перемещения dD. Найдем величину элементарной работы внешней силы на перемещении dD:
Найдем выражение для определения работы при изменении внешней силы от нуля до конечной величины:
так как aР = D, то
Мы получили теорему Клапейрона: Работа внешней силы при статическом ее приложении на сооружение равна половине произведения ее значения на величину соответствующего ей перемещения. Легко обобщить полученный результат на случай, когда к сооружению приложена система статических внешних сил:
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 895; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.006 с.) |


 ×RA.
×RA.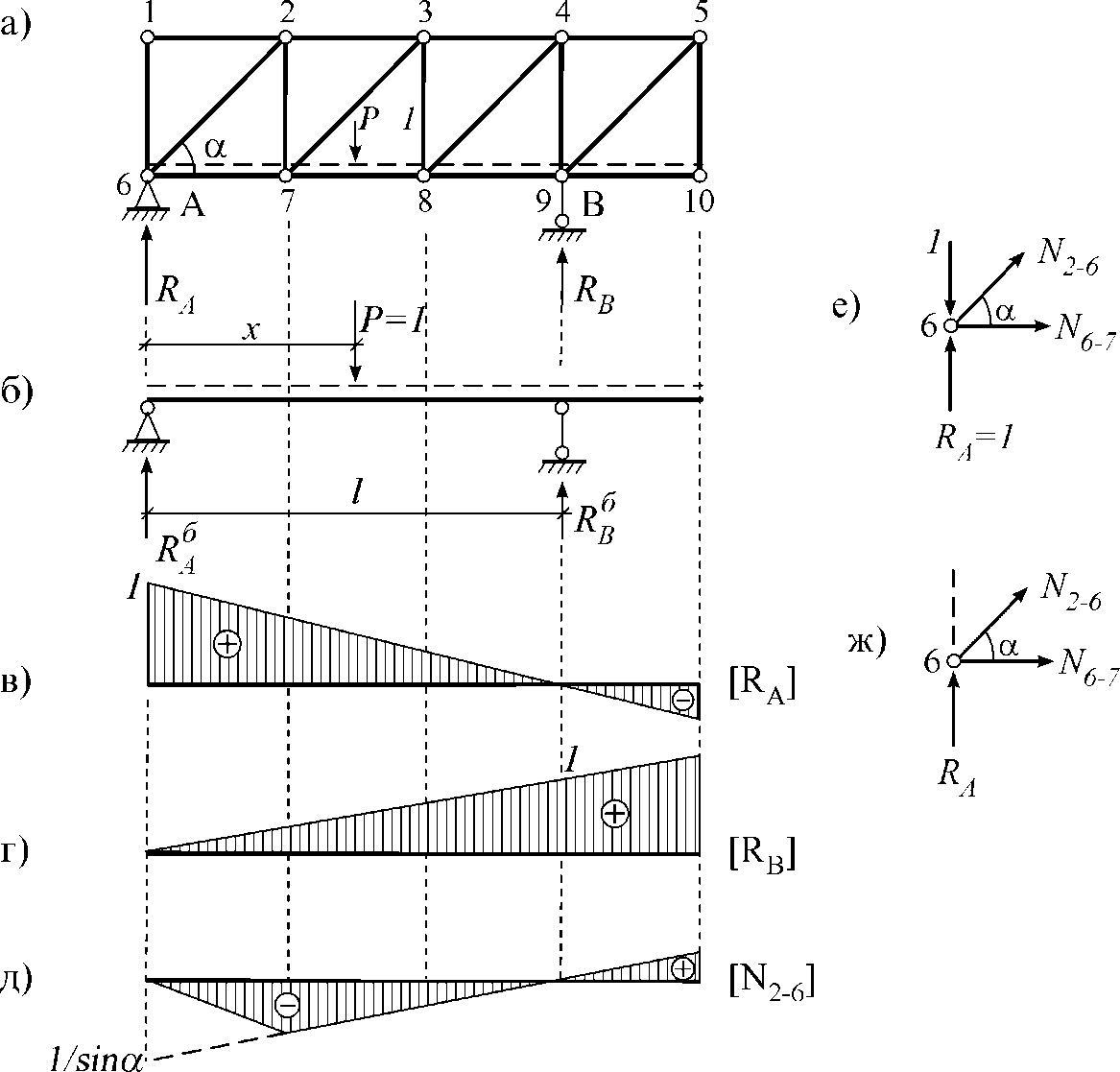
 =N2-3 h+RB 2a=0. Отсюда N2-3= –2
=N2-3 h+RB 2a=0. Отсюда N2-3= –2  RB ;
RB ; = –N3-7 sin a +RB=0. Отсюда N3-7=
= –N3-7 sin a +RB=0. Отсюда N3-7=  RB .
RB . = –N2-3 h – RA a=0. Отсюда N2-3= –
= –N2-3 h – RA a=0. Отсюда N2-3= –  =N3-7 sina+RA=0. Отсюда N3-7= –
=N3-7 sina+RA=0. Отсюда N3-7= – 

 Расчет начинается с определения определения опорных реакций. Определения продельных усилий.
Расчет начинается с определения определения опорных реакций. Определения продельных усилий.
 ,
,
 .
. × dD
× dD ,
,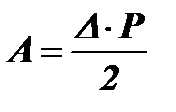 .
.