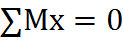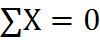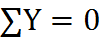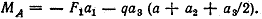И 4. Клас-ия опор соор-ий. Реакции опор и клас-ия нагрузок на соор-ия

Всякое соор-ие соед-ся с основанием с пом-ю опорных связей. Опорные связи могут в основном быть трех видов:

- шарнирно-подв-ая опора:

- шарнирно-неподв-ая опора:

- жесткая заделка:

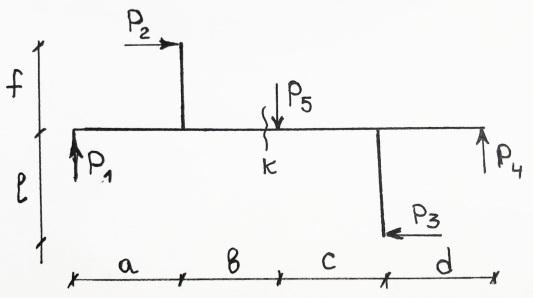
Внутр-ие усилия, возник-ие в элементах стр-ых констр-ий

Под дей-ем вн-их нагрузок в элементах всякого соор-ия могут возникать изгиб-ие моменты, попер-ые силы и продольные силы.

Изгиб-им моментом в каком-либо сеч-ии соор-ия наз-ся внутр-яя пара сил, численно равная сумме моментов всех вн-их сил, вкл-ая опорные реакции, располож-ых с одной стороны от сечения, относ-но от центра тяж-ти данного сеч-ия.

При опред-ии внутр-их усилий дял наглядности строят эпюры этих усилий.

Эпюра – это график, показ-щий усилия по всем элементам соор-ия.

На эпюре изгиб-их моментов знаки не ставят, а ординаты эпюры отклад-ся со стороны растянутых волокон стержня.

Попер-ые или прорезающие силы в сеч-ии наз-ся сумма проекций всех вн-их сил, располож-ых с одной стороны от сеч-ия на перпендикуляр к оси стержня данного сеч-ия.

Попер-ая сила счит-ся полож-ой, если она вращает вокруг сеч-ия по часовой стрелке.

Продольной силой в сеч-ии наз-ся сумма проекций всех вн-их сил, располож-ых с одной стороны от сеч-ия на касат-ую к оси стержня данного сеч-ия.

Растягивающая продольная сила счит-ся полож-ой, сжимающая – отриц-ой.

Для опред-ия внутр-их усилий исп-ся способ сеч-ий, согласно к-му сеч-ем, в к-ом опред-ся усилие, констр-ия рассекается на две части и рассм-ся равновесие любой из них.

Сущность метода сечений.

Для определения внутр.усилий используется метод сечений, согласно к/т усилие определяется сечением(конструкция рассекается на 2 части и рассматривается равновесие любой из них т.е. одну часть отбрасываем, а другую рассматриваем)

Левая часть: М_к = Р₁(а+b) + P₂f

Правая часть: М_к = P₅*0 + Р₄(с+d) + P₃*l

Поперечная сила:

Qк^лев = Р₁; N_k= -P₂

Qк^прав = Р₅ - Р_4; N_k= -P₃

На участках,где отсутствует распределенная нагрузка эпюра моментов прямолинейна. На уч-ках, где присутствует распред. нагрузка эпюра криволинейна. В сечениях где приложена сосредоточенная сила,на эп.М есть излом. В сеч-ях, где приложен сосредот.момент,на эп.М должен быть скачок на величину этого момента.Для эп.Q на уч-ках,где отсутствует распред.нагрузка эп.Q прямолинейна и II оси.На уч-ках с равномерно распред. нагрузкой эп.Q прямолинейна и наклонена к оси.В сеч-ях,где приложена сосред. сила на эп.Q скачок на величину этой силы.В той точке где эп.Q=0 на эп.М должен быть экстремум.

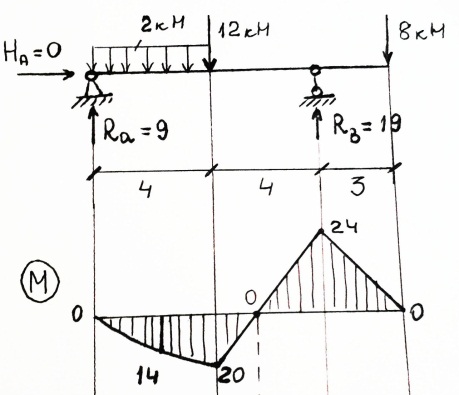
Изгибающий момент в сечении сооружения,как он определяется?

Изгибающим моментом в к/л сечении сооружения наз. внутр.пара сил,численно равная сумме моментов всех внешних сил,включая опорные реакции,расположенные с одной стороны отсечения,отн-но центра тяжести данного сеч-ния. На эпюре изгибающих моментов знаки не ставят,а ординаты эпюры откладывают со стороны растягивающих волокон стержня.

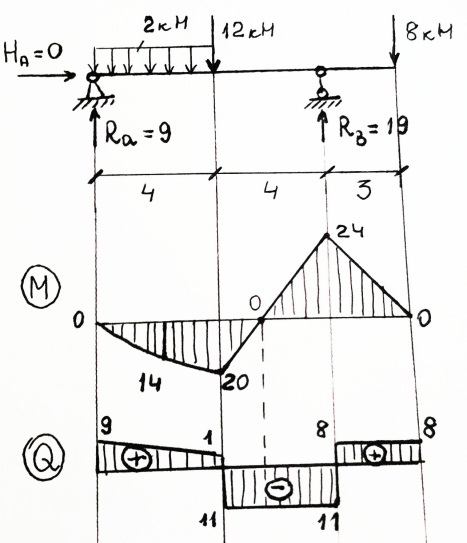
М_а=0; М₁=9*4 - 2*4*4=20кН;

М₂=9*2 - 2*2*1=14кН;

Поперечная сила,ее знаки?

Поперечной или перерезывающей силой наз. сумма проекций всех внешн.сил, расположенных с одной стороны отсечения,на перпендикуляр к оси стержня в данном сеч-нии. Поперечная сила считается положительной,если она вращает вокруг сечения по часовой стрелке, отрицательной -против часовой.

Продольная сила,ее знаки?

Продольная сила в сеч-нии наз. сумма проекций всех внешних сил, расположенных с одной стороны отсечения,на касательную к оси стержня данного сеч-ния. Растягивающая продольная сила считается положительной,сжимающая- отрицательной.

Эпюра внутреннего усилия?

При определении внутр.усилий для наглядности строят эпюры внутренних усилий.

Эпюра – это график,показывающий закон изменения внутр. усилия по длине стержня.

11. Сте́пени свобо́ды - характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.

Определение степеней свободы:

W=3Д – 2Ш – С₀

W=2У – С – С₀ - для ферм

W – число степеней свободы

Д – число жёстких дисков

Ш – число простых цилиндрических шарниров

С₀ – число опорных связей

С – число стержней фермы

У – число узлов фермы

Если

1) W>0 конструкция геометрически изменяема

2) W<0 конструкция статически неопределима

3) W=0 конструкция статически определима

12. Кинемат-ий анализ состоит из 2-ух частей:

А) формальный анализ

Б) структурный анализ

При формальном анализе определяется число степеней свободы системы (см. 11вопр.)

Если

1) W>0 конструкция геометрически изменяема

2) W<0 конструкция статически неопределима

3) W=0 конструкция статически определима

Для установления изменяема или неизменяема конструкция 2 и 3 необходимо провести дополнительный структурный анализ, т.е. установить по каким правилам соединены отдельные диски между собой.

13. Существует 3-и признака образования неизменяемости системы:

1) 3-и деска соединены между собой 3-мя шарнирами не лежащими на одной прямой

2) 2-а диска соединены между собой 3-мя стержнями не параллельными и не пересекающимися в одной плоскости

3) 3-и диска соединены попарно между собой 6-ю стержнями точки пересечения которых не лежат на одной прямой

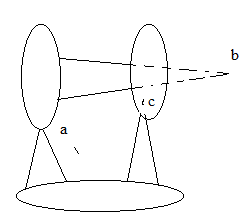
14. Опорные реакции статически определимой системы(балки или ломаного стержня) определяются из уравнений равновесия статики:

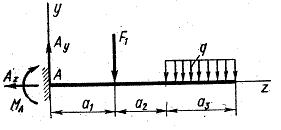
Пример

Решение. Реакцию заделки представляем в виде двух сил Az и Ay, направленных, как указано на чертеже, и реактивного момента MA.

Составляем уравнение равновесия балки.

1. Приравняем нулю сумму проекций на ось z всех сил, действующих на балку. Получаем Az = 0. При отсутствии горизонтальной нагрузки горизонтальная составляющая реакции равна нулю.

2. То же, на ось y: сумма сил равна нулю. Равномерно распределенную нагрузку q заменяем равнодействующей qaз, приложенной посредине участка aз:
Ay - F1 - qaз = 0,
откуда
Ay = F1 + qaз.

Вертикальная составляющая реакции в консольной балке равна сумме сил, приложенных к балке.

3. Составляем третье уравнение равновесия. Приравняем нулю сумму моментов всех сил относительно какой-нибудь точки, например относительно точки А:

откуда

15. Для определения внутренних усилий используют способ сечений. Согласно которому сечением рассекается балка(стержень) на 2-е части и рассматривается равновесие любой из них.

При определении внутренних усилий для нагляднос-ти строятся эпюры этих усилий. Эпюра – это график показывающий распределение данного усилия по всем элементам сооружения.

На эпюре изгибающих моментов знаки не ставятся, а ординаты эпюры ставят со стороны растянутых волокн.

Поперечная или перерезывающая силы в сечении назыв. сумма проекций всех внешних сил расположенных с одной стороны от сечения на перпендик. к оси стержня в данном сечении.

Поперечная сила считается положительной, если она вращает вокруг сечения по часовой стрелке.

Продольной силой называют сумма проекций всех внешних сил расположенных с одной стороны от сечения на касательную к оси стержня в данном сечении.

Растягивающая продольная сила считается полож-ой.

Берёте рисуете любой ломаный стержень и строите эпюры M Q N

 

16. Расчёт балки на неподвижную нагрузку начинается с построения поэтажной схемы, затем рассчитывается самая верхняя второстепенная балка на приложенные к ней внешние нагрузки. Определяются опорные реакции и строятся эпюры Q и M, а затем рассматривается нижележащая балка на действующую на неё нагрузку и реакции опоры вышележащей балки, взятую с обратным направлением.
17. Расчёт балки на неподвижную нагрузку начинается с построения поэтажной схемы, затем рассчитывается самая верхняя второстепенная балка на приложенные к ней внешние нагрузки. Определяются опорные реакции и строятся эпюры Q и M, а затем рассматривается нижележащая балка на действующую на неё нагрузку и реакции опоры вышележащей балки, взятую с обратным направлением.

18. Линия влияния внутреннего усилия – график, показывающий изменение данного усилия в этом же сечении в зависимости от положения на балке подвижно сосредоточенного груза Р=1.

19. Статический метод заключается в том, что груз Р=1 устанавливается в каком-то месте балки. Положение его в данный момент фиксируется ординатой Х, считая, что груз неподвижен, составляется уравнение равновесия, из которого можно было бы определить искомое усилие. Считая в этом уравнении Х переменной, получают уравнение графика изменения данной величины.