
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки і рекомендаціїСодержание книги Поиск на нашем сайте
При нормуванні математичного опису або структурних схем за базове переміщення зручно вибрати максимальне переміщення, що відпрацьовується по трикутної тахограмі:
де εз = εр = - εг = const – задане прискорення при розгоні і гальмуванні привода при відсутності моменту статичного опору; tро – час розгону привода до швидкості ідеального холостого ходу двигуна ω0 при MсΣ=0. Коефіцієнт підсилення регулятора положення в системі з ЗП необхідно вибирати за принципом підлеглого регулювання і оптимізувати з умов модульного оптимуму або з умови відсутності перерегулювання за положенням. Коефіцієнт підсилення регулятора положення в системах без ЗП необхідно вибирати з умови рівноуповільненого руху привода при гальмуванні:
де kω, kφ – коефіцієнти зворотних зв’язків за швидкістю та положенням; Δφm, ωmax – неузгодженість за положенням і швидкість двигуна в момент початку гальмування. Для лінійного РП ωmax вибирається з умови відпрацьовування всіх можливих переміщень без перерегулювання і дотягування, а коефіцієнт kРП уточнюється при моделюванні з умов відпрацьовування базового переміщення без перерегулювання і без дотягування, тому що рівняння (4.2) складено без урахування інерційності контуру швидкості. При моделюванні нелінійного задавача положення (ЗП) необхідно скористатися структурною схемою, наведеною на рис.4.2.
Рисунок 4.2 - Структурна схема ЗП
При моделюванні нелінійного РП необхідно спрямляти початкову ділянку його статичної характеристики і знижувати вихідну напругу нелінійної ділянки цієї характеристики з урахуванням запізнювання моменту початку гальмування внаслідок інерційності контуру швидкості. Моделювати нелінійний РП можна двома способами. Перший – безпосередньо за допомогою базових блоків Simulink за структурною схемою. Другий варіант полягає в тому, що за рівняннями, що описують роботу нелінійного РП, у середовищі пакета MATLAB можна створити функцію, що реалізує алгоритм його роботи, а потім за допомогою Simulink-блоку MATLAB Fn створити модель регулятора положення і вставити її в модель системи. При моделюванні дискретних датчиків швидкості необхідно скористатися наступними передавальними функціями: – для датчика миттєвого значення
– для датчика середнього значення
При моделюванні цифрових ЗІ і ЗП щоб уникнути автоколивань треба замінити ланки "sign" послідовно з’єднаними пропорційною ланкою з великим коефіцієнтом підсилення і типовою нелінійністю “обмеження координат”.
СИСТЕМИ ЕЛЕКТРОПРИВОДУ З ПРУЖНИМИ ЗВ'ЯЗКАМИ Загальні відомості
В реальних системах електроприводу припущення про те, що зв'язок вала двигуна з механізмом є абсолютно жорстким, іноді не може бути прийнятим. На практиці майже усі зв'язки двигуна з механізмом не є абсолютно жорсткими, і можливість не брати до уваги вплив пружності пов'язана з тим, що власна частота пружних коливань системи двигун – механізм набагато вище тих частот, що є важливими для автоматичної системи керування. Саме тому підвищити швидкодію автоматичних систем у класичному варіанті систем підпорядкованого керування іноді неможливо саме за наявності впливу пружності. Для підвищення швидкодії треба застосовувати додаткові корегуючі зв'язки або доповнювати систему комбінованими задатчиками інтенсивності (Додаток Б). Структурна схема двомасового електромеханічного об'єкту (ДЕМО) наведена на рис. 5.1.
Рисунок 5.1 – Структурна схема двомасової електромеханічної системи в абсолютних одиницях виміру
На схемі прийняті такі позначення: ЕП – ЕРС перетворювача; І – струм двигуна; М – електромагнітний момент двигуна; J1 - момент інерції першої маси (двигуна); J2 – приведений до валу двигуна момент інерції другої маси (механізму); JS = J1 + J2 – сумарний момент інерції привода;
c12 – коефіцієнт жорсткості, який є коефіцієнтом пропорційності між пружним моментом МП = с12 (j1 – j2) та кутом скручування пружного елементу; W12 –частота вільних коливань двомасової пружної системи;
Т12 =1/W12 –стала часу вільних коливань двомасової пружно-в’язкої системи; b12 – коефіцієнт внутрішнього тертя в пружній передачі; М12 – пружно-в'язкий момент, що дорівнює сумі пружного МП та в'язкого МВ моментів; j1 – кут повороту вала двигуна; j2 – приведений до валу двигуна кут повороту вала механізму; МС – момент сил протидії (статичний момент).
Як було зазначено вище, у разі побудови класичної двоконтурної системи підпорядкованого керування швидкості такого об'єкту, неможливо досягти високої швидкодії при відсутності пружних коливань. Тому треба використовувати додаткові корегуючі ланки. У теорії систем автоматичного керування відомими є два способи корекції підпорядкованої системи. Це спосіб заведення на регулятор швидкості зворотного зв'язку за першою похідною від швидкості другої маси, та спосіб заведення зворотного зв'язку за другою похідною від швидкості другої маси. Ці способи можна проілюструвати наступним рисунком.
Рисунок 5.2 - Способи корекції роботи систем керування двомасовим електромеханічним об'єктом
На цьому рисунку КЛ1 та КЛ2 – корегуючі ланки, відповідно для системи з додатковим зворотним зв'язком за першою похідною від швидкості другої маси, та для системи зі зворотним зв'язком за другою похідною від швидкості другої маси. При необхідності досягти астатичних властивостей системи керування двомасовим об'єктом можна доповнювати систему ще одним контуром з інтегральним регулятором швидкості (див. рис. 5.2 – зв'язок, що показаний пунктиром). З метою підвищення швидкодії системи керування при відпрацюванні керуючої дії можна використовувати задавач інтенсивності з комбінованим принципом роботи. У випадку системи з пропорційним регулятором швидкості структурну схему такого задавача можна представити у вигляді рис. 1.3 а. На цьому рисунку аперіодична ланка з постійною часу ТФ – це фільтр на вході системи, який треба встановити додатково для реалізації принципів комбінованого керування. У реальних системах цей фільтр вже є присутнім для компенсації впливу фільтру, який встановлюється в зворотному зв'язку за швидкістю з метою фільтрації пульсацій тахогенератора. Сталу часу ТФ можна брати у діапазоні (2 ¸4)Тm. У разі астатичної системи керування з додатковим контуром та інтегральним регулятором швидкості можна скористатися саме інтегральним регулятором і побудувати комбінований задатчика за його допомогою. Структурна схема комбінованого задатчика для астатичної системи керування наведена в Додатку Б на рис. Б.1, б. На рис. 1.3 ланки з коефіцієнтами k1 та k2 – це компадуючі зв'язки, параметри яких розраховуються згідно методики, наведеної нижче. Єдиною величиною, яка може варіюватися у процесі налагодження такої системи керування, є коефіцієнт підсилення контуру швидкості (іншими словами, можна змінювати тільки сталу інтегрування розімкненого контуру швидкості Тш). При параметричному синтезі системи керування ДЕМО треба взяти до уваги той факт, що постійна часу регулятора швидкості має бути набагато більшою, ніж у системи керування одномасовим об'єктом, тобто ми повинні зменшити швидкодію контуру швидкості. Якщо ми будемо використовувати класичну настройку контуру за модульним оптимумом, тобто візьмемо Тш = 2ТС, то отримаємо велику коливальність такої системи, а може, навіть порушимо її сталість. Завдання
1. Виконати математичний опис об'єкта керування – двомасової електромеханічної системи. 2. Розробити структурну модель об'єкта керування у абсолютних та відносниходиницях. 3. Розробити "базову" структурну модель системи керування двомасовим об'єктом. За базову систему керування взяти систему з пропорційним регулятором швидкості, зі звичайним задавачем інтенсивності та без будь-яких корекцій. 4. Синтезувати регулятор швидкості системи за модульним оптимумом. 5. Отримати перехідні процеси у системі управління при відпрацюванні керуючої дії та наявності навантаження. 6. Доповнити базову структурну схему системи керування корегуючим зв'язком, який вказаний у вашому варіанті завдання (табл.5.1). 7. Синтезувати сталу часу регулятора швидкості та коефіцієнт корегуючої ланки за модульним оптимумом. 8. Отримати відповідні перехідні процеси у скорегованій системі керування. 9. Для варіантів з І-РШ доповнити систему ще одним контуром швидкості другої маси з інтегруючим регулятором швидкості та отримати перехідні процеси. 10. Замінити задавач інтенсивності на такий, що реалізує принцип комбінованого керування (якщо це вказано у вашому варіанті), розрахувати його коефіцієнти і отримати перехідні процеси у системі керування при відпрацюванні задаючої дії. 11. Провести дослідження, що вказані у завданні (табл.5.1). Таблиця 5.1 – Варіанти завдань
Таблиця 5.2 – Параметри двомасової електромеханічної системи
Методичні рекомендації
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 (4.1)
(4.1) (4.2)
(4.2)
 (4.3)
(4.3) (4.4)
(4.4)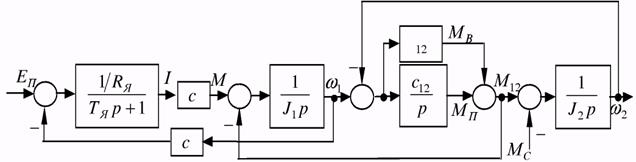
 – коефіцієнт розподілення мас, що показує співвідношення сумарного моменту інерції двигуна і механізму до моменту інерції двигуна;
– коефіцієнт розподілення мас, що показує співвідношення сумарного моменту інерції двигуна і механізму до моменту інерції двигуна; – стала часу вільних коливань двомасової пружної системи;
– стала часу вільних коливань двомасової пружної системи; – стала часу коливань другої маси;
– стала часу коливань другої маси;



