
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные способы получения рациональной основной системы метода сил: выбор симметричной основной системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель- уменьшение трудоемкостей расчетов. Критерием рациональности основной системы явл-ся равенство нулю возможно большего числа 15 Основные способы получения рациональной основной системы метода сил: преобразование нагрузки Правило 1: Любую несимметричную нагрузку, действующую на симметричную раму, можно разложить на симметричное и кососимметричное составляющие. Расчет выполняется отдельно для каждого из них.
Правило 2: При симметричной внешней нагрузке действующие на симметричную раму кососимметричные силовые факторы в плоскости симметрии обращаются в ноль. В соответствии с правилом 2:
Правило 3: При кососимметричной внешней нагрузке, действующей на симметричную раму, симметричные силовые факторы в плоскости симметрии обращаются в ноль. В соответствии с правилом 3:
Правило 4: Расчет симметричной многопролетной рамы, на которую действует симметричная внешняя нагрузка, можно упростить, рассматривая половину рамы при одной оси симметрии, и ¼ часть рамы при двух осях симметрии.
Действие отброшенной части на оставшуюся учитываем введением соответствующих связей: - связь, закрепляющая сечение от поворотов в вертикальной плоскости; - связь, закрепляющая сечение от перемещений по горизонтали. 16 Основные способы получения рациональной основной системы метода сил: группировка неизвестных. При расчете многопролетных симметричных рам не всегда удается разместить все неизвестные силовые факторы в сечениях по оси симметрии. В этом случае для получения симметр. и кососимметр. требуется выбирать групповые неизвестные, расположив их а различных симметрично расположенных точках. Заданная система: двух- пролетная рама, у которой одна стойка проходит по оси симметрии
Традиционный способ решения:
Представим лишние неизвестные основной системы в виде группы сил
По правилу: (Коэффициент канонического уравнения
17 основные способы получения рациональной основной системы метода сил: введение жестких консолей. Этот способ применяется для расчета рам, имеющих замкнутый контур, и позволяет, получить системы канонических уравнений с помощью разделенных неизвестных.
Традиционная основная система: по правилу 2 δ12= δ21= δ13= δ31=0 δ23= δ32≠0
Для получения системы уравнений с полностью разделенными неизвестными необходимо так же обратить в нуль их коэффициенты: δ23= δ32 Для этого необходимо перенести неизвестные силовые факторы в точку, называемую упругим центром, с помощью бесконечно жестких консолей. Примечание: для рамы, имеющей две оси симметрии, упругий центр будет находиться на пересечении этих осей.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.160 (0.007 с.) |

 =0 (А).Эпюры
=0 (А).Эпюры  удовлетворяющие условию
удовлетворяющие условию  наз-ся взаимнонулевыми и ортогональными, поскольку при перемножении они дают 0. Существуют различ. способы получения взаимных нулевых эпюр: 1. выбор сим-ой основной сис-ы; 2. преобразование нагрузки; 3. группировка неизвестных; 4. введение жестких консолей .Примечание; Указаные способы применяются только при расчете симметричных конструкций- обладающих геометрической ижесткостной симметрией Выбор симметричной основной системы: в сим-ой осн. сист-ме все известные силовые факторы располагаются в сечении по оси симметрии в виде сим-ых и кососим-ых силовых факторов которые дадут симметр. и кососим. эпюры.Коэф-ты канонических ур-ий dik у которых один индекс принадлежит сим-му фактору, а другой кососим-му фактов, обращаются в 0.Рассмотрим сим-ую конструкцию:
наз-ся взаимнонулевыми и ортогональными, поскольку при перемножении они дают 0. Существуют различ. способы получения взаимных нулевых эпюр: 1. выбор сим-ой основной сис-ы; 2. преобразование нагрузки; 3. группировка неизвестных; 4. введение жестких консолей .Примечание; Указаные способы применяются только при расчете симметричных конструкций- обладающих геометрической ижесткостной симметрией Выбор симметричной основной системы: в сим-ой осн. сист-ме все известные силовые факторы располагаются в сечении по оси симметрии в виде сим-ых и кососим-ых силовых факторов которые дадут симметр. и кососим. эпюры.Коэф-ты канонических ур-ий dik у которых один индекс принадлежит сим-му фактору, а другой кососим-му фактов, обращаются в 0.Рассмотрим сим-ую конструкцию: 
 Сист-ма канонич-их ур-ий для этой рамы,балки будит иметь вид:
Сист-ма канонич-их ур-ий для этой рамы,балки будит иметь вид:  (1)сим-ая основная система:
(1)сим-ая основная система: 

 -косоммитр. силовой фактор,
-косоммитр. силовой фактор,  -симметр. силовые факторы.В соответствии с правилом 2 коэф-ты
-симметр. силовые факторы.В соответствии с правилом 2 коэф-ты  Тогда (1) будет иметь вид
Тогда (1) будет иметь вид  [2] Система из 3 уравн-ий распадается на две незовис системы:первая содержит кососимметр фактор, вторая-симметр силовой фактор.
[2] Система из 3 уравн-ий распадается на две незовис системы:первая содержит кососимметр фактор, вторая-симметр силовой фактор.
 , тогда система канонических уравнений будет иметь вид:
, тогда система канонических уравнений будет иметь вид: (1.1)
(1.1) , тогда 1.1 запишем в виде:
, тогда 1.1 запишем в виде: (1.2)
(1.2)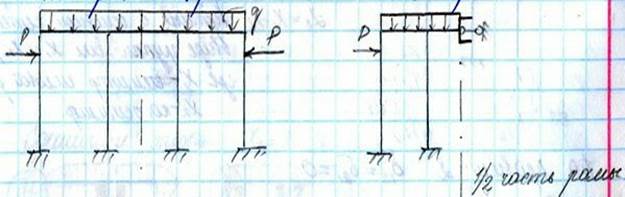


 и
и  .
. ,
,  , где
, где - симметричный силовой фактор;
- симметричный силовой фактор; 
 , у которого один индекс принадлежит симметричному фактору, а другой – кососимметричному, обращается в ноль), получаем
, у которого один индекс принадлежит симметричному фактору, а другой – кососимметричному, обращается в ноль), получаем  , в результате получаем с полностью разделенными неизвестными:
, в результате получаем с полностью разделенными неизвестными:

 традиционная основная система
традиционная основная система


