
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
расчет статически неопределимых систем методом перемещений: установление степени кинематической неопределимости.Содержание книги
Поиск на нашем сайте
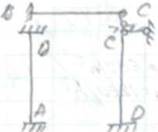
в методе перемещений за неизвестные принимаются перемещения z (линейные и угловые) узлов системы, по которым определяются внутренние усилия M,N,Q и напряжения σ в произвольном сечении. Установление степени кинематической неопределимости. Общее число неизвестных перемещений n=nу+nл, где nу- число угловых перемещений узлов; nл- число линейных перемещений узлов. Заданная система
Nл = числу независимых линейных перемещений узлов. Последовательность определения nл: 1 Превращаем систему в шарнирную систему, поставив шарниры во все узлы.
2 Превращаем полученный механизм в геометрически неизменяемую систему, путем постановки дополнительных стержней. Nл = числу введенных дополнительных стержней.
Выбор основной системы Основную систему получают из заданной путем:
- задание введенным связям соотв. угловым и линейным перемещениям Zi. 1, 2, 3 – введенные дополнительные связи; Z1, Z2, Z3 – заданные перемещения введенных связей.В качестве дополнительных связей вводятся:
Кинематическая эквивалентность основной и заданной систем достигается тем, что связям вместе с их делением задают соотв. угловые и линейные перемещения. Примечание: углы поворота введенных связей (Z1, Z2) условно задают по часовой стрелке, линейное перемещения (Z3) слева направо. Введенные связи расчленяют получаемую систему на отдельные простейшие статически неопределимые стержни – конечные элементы. Каждый из этих стержней хорошо изучен, а результаты их расчета на стандартные воздействия приводятся в справочных данных. Составляем систему конических уравнений:
где rik – коэффициент канонического уравнения (реакция i – связи от смещения; k – связи на величину Zk =1); Riр – свободный член канонического уравнения метода перемещений (реакция i – связи под действием внешней нагрузки). После определения коэффициентов и свободных членов решают систему канонических уравнений и строят окончательные эпюры М в заданной системе 20 Определения коэффициентов канонического уравнения и свободн. членов Для определения необходимо построить эпюры М неизвестных единичных перемещений Z1 =1, Z2 =1 и от внешней нагрузки. Введенные связи 1, 2 превращают основную систему в совокупность трех простейших стержней, причем каждый из стержней работает самостоятельно.
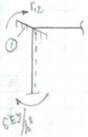
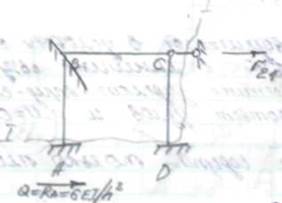
Эпюра строится индивидуально для каждого стержня по справочным данным. А) М1 (от поворота заделки 1 на угол Z1 =1 по часовой стрелке). Из справочника имеем: стержень АВ стержень ВС
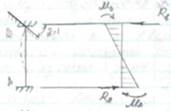
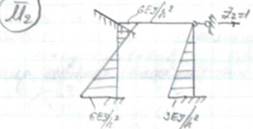
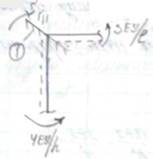
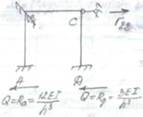
Б) построим эпюры М2 (от линейного перемещения связи 2 на угол Z2 =1 вправо). Из справочника имеем: стержень АВ стержень СD
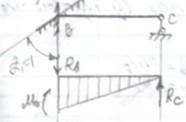
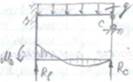
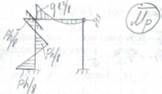
В) построим эпюры Мp (грузовая эпюра от внешней нагрузки). Из справочника имеем: стержень АВ стержень ВС
Для определения rik и Riр можно использовать 2 способа: перемножение эпюр и статический.
Определение реактивных моментов RB и RА (используемые в статическом способе) могут быть двух типов: - реактивный момент (они возникают в угловых связях); - реактивных сил (возникают в линейных связях). Реактивные моменты во введенных заделках определяется путем вырезания узлов из соответствующих узлов и Σ М =0. Примечание: вырезают узлы содержащие только плавающие заделки. узел В эпюры М1
узел В эпюры Мр
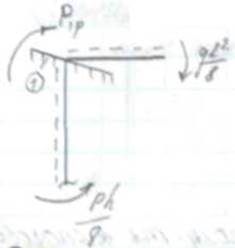
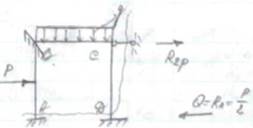
Определение реактивных сил RB и RА (используемые в статическом способе) могут быть двух типов: - реактивный момент (они возникают в угловых связях); - реактивных сил (возникают в линейных связях). Реактивные усилия во введенных стержнях определяют путем вырезанием систем рамы и составляем уравнения равновесия в виде Σ Х =0. Отсекая часть рамы эпюры М1
I-I сечение по стойкам у опорных связей введенному стержню. В местах разреза прикладываем поперечные силы, определенные через значение реакции. отсекая часть рамы эпюры М1 отсекая часть рамы эпюры Мр
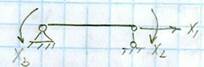
2) удаление лишних внутренних связей (рассечение стержня)
3)Переход к другим видам опорных связей (превращение заделок в другие виды опор)
4) постановка шарнира
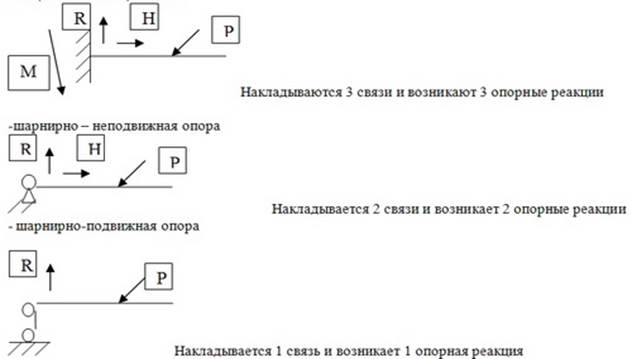
Под удалении связей необходимо следить за тем чтобы получаемая конструкция была геометрически неизменяема.В методе перемещений основную систему получают из заданной:1) введением дополнительных (фиктивных) связей устраняющих угловые и линейные перемещения узлов.2)заданием введенным связям соответствующих линейных и угловых перемещений Zi 1,2,3-введенные дополнительные связи. Z1,Z2,Z3-заданные перемещения введенных связей -угловая связь (плавающая заделка)-вводится во все жесткие узлы для устранения их поворота линейная связь –вводится для устранения линейных перемещений узлов. Эта связь соответствует связи в шарнирной геометрически неизменяемой системе. Углы поворота введенных связей условно задаются по часовой стрелке, линейные перемещения слева на право.Введенные связи расчленяют получаемую основную систему на отдельные простейшие статически неопределимые стержни - конечные элементы. 24 В методе сил степень статической неопределимости системы равна числу лишних связей, которые нужно удалить из статически неопределимой системы для обращения ее в статически определимую и геометр-ки неизменяемую. Для обеспечения неподвижности или геометр-ой неизменности балки и плоской рамы нужно наличие 3 связей. Для пространственной рамы-6 связей. Всякая связь наложенная сверх необходимых назыв. лишней или избыточной. Основные типы опорных связей для балки и плоской рамы: - защемление конца балки Накладываются 3 связи и возникают 3 опорные реакции
Накладывается 1 связь и возникает 1 опорная реакция Степень статической неопределимости для балок и плоских рам: С= m-n где m-число наложенных опорных связей или неизвестных усилий. n-нужное число связей для обеспечения геом-ой неизменяемости или число независимых уравнений статики,которые можно составить для данной системы. Степень статической неопределимости зависит от:1)числа опорных связей.2)способа приложения внешней нагрузки 3)способа соединения элементов системы(жесткая или шарнирная). Степень статической неопределимости для плоских рам имеющих замкнутый контур можно определить по формуле:С=3к,где к- число замкнутых контуров. Введение простого шарнира снимает 1 связь и снимает степень статической неопределимости на 1-цу. Степень статической неопределимости систем с шарнирами для плоских рам и балок: С= m-n-ш,а для плоских рам имеющих замкнутый контур:С=3к-ш,где ш-число простых шарниров. Простой шарнир- это шарнир в котором сходятся 2 стержня, сложный- в котором сходятся 3 и более стержней. Установление степени кинематической неопределимости. Общее число неизвестных перемещений n = nу+nл где nу- число угловых перемещений узлов, nл-число линейных перемещений узлов. Величина nу равна числу жестких узлов, а nл- равна числу независимых линейных перемещений узлов системы. Для определения nл 1)превращаем заданную систему в механизм(шарнирную систему) поставив шарниры во все узлы включая опорные.2)превращаем полученный механизм в геом-ки неизменяемую систему путем постановки дополнительных стержней. nл будет = числу введенных дополнительных стержней. 25Составление системы канонических уравнений в методе сил. Канонические уравнения характеризуют условия эквивалентности основной и заданной системы с n-лишними неизвестными. d11x1+d12x2+….d1nxn+∆1p=0 d21x1+d22x2+….d2nxn+∆2p=0 ……………………………… dn1x1+dn2x2+….dnnxn+∆np=0,где dik-коэффициент канонического уравнения(перемещение точки приложения силы xi по направлению этой же силы вызванное 1-ой силой xk=1 ∆pi- свободный член канон. уравнения(перемещение точки приложения силы xi по направлению этой силы, вызванная заданной нагрузкой Р.1-ое уравнение выражает равенство 0 суммарного перемещения точки приложения силы x1 по ее направлению.2-ое уравнение выражает равенство 0 суммарного перемещения точки приложения силы x2по ее направлению. Число уравнений должно быть равно числу отброшенных связей,т.е. числу статической неопределимости. Канонические уравнения метода перемещений имеют вид: r11Z1+r22Z2+…r1nZn+R1p=0 …………………….. rn1Z1+rn2Z2+…rn nZn+Rnp=0, где rik- коэффициент канонического уравнения метода перемещений (реакция i-ой связи от смещения k-ой связи на величину Zk=1) Rip- свободный член канон. уравнения метода перемещений (реакция i-ой связи от действия внешней нагрузки). В матричной форме система канонических уравнений имеет вид:[R]{Z}+{Rp}=0,где [R]-матрица реакций (коэффициентов канонического уравнения) r11 r12 r1n …………… R= [rn1 rn2 rnn]
{Z}-матрица –столбец неизвестных перемещений узлов Z1 {Z}= [ Z2] … Zn
{Rp}- матрица –столбец грузовых реакций(свободных членов канон.уравнения) R1p {Rp}=[ R2p] … Rnp После определения коэффициентов rik и свободных членов Ripрешают систему канон.уравнений относительно Zi, строят эпюры М в заданной системе. 26.Теория упругости(ТУ) – раздел строймеха, изучающий 𝝈. деф. состояния тел произвольной формы от произвольных внешних воздействий. В ТУ для исследования используют диф.метод. Сущность этого метода заключается в том, что тело, находящееся в равновесии под действием приложенных сил мысленно рассекают на множ. эл-ных объемов(паралелипипедов и тетраидов). Затем рассматриваются НДС каждого эл-ного объема. Тензор 𝝈— тензор второго ранга, состоящий из 9 величин составляющих 𝝈 в произвольной(•) нагруженного тела. Эти 9 величин записываются в виде табл., в которой по главной диагонали стоят 𝝈 в 3-х взаимно… осях, а в строках - 𝝉, действующие на 3-х взаимно… пл-тях. 𝝈 состояния в (•) полностью опред, если задан тензор 𝝈 этой(•). Стат. ур-ния геом ур-ния Физич ур-ния
27. Как известно в сопромате в качестве метода исследования применяется интегральный метод(метод сечения). В теории упругости(ТУ) для исследования НДС (•)-и исследования используют диф метод. Сучность метода: тело находящее в равновесии под действием приложенных сил мысленно рассекается множеством координ пл-тей на большой число ∞ малых эл-ных объемов(паралилипипед.и тетрайд.). затем рассматривается НДС каждого эл-ного объема dx;dy;dz.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.251 (0.008 с.) |

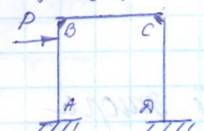 Nу = числу жестких узлов=2
Nу = числу жестких узлов=2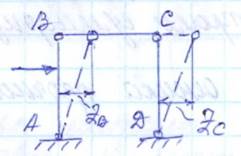

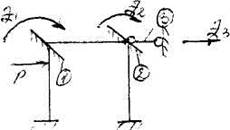 - введении дополнительных (фиктивных) связей устраняющих угловых и линейные перемещения;
- введении дополнительных (фиктивных) связей устраняющих угловых и линейные перемещения; – угловая связь, вводятся во все жесткие узлы для устранения их поворота;
– угловая связь, вводятся во все жесткие узлы для устранения их поворота; – линейная связь вводится для устранения линейных перемещений узла. Эта связь соответствует связи в шарнирной теоретически неизменяемой системы.
– линейная связь вводится для устранения линейных перемещений узла. Эта связь соответствует связи в шарнирной теоретически неизменяемой системы.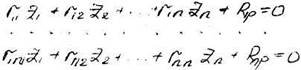
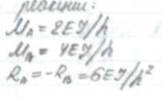
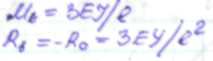
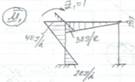


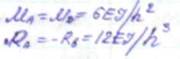
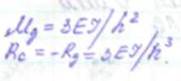
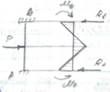
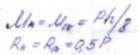
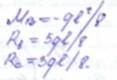

 узел В эпюры М2
узел В эпюры М2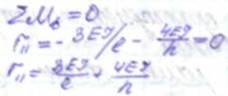
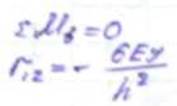
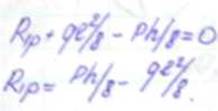


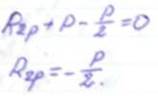

 23.Основная система – это уже статически определимая и геометрически неизменяемая система. Она получается из заданной системы в 2 этапа:1) устранение всех лишних связей 2) введение взамен удаленных связей их реакций: Х1 Х2…Хп. Для любой статически неопределимой системы всегда имеется множество вариантов основной системы. Трудоемкость расчета зависит от выбора рационального варианта основной системы. В методе сил.Варианты получения основных систем:1) удаление лишних внешних опорных связей
23.Основная система – это уже статически определимая и геометрически неизменяемая система. Она получается из заданной системы в 2 этапа:1) устранение всех лишних связей 2) введение взамен удаленных связей их реакций: Х1 Х2…Хп. Для любой статически неопределимой системы всегда имеется множество вариантов основной системы. Трудоемкость расчета зависит от выбора рационального варианта основной системы. В методе сил.Варианты получения основных систем:1) удаление лишних внешних опорных связей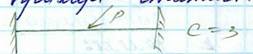

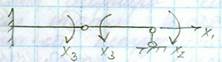
 Деформ любого эл-ного объема при рассматривании (•) можно представить в виде 6-ти простейших деформ:линейные(их 3-и εx εy εz), угловые(их 3-и γxy γyz γzx).1-е 3-и опред удлен ребер пер-да(изм объема); 2-е 3-и изм формы пер-да(деф сдвига). Совокупность деф в(•)запишем в виде матр.
Деформ любого эл-ного объема при рассматривании (•) можно представить в виде 6-ти простейших деформ:линейные(их 3-и εx εy εz), угловые(их 3-и γxy γyz γzx).1-е 3-и опред удлен ребер пер-да(изм объема); 2-е 3-и изм формы пер-да(деф сдвига). Совокупность деф в(•)запишем в виде матр.  В ТУ разделяют 3-и группы ур-ний: стат, геом, физ.
В ТУ разделяют 3-и группы ур-ний: стат, геом, физ.






