
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потоки викликів та їх характеристикиСодержание книги
Поиск на нашем сайте
4. Модели потока требований Поступающие на вход системы массового обслуживания требования (заявки, запросы) образуют поток дискретных событий, полностью определяемый множеством моментов времени их поступления В зависимости от вида функции распределения вероятности потоки требований наделяют соответствующими названиями. В общем случае случайные потоки можно классифицировать по наличию или отсутствию трех основных свойств: стационарности, последействия и ординарности. Стационарность - независимость вероятностных характеристик от времени. Так вероятность поступления определенного числа требований в интервал времени длиной t для стационарных потоков не зависит от выбора начала его измерения. Последействие - вероятность поступления требований в интервале (t1 , t2) зависит от событий, произошедших до момента t1. Ординарность - вероятность поступления двух и более требований за бесконечно малый интервал времени Δt есть величина бесконечно малая более высокого порядка, чем Δt. К основным характеристикам случайных потоков относят ведущую функцию, параметр потока и интенсивность потока. Ведущей функцией потока Параметр потока вместе с интенсивностью потока являются важнейшими характеристиками темпа поступления требований. Это плотность вероятности поступления требований в момент времени t и характеризуется тем, что вероятность поступления хотя бы одного требования в бесконечно малом промежутке времени пропорциональна с точностью до бесконечно малой более высокого порядка длине этого промежутка.
Для стационарного потока параметр потока постоянный и равен:
Интенсивность потока учитывает возможную неординарность потока, т.е. одновременно поступающие требования и определяется как математическое ожидание числа вызовов в единицу времени в данный момент. Для ординарных потоков интенсивность потока и есть его параметр.
Стационарный ординарный поток без последействия называют простейшим. Он задается набором вероятностей Pi(t) поступления i требований в промежутке длиной t.
Можно показать, что при этих предположениях формула для P i(t) дается формулой Пуассона (Poisson):
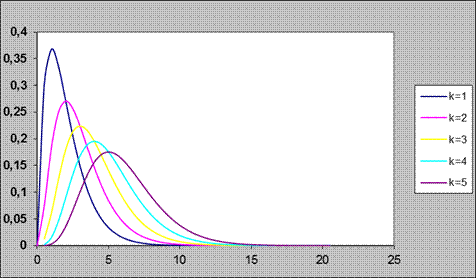
Проанализируем основные характеристики пуассоновского потока. Рассмотрим отношение Pi(t)/Pi-1(t). При i ≤ λt вероятность растет, а при обратном соотношении – убывает. Графики функции распределения Пуассона в зависимости от величины λt для различных значений k приведены на рис. 1.3.
Рис. 1.3. Графики Пуассоновского распределения в зависимости от lt для различных k. Наряду с распределением Pi(t) используют вероятности поступления не менее i требований в интервал t или не более i требований за время t:
Если рассмотреть закон распределения вероятностей промежутка между поступлением соседних требований τ, то можно показать, что
Дифференцируя, получаем плотность распределения вероятностей: Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно
а дисперсия и среднеквадратическое отклонение соответственно будут равны:
Определим математическое ожидание и дисперсию числа требований за промежуток t:
Одним из важных свойств пуассоновского потока является аддитивность.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.006 с.) |

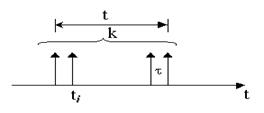
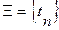 . Для детерминированного потока значения tn задаются таблицей или формулой. На практике этот поток случайный и значения моментов поступления запросов есть значения случайной величины, задаваемой функциями распределения вероятности tn либо интервала между поступлениями D t:
. Для детерминированного потока значения tn задаются таблицей или формулой. На практике этот поток случайный и значения моментов поступления запросов есть значения случайной величины, задаваемой функциями распределения вероятности tn либо интервала между поступлениями D t: 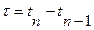 .
.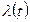 называют математическое ожидание числа требований в промежутке времени (0,t).
называют математическое ожидание числа требований в промежутке времени (0,t).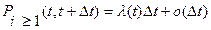 . Откуда:
. Откуда: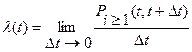 .
.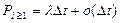 .
. Пуассоновский (простейший) поток запросов
Пуассоновский (простейший) поток запросов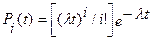 .
.
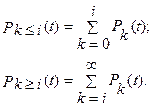
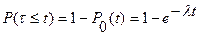 .
.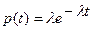 .
.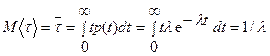 ,
,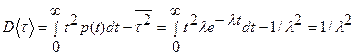 ,
,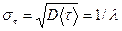 .
.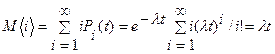 ,
,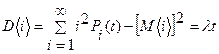 .
.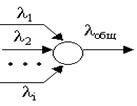 Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока
Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока 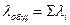 .
. 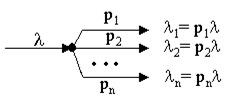 При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p i (S p i = 1 ) поступает на i- тоенаправление, поток i направления будет также пуассоновским с интенсивностью l p i.
При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p i (S p i = 1 ) поступает на i- тоенаправление, поток i направления будет также пуассоновским с интенсивностью l p i.


