
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы анализа характеристик сетей.Содержание книги
Поиск на нашем сайте Существуют два базовых метода анализа сетей Петри. Один из них основан на использовании графа достижимых маркировок (диаграммы состояний сети), другой - на применении уравнения состояний и методов линейной алгебры. Статические свойства системы определяет графовая часть сети Петри, а динамические – начальное маркирование и правила возбуждения (моделирования). Приведем определения некоторых характеристик сетей и их смысловое толкование применительно к задачам анализа систем. Маркирование Переход Переход Сеть Позицию Сеть Сеть Маркировку Сеть Сеть – непротиворечивая, а процессы в ней – детерминированные, если для всех достижимых маркирований множество переходов Проверка свойств сетей может выполняться путем построения и анализа множества достижимых состояний системы. Однако в случае большого количества состояний такой способ затруднителен. Другой способ представляет собой структурный анализ сети на основе заданной матрицы инцидентности и начального маркирования. Динамика сети в пространстве состояний может быть описана рекуррентным уравнением:
где Для решения рекуррентных уравнений смены состояний сетевых моделей используются методы линейной алгебры. Они позволяют на основе математического исследования структуры биграфа сети и начального маркирования
Е-сети. В настоящее время теория сетей Петри получила существенное развитие. Так, для описания различных и многообразных свойств систем предлагается язык нагруженных сетей, который легко адаптируется для представления различных частных классов сетевых моделей, и при необходимости объединяет эти частные свойства в едином описании. Расширением языка сетей Петри является язык вычислительных сетей, которые получили название
Рис. 5.13. Переходы В отличие от сети Петри в Определено пять типов переходов
Задачи анализа сетей Петри
Анализ заключается в изучении основных свойств сетей Петри: безопасности, ограниченности, сохранении, активности, достижимости и покрываемости. Напомним определение каждого из этих свойств.
Безопасность. Позиция piÎP сети C=(P, T, I, O, M0) является безопасной, если m(pi)£I для любой MÎR(C, M0). Сеть Петри безопасна, если безопасна каждая ее позиция. Безопасность – важное свойство для аппаратной реализации. Безопасная позиция имеет число меток 0 или 1 и может быть реализована одним триггером. Сети, в которых позиции рассматриваются (интерпретируются) как предусловия событий, маркировка каждой позиции должна быть безопасной.
Ограниченность. Безопасность – это частный случай более общего свойства ограниченности. Безопасность позволяет реализовать позицию триггером, а в более общем случае можно использовать счетчик. Любой счетчик ограничен по максимальному числу К. Соответствующая позиция также является К-безопасной или К-ограниченной, если количество меток в ней не может превысить целое число К. Позиция piÎP сети C=(P, T, I, O, M0) является К-безопасной, если m(pi)£К для всех MÎR(C, M0). Позиция называется ограниченной, если она К-безопасна для некоторого К. Сеть Петри ограничена, если все ее позиции ограничены.
Сохранение. В сетях Петри, моделирующих запросы, распределения и освобождения ресурсов, некоторые позиции могут представлять состояние ресурсов. Например, если три метки в позиции представляют три устройства (однотипных) в вычислительной системе, то интерес представляет свойство сохранения меток. То есть метки, представляющие ресурсы, никогда не создаются и не уничтожаются. Сеть Петри называется строго сохраняющей, если для всех MÎR(C, M0) выполняется условие: å m(pi) = å m0(pi). piÎP piÎP
Сеть Петри должна сохранять ресурсы, которые она моделирует. Однако не всегда имеется однозначное соответствие между меткой и количеством или числом ресурсов. В этом случае метка используется для создания кратных меток (по одной на ресурс), путем запуска перехода с большим числом выходов, чем входов. Поэтому вводятся взвешенные метки, а условие сохранения определяется через взвешенную сумму меток.
Активность. Другой задачей, возникающей при распределении ресурсов, является задача выявления тупиков. Рассмотрим на рис. 5.14 систему, включающую два различных ресурса q и r и два процесса а) и в), нуждающиеся в обоих ресурсах. Каждый процесс запрашивает ресурс, а затем освобождает его. Процесс а) сначала запрашивает ресурс q, затем ресурс r, и освобождает их. Процесс в) работает аналогично, но запрашивает сначала ресурс r, а затем q. а) в)
Рис. 5.14. Иллюстрация наличия тупика Начальная маркировка помечает ресурсы свободными и готовность процессов к работе. Выполнение сети в последовательности t1, t2, t3, t4, t5, t6 или t4, t5, t6, t1, t2, t3 не приводит к тупику. Если начать с переходов t1, t4 то выполнение заблокировано, процесс а) обладает ресурсом q и хочет получить r, процесс в) обладает r и хочет получить q. Тупик в сети Петри – это переход (или множество переходов), которые не могут быть запущены. Переходы t2 и t5 являются тупиковыми. Переход называется активным, если он не заблокирован, то есть потенциально запустимым.
Достижимость и покрываемость. Задача достижимости заключается в определении для маркировки M0 маркировки MÎR(C, M0). К этой задаче могут сводиться многие перечисленные выше задачи. Например, тупик в сети на рисунке может возникнуть, если достижимым является состояние (0, 1, 0, 0, 0, 0, 1, 0). Задача покрываемости. Для сети С с начальной маркировкой M0 и маркировки M определить, существует ли такая достижимая маркировка M’ÎR(C, M0), что M’³M. Задачи достижимости и покрываемости могут рассматриваться относительно некоторых интересующих нас подмножеств позиций.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.011 с.) |

 называют достижимым из маркирования
называют достижимым из маркирования  , если существует последовательность срабатывающих переходов
, если существует последовательность срабатывающих переходов  , переводящая сеть
, переводящая сеть  из состояния
из состояния  имеет вид:
имеет вид: 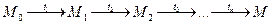 .
. называют достижимым в сети
называют достижимым в сети  , достижимое из
, достижимое из 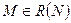 , где
, где  - множество достижимых маркирований сети.
- множество достижимых маркирований сети. называют
называют  -ограниченной, если существует неотрицательное целое
-ограниченной, если существует неотрицательное целое  :
:  , где
, где 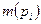 - число меток в позиции
- число меток в позиции  , то есть при всех достижимых маркированиях ее позиции не могут иметь более одной метки. Анализ безопасности проводится для исключения условий одновременного использования ресурса несколькими процессами. Например, если два сообщения о нем могут одновременно передаваться по каналу или два вычислительных процесса не могут одновременно находиться в критической программной секции, имеет место безопасность маркирования в соответствующих позициях сетевой модели.
, то есть при всех достижимых маркированиях ее позиции не могут иметь более одной метки. Анализ безопасности проводится для исключения условий одновременного использования ресурса несколькими процессами. Например, если два сообщения о нем могут одновременно передаваться по каналу или два вычислительных процесса не могут одновременно находиться в критической программной секции, имеет место безопасность маркирования в соответствующих позициях сетевой модели. , возбуждаемых маркированием
, возбуждаемых маркированием  переходов, срабатывающих при
переходов, срабатывающих при  .
. ;
;  ,
, - состояние, которое следует после состояния
- состояние, которое следует после состояния 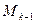 в результате
в результате  -го воздействия
-го воздействия  ;
;  - матрица, полученная транспонированием матрицы инцидентности позиций и переходов, причем ее элементы
- матрица, полученная транспонированием матрицы инцидентности позиций и переходов, причем ее элементы  равны
равны 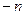 , или 0, когда соответственно переход
, или 0, когда соответственно переход  имеет
имеет  ,
,  . Если
. Если  , то в
, то в  , то срабатывание не происходит.
, то срабатывание не происходит. -сети. Так же, как и сеть Петри,
-сети. Так же, как и сеть Петри, 
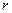 ). Каждая позиция
). Каждая позиция  -,
-,  - и
- и 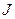 -переходы (рис. 5.13, а-в, соответственно) аналогичны переходам безопасной сети Петри.
-переходы (рис. 5.13, а-в, соответственно) аналогичны переходам безопасной сети Петри.  - и
- и  -переходы используют разрешающую позицию
-переходы используют разрешающую позицию 



