
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формализованное описание сетей Петри.Содержание книги
Поиск на нашем сайте
Для описания и математического анализа процессов с точками ветвления и синхронизации взаимодействия разработан аппарат сетей Петри. Структура сети представляется ориентированным двудольным графом. Множество Сеть Петри определяется пятеркой
Функции Дуги, предшествующие позиции Здесь запись Входные позиции перехода Маркирование сети представляется вектором Срабатывание перехода Если при маркировании
Примеры построения сети Петри . Пример 1. В примере рассматривается описание двух взаимодействующих процессов на основе механизма семафоров. Пусть в общей памяти выделен участок длиною
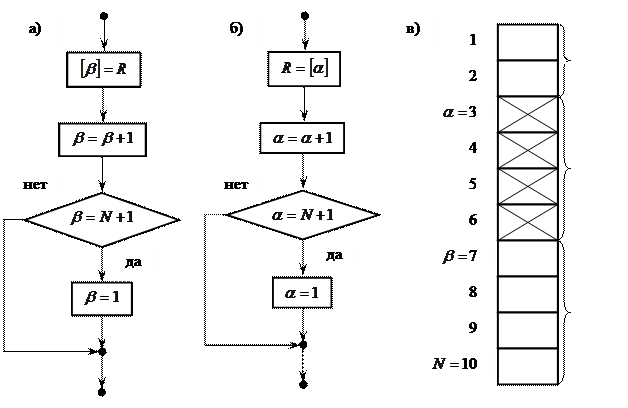
Рис. 5.9. а) – алгоритм постановки запроса в очередь; б) – алгоритм выборки запроса из очереди; в) – пример состояния очереди в буфере из
С очередью может работать несколько программ «в очередь» и «из очереди». Для организации корректного использования очереди необходимо исключить одновременный доступ программ к области хранения запросов. Иначе возможны ошибки. Например, два потребителя могут выбрать один и тот же запрос, не выбрав из очереди следующий за ним. Для исключения подобной ситуации параллельные процессы «в очередь» и «из очереди» могут синхронизироваться с помощью семафорных примитивов
Рис. 5.10. Сеть Петри, описывающая параллельные процессы управления буферированием:
Позиция Аналогично определяются операции над считывающими семафорами Пример 2. В данном примере рассматривается ВС (Рис. 5.11), содержащая процессор (П), устройство связи с объектом (УСО) и запоминающее устройство (ЗУ). УСО и П могут работать параллельно.
Рис. 5.11. Однопроцессорная ВС с УСО и ЗУ
Процессы в данной ВС порождаются периодическими и инициативными запросами от ОУ и инициативными запросами от оператора. Рассмотрим очередь запросов оператора, которые включают выполнение на П двух операций. Первая из них использует текущие данные из ЗУ. Вторая операция выполняется после первой и завершения работы УСО с ОУ и ЗУ. Сеть Петри, описывающая данный процесс, приведена на рис.5.12.
Рис. 5.12. Модель процесса в виде сети Петри
Переходы: Позиции: Переход В приведенных примерах сети Петри описывали: - параллелизм и синхронизацию процессов; - взаимодействие процессов и ресурсов, представленных метками; - независимые действия, представленные переходами; - накопители информации (ячейки и буферы) и состояния процессов, представленные позициями. Однако в рассматриваемом виде сети Петри не позволяют адекватно представлять многие свойства систем. Так, одним из недостатков сетей Петри является отсутствие времени в определении ее динамического функционирования. Большинство теоретических исследований по сетям Петри также исключает из рассмотрения время. При учете времени происходит существенное усложнение в методах анализа сетей и как бы переход от алгебраических уравнений к дифференциальным. Временные сети. Для учета временных характеристик вводятся временные сети Петри, в которых каждому переходу Раскрашенные сети. Раскрашенные сети Петри являются естественной интерпретацией реальных систем, аналогичной сетям с очередями. Однако сети с очередями не допускают представления эффектов размножения и синхронизации, отражаемых с помощью переходов в сетях Петри. Меткам раскрашенной сети Петри приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определенных цветов из позиций В ряде случаев на множестве цветов задают отношения приоритетности и сопоставляют их определенным дугам Таким образом, процедура раскраски сети Петри – это модельный способ трактовки различных по характеру реальных элементов: в алгоритмах – номера оператора или этапа обработки; в мультипрограммных системах – номера задачи, ее приоритета и других атрибутов; для ресурсов – их типа, способа использования и т.д.
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

 вершин графа разбивается на два подмножества
вершин графа разбивается на два подмножества  и
и  ,
,  ,
,  . Дугами могут связываться вершины из множеств
. Дугами могут связываться вершины из множеств  , где
, где ,
,  - множество позиций;
- множество позиций; ,
,  - множество переходов;
- множество переходов; - функция следования;
- функция следования; - функция предшествования;
- функция предшествования; - начальное маркирование (состояние) сети;
- начальное маркирование (состояние) сети; - множество положительных целых чисел.
- множество положительных целых чисел.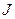 и
и  задают множества дуг
задают множества дуг  и
и  соответственно.
соответственно. , обозначим множеством
, обозначим множеством  , а дуги, предшествующие переходу
, а дуги, предшествующие переходу  , множеством
, множеством  .
. означает наличие дуги
означает наличие дуги  , а запись
, а запись  - дуги
- дуги  . Аналогично, дуги, следующие из
. Аналогично, дуги, следующие из  ,
,  .
. , а выходные позиции – в множества позиций–последователей
, а выходные позиции – в множества позиций–последователей  .
. , где
, где 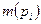 - число меток в позиции
- число меток в позиции  и может сработать, если выполняется условие
и может сработать, если выполняется условие  , то есть число меток
, то есть число меток 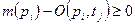 .
. теряет
теряет  меток, а каждая из позиций
меток, а каждая из позиций  получает
получает 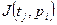 меток.
меток. единиц, который используется для хранения запросов на выполнение задач. Процессы записи запросов в очередь и выбора их из очереди могут происходить независимо (асинхронно). Описатель очереди содержит четыре элемента:
единиц, который используется для хранения запросов на выполнение задач. Процессы записи запросов в очередь и выбора их из очереди могут происходить независимо (асинхронно). Описатель очереди содержит четыре элемента:  и
и  - число заполненных и свободных ячеек очереди;
- число заполненных и свободных ячеек очереди;  и
и 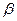 - адреса начального и конечного элементов очереди. Алгоритмы записи в очередь и выборки запросов из очереди приведены на рис. 5.9. Запись вида
- адреса начального и конечного элементов очереди. Алгоритмы записи в очередь и выборки запросов из очереди приведены на рис. 5.9. Запись вида  представляет операцию размещения в ячейку очереди с номером
представляет операцию размещения в ячейку очереди с номером  - считывание содержимого ячейки
- считывание содержимого ячейки  6
6
 4
4
 ячеек.
ячеек.
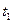 - создание запроса;
- создание запроса;  - запись запроса в очередь;
- запись запроса в очередь;  - выполнение запроса;
- выполнение запроса;  - выборка запроса из очереди.
- выборка запроса из очереди. - семафор, ограничивающий доступ процесса к очереди. Операции над
- семафор, ограничивающий доступ процесса к очереди. Операции над  - переменная
- переменная  увеличивается на 1, если
увеличивается на 1, если 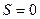 ;
;  - если
- если  , то
, то  - разрешает.
- разрешает. - если
- если 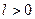 , то
, то  - если
- если  , то
, то 

 - операция 2;
- операция 2;  - подготовка ЗУ к работе (установка головок).
- подготовка ЗУ к работе (установка головок). - П свободен;
- П свободен;  - ввод данных с ЗУ в ОЗУ выполнен;
- ввод данных с ЗУ в ОЗУ выполнен;  - операция 1 выполнена;
- операция 1 выполнена;  - работа УСО закончена;
- работа УСО закончена;  - УСО свободно;
- УСО свободно;  - ЗУ готово к работе;
- ЗУ готово к работе;  - операция 2 выполнена.
- операция 2 выполнена. . Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции
. Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции  . Порождение меток в выходных позициях
. Порождение меток в выходных позициях 


