
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обнаружение тупиковых состояний.Содержание книги
Поиск на нашем сайте
Используя уравнение (5.2), условие возбуждения перехода tj можно представить в виде: n n ∑ I(tj,Pi)m(Pi) ≥ ∑ I(tj,Pi), i=1 i=1 или учитывая, что I(tj,Pi) = O*(Pi, tj), n n ∑ O*(Pi,tj)m(Pi) ≥ ∑ O*(Pi,tj). (5.13) i=1 i=1 Для краткости будем использовать векторную запись условия возбуждения переходов:
O*M ≥ O*E, где Е – единичный вектор.
Условие (5.13) объясняется следующим образом: если некоторая компонента j левой части при данном маркировании М равна соответствующей компоненте правой части или больше её, то переход tj возбуждается. Поскольку множество достижимых маркирований R(N) должно удовлетворять (5.10), то отсутствие возбуждаемых переходов для M
BM = BM0; O*M = O*E – E. (5.14)
Если эта система имеет решения, то некоторое её маркирование является тупиком. Заметим, что отношению (5.11) могут удовлетворять недопустимые маркирования, поэтому решением системы (5.14) также могут быть недопустимые маркирования, хотя все допустимые тупики удовлетворяют ему. Таким образом, система (5.14) – достаточное условие того, что маркирование М тупиково. Для анализа тупиков можно также использовать систему:
M = M0 + A*S ≥ 0; O*M ≤ O*E – E,
или
M0+ A*S ≥ 0; O*AS ≤ O*(E - M0) – E, (5.15)
если в число исходных данных входит известный вектор счёта срабатываний S. Таким образом, не совместимость системы (5.14) или (5.15) свидетельствует об отсутствии маркирования M или вектора счёта срабатываний S, которые ведут к тупику из M0 . Рассмотрим на простых примерах возможности изложенного подхода. Для сети на рис. 5.22а согласно уравнению (5.7) Р-инвариант Х является целочисленным решением системы:
- x1+ x3 = x2 + x3 = x1 + x2 – x4 = 0.
Ранг матрицы А системы АХ=0 равен трём, поэтому данная система имеет одно целочисленное базисное решение, вектор-строка которого X* = (1, -1, 1, 0). Подставив Х и M0 в равенство (5.11) BM = BM0 = K0, получим условие, верное для любого достижимого маркирования:
M = (m1, m2, m3, m4): m1 – m2 + m3 = 0 или m1+m3 = m2 .
Из последнего условия виден смысл инварианта: сумма числа меток в позициях P1, и P3 и число меток в позиции Р2 равны для любого достижимого маркирования сети. Этот инвариант верен здесь для диаграмм состояний (рис. 5.22 б, рис. 5.22 в), соответствующих разным правилам управления срабатыванием переходов. Вывод об ограниченности сети по данному значению Х сделать нельзя. Вычислим t-инварианты Y. Из системы (5.12) получим систему уравнений:
- y1 + y3 = - y2 + y3 = y1 - y2 = - y3 = 0.
Система имеет только нулевое решение Y* = (0, 0, 0), поэтому в данной сети не существует маркирований, связанных циклами на диаграмме состояний. Маркирование М совпадает с начальным, только если не срабатывает ни один из переходов сети, поскольку все компоненты вектора Y нулевые. Иначе говоря, поскольку Y =0, то последовательность состояний сети не имеет возвратов, что подтверждается диаграммами состояний. В связи с полученными особенностями целесообразно определить, имеет ли тупик указанная невозвратная последовательность маркировок. Система уравнений (5.14) имеет вид:
m1 - m2 + m3 = m1 = m4 = 0; m2 + m3 + m4 = 2.
Система совместна, и ей удовлетворяют любые маркирования, которые имеют m1=0; m2= m3; m4=0. Тупиковыми, например, являются маркирования М=(0110), М=(0220) и т. д. Таким образом, сеть номер два не является безтупиковой при M0=(1101).
Рассмотрим ещё один пример анализа.
А= Ранг матрицы А равен двум, поэтому n-2=1, т. е. в фундаментальную систему решений однородной системы АХ=0 входит один вектор Х. Распишем систему АХ=0:
x1 – x3 = x2 – x1 = x3 – x2 = 0.
Взяв её целочисленное решение X*=(1,1,1), получим условие инвариантности для позиций:
X*M = X* M0 = m1 + m2 + m3 = 1.
Интерпретация полученного результата состоит в следующем: сеть ограничена, поскольку Для вычисления t-инварианта рассмотрим систему:
y1 – y2 = y2 – y3 = y3 – y1= 0,
из которой найдём Y*=(1,1,1). Поскольку Y≠0 - сеть устойчива, т. е. процессы в ней периодически повторяются. Поскольку t-инвариант Y охватывает все переходы, так как все yi=1, то сеть жива. Система уравнений (5.14) для данной сети:
m1 + m2 + m3 = 1; m1 ≤ 0; m2 ≤ 0; m3 ≤ 0.
Поскольку она несовместна, делаем вывод, об отсутствии тупиков в данной сети. Применив описанный подход к анализу следующей сети: можно убедиться в том, что она живая, неограниченная и беступиковая.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.242 (0.007 с.) |

 R(N) следует определять из решения системы:
R(N) следует определять из решения системы:

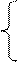


 , и, более того, - безопасна, поскольку суммарное число меток в сети не превышает 1.
, и, более того, - безопасна, поскольку суммарное число меток в сети не превышает 1.




