
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механизмы синхронизации процессов.Содержание книги
Поиск на нашем сайте
Общие сведения о сетях Петри. Исходные понятия. Сети Петри используются для моделирования асинхронных систем, функционирующих как совокупность параллельных взаимодействующих процессов. Анализ сетей Петри позволяет получить информацию о структуре и динамическом поведении моделируемой системы. Причинно-следственная связь событий в асинхронных системах задается множеством отношений вида "условия-события". Построение моделей систем в виде сетей Петри заключается в следующем: 1. Моделируемые процессы описываются множеством событий (действий) и условий определяющих возможность наступления этих событий, а также причинно-следственными отношениями, устанавливаемыми на множестве пар "события-условия". 2. Определяются события-действия, последовательность выполнения которых управляется состояниями системы. Состояния системы задаются множеством условий, формируемых в виде предикатов. Количественно условия характеризуются величиной которая выражается числами натурального ряда. 3. Условия, в зависимости от значений их количественных характеристик, могут выполняться или нет. Выполнение условий обеспечивает возможность реализации событий. Условия, с фактом выполнения которых связывается возможность реализации событий, называются предусловиями. Реализация события обеспечивает возможность выполнения других условий, находящихся с предусловиями в причинно-следственной связи. Эти условия называются постусловиями. В сетях Петри условия - это позиции, а события - переходы. В соответствии с этим граф сети Петри является двудольным ориентированным мультиграфом. Изображение позиции и перехода на графе показано на рисунке 5.1.
Рис 5.1. а) − изображение позиции; б) − изображение перехода.
Ориентированные дуги могут соединять только позиции и переходы в прямом и обратном направлении (свойство двудольности). Сеть Петри является мультиграфом, так как допускается кратность дуг между позициями и переходами (вершинами графа). Пример графа сети Петри приведен на рис.5.2. B графах сети Петри количественные характеристики условий (числа натурального ряда) принято изображать числом меток в соответствующих позициях (см. рис.5.2).
Рис.5.2. Пример графа сети Петри.
Последовательности событий отображаются срабатываниями переходов. Выполнение какого-либо условия связано с появлением одной или нескольких меток в соответствующей этому условию позиции. Соглашения о правилах срабатывания переходов является способом выражения причинно-следственных связей между условиями и событиями в системе. При моделировании гибких производственных систем позиции отражают отдельные операции производственного процесса (например: транспортировка заготовки к конвейеру, передвижение заготовки к станку конвейером, обработку детали) или состояния компонентов гибкой производственной системы (например: робота, конвейера, станка). Наличие метки в одной из позиций соответствует состоянию выполнения некоторой из технологических операций либо состояние, в котором пребывают некоторые из компонентов гибкой производственной системы. Переходы соответствуют событиям, отображающим начало или завершение моделируемых операций. Например, переход интерпретируется как событие, связанное с завершением операции транспортирования заготовки роботом и ее установки на конвейере, а также с началом операции перемещения заготовки конвейером к станку. Присвоение меток позициям сети Петри называют маркировкой сети. Динамика сетей Петри связана с механизмом изменения маркировок позиций и соглашениями о правилах срабатывания переходов. Переход срабатывает, если в каждой входной позиции (предусловии) число меток не меньше числа дуг, исходящих из позиции в данный переход. Такие переходы называют возбужденными, их срабатывание может наступить через любой конечный промежуток времени после возбуждения. В результате срабатывания из всех входных позиций перехода исключается число меток равное числу дуг, выходящих из соответствующей позиции в переход, а в выходные позиции данного перехода добавляется число меток равное числу дуг» исходящих из перехода в соответствующую выходную позицию. На рис. 5.3 а показан возбужденный переход, а перехода на рис.5.3 б невозбужден.
Рис.5.3, а − возбужденный переход, б) − невозбужденный переход.
Причем маркировка на рис.5.3 б получена в результате срабатывания возбужденного перехода на рис.5.3 а. Заметим, что срабатывание перехода предполагается неделимым актом, то есть изменение маркировок всех связанных с данным переходом входных и выходных позиций осуществляется мгновенно.
Задача о чтении/записи Рассматривается взаимодействие процессов двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий файл или переменную или элемент данных. Процессы чтения не изменяют объект, а процессы записи изменяют. Поэтому процессы записи должны взаимно исключать (см. рис. 5.4) все другие процессы чтения и записи, в то время как несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Взаимодействие процессов необходимо организовывать так, чтобы не могла возникнуть тупиковая ситуация и был обеспечен механизм взаимного исключения со стороны процессов записи.
Рис.5.7. Механизм взаимодействия процессов чтения и записи
На рис.5.7 представлена сеть Петри, имитирующая взаимодействие процессов чтения и записи при условии, что число процессов чтения и записи ограничено величиной Следует обратить внимание на то, что в данной сети позиция В тех случаях, когда число одновременно читающих процессов не ограничено, моделировать взаимодействие процессов чтения и записи с помощью сети Петри оказывается невозможным. Проблема заключается в отсутствии механизма блокировки неограниченного числа одновременно читающих процессов при выполнении процессов записи. Для хранения числа читающих процессов можно ввести специальную позицию счетчик. При запуске каждого процесса чтения в счетчик добавляется единица, а по окончании единица вычитается. Однако это не решает проблему, так как для запуска процесса записи необходимо, чтобы в позиции-счетчике отсутствовали метки. Механизма проверки неограниченной позиции на нуль в сетях Петри нет. Это показывает, что возможности сетей Петри для отображения взаимодействия процессов далеко не безграничны.
Р − и V − операции над семафорами
Одним из распространенных механизмов синхронизации процессов являются Р - и V - операции над семафорами. Семафор − это переменная, которая может принимать только неотрицательные целые значения. V - операция увеличивает значение на единицу, а Р-операция уменьшает его на единицу. Р-операция может выполняться только в том случае, когда полученное значение семафора остается неотрицательным. Таким образом, если значение семафора равно 0, то Р-операция должна ждать, пока какой-нибудь другой процесс не выполнит V -операцию. Р- и V -операции определены как примитивные, то есть никакая другая операция не может изменять значения семафора одновременно с ними. На рис.5.8 показано как такие операции моделируются сетью Петри. Каждый семафор моделируется позицией, количество меток r в позиции показывает значение семафора. Р-операции используют позицию семафора в качестве входа, а V-операции в качестве выхода.

Рис.5.8. Механизм семафоров
Примеры построения сети Петри . Пример 1. В примере рассматривается описание двух взаимодействующих процессов на основе механизма семафоров. Пусть в общей памяти выделен участок длиною
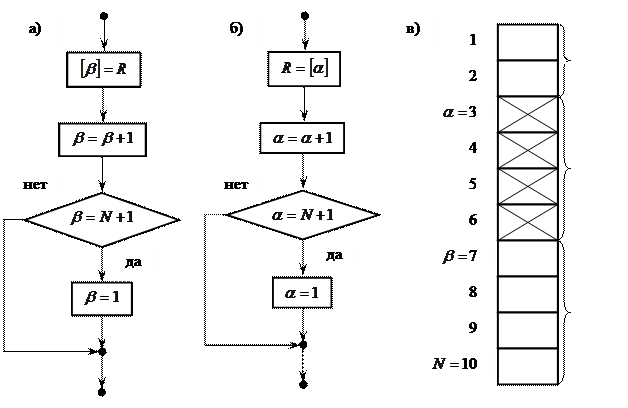
Рис. 5.9. а) – алгоритм постановки запроса в очередь; б) – алгоритм выборки запроса из очереди; в) – пример состояния очереди в буфере из
С очередью может работать несколько программ «в очередь» и «из очереди». Для организации корректного использования очереди необходимо исключить одновременный доступ программ к области хранения запросов. Иначе возможны ошибки. Например, два потребителя могут выбрать один и тот же запрос, не выбрав из очереди следующий за ним. Для исключения подобной ситуации параллельные процессы «в очередь» и «из очереди» могут синхронизироваться с помощью семафорных примитивов
Рис. 5.10. Сеть Петри, описывающая параллельные процессы управления буферированием:
Позиция Аналогично определяются операции над считывающими семафорами Пример 2. В данном примере рассматривается ВС (Рис. 5.11), содержащая процессор (П), устройство связи с объектом (УСО) и запоминающее устройство (ЗУ). УСО и П могут работать параллельно.
Рис. 5.11. Однопроцессорная ВС с УСО и ЗУ
Процессы в данной ВС порождаются периодическими и инициативными запросами от ОУ и инициативными запросами от оператора. Рассмотрим очередь запросов оператора, которые включают выполнение на П двух операций. Первая из них использует текущие данные из ЗУ. Вторая операция выполняется после первой и завершения работы УСО с ОУ и ЗУ. Сеть Петри, описывающая данный процесс, приведена на рис.5.12.
Рис. 5.12. Модель процесса в виде сети Петри
Переходы: Позиции: Переход В приведенных примерах сети Петри описывали: - параллелизм и синхронизацию процессов; - взаимодействие процессов и ресурсов, представленных метками; - независимые действия, представленные переходами; - накопители информации (ячейки и буферы) и состояния процессов, представленные позициями. Однако в рассматриваемом виде сети Петри не позволяют адекватно представлять многие свойства систем. Так, одним из недостатков сетей Петри является отсутствие времени в определении ее динамического функционирования. Большинство теоретических исследований по сетям Петри также исключает из рассмотрения время. При учете времени происходит существенное усложнение в методах анализа сетей и как бы переход от алгебраических уравнений к дифференциальным. Временные сети. Для учета временных характеристик вводятся временные сети Петри, в которых каждому переходу Раскрашенные сети. Раскрашенные сети Петри являются естественной интерпретацией реальных систем, аналогичной сетям с очередями. Однако сети с очередями не допускают представления эффектов размножения и синхронизации, отражаемых с помощью переходов в сетях Петри. Меткам раскрашенной сети Петри приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определенных цветов из позиций В ряде случаев на множестве цветов задают отношения приоритетности и сопоставляют их определенным дугам Таким образом, процедура раскраски сети Петри – это модельный способ трактовки различных по характеру реальных элементов: в алгоритмах – номера оператора или этапа обработки; в мультипрограммных системах – номера задачи, ее приоритета и других атрибутов; для ресурсов – их типа, способа использования и т.д.
Задачи анализа сетей Петри
Анализ заключается в изучении основных свойств сетей Петри: безопасности, ограниченности, сохранении, активности, достижимости и покрываемости. Напомним определение каждого из этих свойств.
Безопасность. Позиция piÎP сети C=(P, T, I, O, M0) является безопасной, если m(pi)£I для любой MÎR(C, M0). Сеть Петри безопасна, если безопасна каждая ее позиция. Безопасность – важное свойство для аппаратной реализации. Безопасная позиция имеет число меток 0 или 1 и может быть реализована одним триггером. Сети, в которых позиции рассматриваются (интерпретируются) как предусловия событий, маркировка каждой позиции должна быть безопасной.
Ограниченность. Безопасность – это частный случай более общего свойства ограниченности. Безопасность позволяет реализовать позицию триггером, а в более общем случае можно использовать счетчик. Любой счетчик ограничен по максимальному числу К. Соответствующая позиция также является К-безопасной или К-ограниченной, если количество меток в ней не может превысить целое число К. Позиция piÎP сети C=(P, T, I, O, M0) является К-безопасной, если m(pi)£К для всех MÎR(C, M0). Позиция называется ограниченной, если она К-безопасна для некоторого К. Сеть Петри ограничена, если все ее позиции ограничены.
Сохранение. В сетях Петри, моделирующих запросы, распределения и освобождения ресурсов, некоторые позиции могут представлять состояние ресурсов. Например, если три метки в позиции представляют три устройства (однотипных) в вычислительной системе, то интерес представляет свойство сохранения меток. То есть метки, представляющие ресурсы, никогда не создаются и не уничтожаются. Сеть Петри называется строго сохраняющей, если для всех MÎR(C, M0) выполняется условие: å m(pi) = å m0(pi). piÎP piÎP
Сеть Петри должна сохранять ресурсы, которые она моделирует. Однако не всегда имеется однозначное соответствие между меткой и количеством или числом ресурсов. В этом случае метка используется для создания кратных меток (по одной на ресурс), путем запуска перехода с большим числом выходов, чем входов. Поэтому вводятся взвешенные метки, а условие сохранения определяется через взвешенную сумму меток.
Активность. Другой задачей, возникающей при распределении ресурсов, является задача выявления тупиков. Рассмотрим на рис. 5.14 систему, включающую два различных ресурса q и r и два процесса а) и в), нуждающиеся в обоих ресурсах. Каждый процесс запрашивает ресурс, а затем освобождает его. Процесс а) сначала запрашивает ресурс q, затем ресурс r, и освобождает их. Процесс в) работает аналогично, но запрашивает сначала ресурс r, а затем q. а) в)
Рис. 5.14. Иллюстрация наличия тупика Начальная маркировка помечает ресурсы свободными и готовность процессов к работе. Выполнение сети в последовательности t1, t2, t3, t4, t5, t6 или t4, t5, t6, t1, t2, t3 не приводит к тупику. Если начать с переходов t1, t4 то выполнение заблокировано, процесс а) обладает ресурсом q и хочет получить r, процесс в) обладает r и хочет получить q. Тупик в сети Петри – это переход (или множество переходов), которые не могут быть запущены. Переходы t2 и t5 являются тупиковыми. Переход называется активным, если он не заблокирован, то есть потенциально запустимым.
Достижимость и покрываемость. Задача достижимости заключается в определении для маркировки M0 маркировки MÎR(C, M0). К этой задаче могут сводиться многие перечисленные выше задачи. Например, тупик в сети на рисунке может возникнуть, если достижимым является состояние (0, 1, 0, 0, 0, 0, 1, 0). Задача покрываемости. Для сети С с начальной маркировкой M0 и маркировки M определить, существует ли такая достижимая маркировка M’ÎR(C, M0), что M’³M. Задачи достижимости и покрываемости могут рассматриваться относительно некоторых интересующих нас подмножеств позиций.
Модификации сетей Петри
Временная сеть Петри
Такая сеть позволяет более реалистично отражать процессы в ВС. Во временных сетях каждому переходу tj сопоставляется время τj. Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции Pre(tj). Порождение меток в выходных позициях Post(tj) происходит через время τj. Формальное определение временной сети: TN = {N, τ}, где N - сеть Петри; τ: T → R0 -функция времён срабатывания, сопоставляющая каждому переходу постоянное время срабатывания; R0 - множество неотрицательных рациональных чисел.
Пример взаимодействия двух узлов сети ЭВМ Рассмотрим пример модели взаимодействия между узлами сети ЭВМ, описывающей протокол связи с исправлением ошибки, рис. 5.17. Протокол предусматривает подтверждение приёма посланного сообщения, повторение передачи при потере сообщения и соответствует упрощенной версии реального протокола. Содержательный смысл, соответствующий состояниям и переходам сети Петри, имеет определённые значения. Переходам tj сопоставлены времена τj, отражающие длительность выполнения соответствующих действий в системе обработки и обмена, генераторах помех и тайм-аута. отношения приоритетности введены для двух пар переходов – (t2,t8) и (t7,t11), поскольку только по отношению к ним может возникнуть конфликт за метку. Они имеют вид:
PR(t8) > PR(t2) и PR(t7) > PR(t11).
ПрП – процессор-приёмник; ГТ – генератор тайм-аута; ИП – источник помех; t1 - передача сообщений в буфер обмена; t2 - приём сообщения; t3 - посылка подтверждения о приёме данных; t4 - приём подтверждения; t5 - обработка данных в ПрИ; t6 - обработка в ПрП; t7 - повторение передачи; t8, t9 - переходы модели источника помех; t10, t11 - элементы ГТ; P1 - конец обработки в ПрИ и запрос действия t1; P2 - буфер сообщения; P3 - ПрП готов принять сообщение и запрашивает t2; P4 - ПрИ ожидает подтверждения; P5 - завершение действия t2 и запуск t3; P6 - запрос t6; P7 - буфер подтверждения; P8 - запрос t5; P9, P10 - позиции ГТ; P11, P12 - позиции ИП;
Рис. 5.17. Пример временной сети Петри с приоритетами. Передача сообщения процессором-источником порождает буферирование копии сообщения и запуск генератора тайм-аута, посылку сообщения в канал, а также формирование условия подтверждения о приёме, что отражается появлением меток в P2, P4, P9. Если сообщение в канале P2 исчезнет благодаря действию ИП (что отражается возбуждением t8), то не приходит подтверждение приёма (метка в P7 не появится), и через время тайм-аута (связанное с t10) произойдёт повторная выдача сообщения в канал (что отражается срабатыванием t7). С t9 связан интервал времени между потерей в канале очередного сообщения и возникновением условия для потери следующего сообщения. С t10 связано время тайм-аута, через которое организуется повторная посылка потерянного сообщения. Если через τ10 в P4 нет метки, то не создадутся условия возбуждения t7 и метка из P10 покинет ГТ.
Рис. 5.18. Граф допустимых маркирований
На рисунке изображён граф допустимых маркирований элементов модели ПрП и ПрИ. В вершинах графа состояний перечислены наборы позиций, в которых одновременно находятся метки-сообщения, полученные для начального маркирования M0. Ориентированные дуги указывают переходы между состояниями системы, а пометки у дуг указывают на переходы t, срабатывание которых вызывает данное изменение состояния. Пример показывает, что вместо длинных словесных описаний протокола взаимодействия достаточно иметь графическое изображение модели, спецификацию времени и приоритетов, обеспечивая тем самым всю информацию о возможных путях и свойствах процессов. Пренебречь временными свойствами сети возможно только в том случае, если исключение τ не отразится на структуре переходов диаграммы состояний сети. В данном случае невозможно пренебречь временными характеристиками, не исказив представление возможных свойств объекта.
Раскрашенные сети
Такие сети являются естественной интерпретацией реальных систем, аналогичной многоклассовым сетям с очередями. Однако эти многоклассовые сети не допускают представления эффектов размножения и синхронизации, отражаемых с помощью переходов в сетях Петри. Метками раскрашенной сети приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определённых цветов из позиций Pre(tj). Срабатывание переходов сопровождается посылкой в позиции Post(tj) меток, с задаваемыми значениями цвета.
t1, t2 - загрузка процессоров; t3, t4 – обработка; t5, t6 - освобождение процессоров P0 - позиция супервизора; P1, P2 - заявки на обработку; P3, P4 - Заявки приняты; P5, P6 - конец обработки; P7, P8 - обработанные заявки; P9, P10 - двоичные семафоры, исключающие запуск занятых процессоров.
Рис. 5.19. Пример раскрашенной сети для двухпроцессорной системы.
На Рис.5.19 приведена модель процессов в двухпроцессорной системе, управляемой супервизором. Множество атрибутов-цветов, связываемых с метками и дугами сети, принято равным С = {λ, C1, C2, C3, C4}. В сети раскрашена метка, имитирующая работу супервизора и дуги, имитирующие последовательность запуска процессоров. Прочие дуги, а также метки-заявки и метки управления не нарушены. Начальный цвет метки в P0 равен C1 и дуга (P0,t1) окрашена в C1. Поэтому условие возбуждения выполнимо для перехода t1. После срабатывания t1 в P0 метка возвращается, уже имея цвет C2, поскольку дуга (t1,P0) раскрашена в цвет C2. Раскрашивание дуг обеспечивает возбуждение только одного из переходов, следующих за P0, при любом состоянии системы. При данной раскраске алгоритм работы супервизора представлен последовательностью срабатывания переходов t1, t2 (t3, t4) t5, t6, т. е. происходит запуск первого процессора, затем второго, после чего следует их освобождение и цикл повторяется.
Рис. 5.20. Пример раскрашенной сети: а) – граф алгоритма; б) – биграф алгоритма; в) – модель мультипрограммного выполнения алгоритмов, представленная раскрашенной сетью.
В примере 2 раскрашенная сеть используется для представления мультипрограммного выполнения алгоритма с ветвями и точкой синхронизации в ВС с процессором и УВВ. На Пр и УВВ параллельно могут выполняться операторы 2 и 3, завершение которых является условием выполнения оператора 0, что видно из рис.5.20а. Переходы t0 – t3 биграфа (рис. 5.20б) соответствуют вершинам графа на рис. 5.20а. Для отображения точки входа в алгоритм на его биграфе введена маркированная позиция P1, поэтому нулевой вершине графа (рис. 5.20а) поставлены в соответствие переходы t0 и t4 биграфа. При построении сети (рис. 5.20в) учтено, что время выполнения операций t1 и t4 мало по сравнению с остальными. Учитывая также, что действия t0 и t2 выполняются на процессоре, позиции P1 и P5, а также P2 и P6 биграфа совмещены на рис.5.20в и обозначены как P1 и P2. Процессы выполнения алгоритмов представлены движением меток. Раскраска меток двухэлементная, определяющая номер процесса a = {1, 2, 3} и номер этапа обработки C = {C0, C1, C2, C3}. Из рис. 5.20в видно, что некоторые из дуг раскрашены одним цветом (Ci), другие парой цветов (a Ci), третьи не раскрашены вовсе, что учитывается при управлении возбуждением переходов и изменении цвета меток. Заметим, что при раскрашивании парой цветов все эти признаки анализируются или изменяются в комплексе. Например, входные дуги перехода t4 помечены парами a C2 и a C3, что определяет выбор для синхронизации на t4 процессов с одним и тем же номером a и завершенными этапами обработки C2 и C3 соответственно. Следующий пример (рис. 5.21) показывает изобразительные возможности раскрашенных сетей по разделению путей данных и управления в УВВ. Данные от двух источников U1 и U2 помечены квадратами в P1 и P3, а сигналы запроса на обработку – кружками в P2 и P4. Запросы принимаются (переходы t1, t2), накапливаются в регистре (позиция P5), выбираются из неё (переход t3) и запускают пересылку данных от источников (P1 или P3) в буфер P7. Метка-треугольник в позиции P8 отражает управляющий процесс, разрешающий выполнение только одной из двух операций считывания t4 или t5. Читателю предлагается самостоятельно разобраться, почему необходимо использовать раскрашенную метку в позиции P8 и на дугах
Рис. 5.21. Пример сети с разделением передачи данных
Таким образом, процедура раскраски сети Петри – это модельный способ трактовки различных по характеру реальных элементов: - в алгоритмах – номера оператора или этапа обработки; - в мультипрограммных системах – номера задачи, её приоритета и других атрибутов; - для ресурсов – их типа, способы использования и т. п.
Общие сведения о сетях Петри. Исходные понятия. Сети Петри используются для моделирования асинхронных систем, функционирующих как совокупность параллельных взаимодействующих процессов. Анализ сетей Петри позволяет получить информацию о структуре и динамическом поведении моделируемой системы. Причинно-следственная связь событий в асинхронных системах задается множеством отношений вида "условия-события". Построение моделей систем в виде сетей Петри заключается в следующем: 1. Моделируемые процессы описываются множеством событий (действий) и условий определяющих возможность наступления этих событий, а также причинно-следственными отношениями, устанавливаемыми на множестве пар "события-условия". 2. Определяются события-действия, последовательность выполнения которых управляется состояниями системы. Состояния системы задаются множеством условий, формируемых в виде предикатов. Количественно условия характеризуются величиной которая выражается числами натурального ряда. 3. Условия, в зависимости от значений их количественных характеристик, могут выполняться или нет. Выполнение условий обеспечивает возможность реализации событий. Условия, с фактом выполнения которых связывается возможность реализации событий, называются предусловиями. Реализация события обеспечивает возможность выполнения других условий, находящихся с предусловиями в причинно-следственной связи. Эти условия называются постусловиями. В сетях Петри условия - это позиции, а события - переходы. В соответствии с этим граф сети Петри является двудольным ориентированным мультиграфом. Изображение позиции и перехода на графе показано на рисунке 5.1.
| |||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 а) б)
а) б)


 а) б)
а) б)
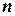 . Это означает, что и при неограниченном числе процессов чтения, одновременно могут выполняться не более
. Это означает, что и при неограниченном числе процессов чтения, одновременно могут выполняться не более  процессов чтения и
процессов чтения и  процессов записи. Из данной сети видно, что процессы находятся в конфликте за метку в позиции
процессов записи. Из данной сети видно, что процессы находятся в конфликте за метку в позиции  . При захвате меток процессом записи позиция
. При захвате меток процессом записи позиция  единиц, который используется для хранения запросов на выполнение задач. Процессы записи запросов в очередь и выбора их из очереди могут происходить независимо (асинхронно). Описатель очереди содержит четыре элемента:
единиц, который используется для хранения запросов на выполнение задач. Процессы записи запросов в очередь и выбора их из очереди могут происходить независимо (асинхронно). Описатель очереди содержит четыре элемента:  и
и  - число заполненных и свободных ячеек очереди;
- число заполненных и свободных ячеек очереди;  и
и 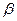 - адреса начального и конечного элементов очереди. Алгоритмы записи в очередь и выборки запросов из очереди приведены на рис. 5.9. Запись вида
- адреса начального и конечного элементов очереди. Алгоритмы записи в очередь и выборки запросов из очереди приведены на рис. 5.9. Запись вида  представляет операцию размещения в ячейку очереди с номером
представляет операцию размещения в ячейку очереди с номером  - считывание содержимого ячейки
- считывание содержимого ячейки  6
6
 4
4
 ячеек.
ячеек. и
и  . Сеть Петри, описывающая эти параллельные процессы, приведена на рис. 5.10. Содержательный смысл позиций и переходов отражен у этих элементов сети.
. Сеть Петри, описывающая эти параллельные процессы, приведена на рис. 5.10. Содержательный смысл позиций и переходов отражен у этих элементов сети.
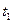 - создание запроса;
- создание запроса;  - запись запроса в очередь;
- запись запроса в очередь;  - выполнение запроса;
- выполнение запроса;  - выборка запроса из очереди.
- выборка запроса из очереди. - семафор, ограничивающий доступ процесса к очереди. Операции над
- семафор, ограничивающий доступ процесса к очереди. Операции над  - переменная
- переменная  увеличивается на 1, если
увеличивается на 1, если 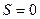 ;
;  - если
- если  , то
, то  - разрешает.
- разрешает. - если
- если 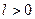 , то
, то  - если
- если  , то
, то 

 - операция 2;
- операция 2;  - подготовка ЗУ к работе (установка головок).
- подготовка ЗУ к работе (установка головок). - П свободен;
- П свободен;  - ввод данных с ЗУ в ОЗУ выполнен;
- ввод данных с ЗУ в ОЗУ выполнен;  - операция 1 выполнена;
- операция 1 выполнена;  - работа УСО закончена;
- работа УСО закончена;  - УСО свободно;
- УСО свободно;  - ЗУ готово к работе;
- ЗУ готово к работе;  - операция 2 выполнена.
- операция 2 выполнена. сопоставляется время
сопоставляется время  . Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции
. Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции  . Порождение меток в выходных позициях
. Порождение меток в выходных позициях  происходит через время
происходит через время  . Правила возбуждения перехода
. Правила возбуждения перехода 








 и
и  .
.



