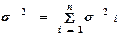Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервні випадкові величини – НВВ. Означення інтегральної функції розподілу та доведення її властивостей.Содержание книги
Поиск на нашем сайте
ВВ називається неперервною (НВВ), якщо її інтегральна функція неперервна. ВВ називається дискретною (ДВВ), якщо її інтегральна функція розривна (кусочно – стала). Інтегральною функцією розподілу F(X) ВВ X називається імовірність того, що ВВ прийме значення, менше від числа x, тобто
1. Значення функції належать проміжку [0.1], тобто Доведення: 2. Функція є неспадною, тобто Доведення:
Наслідок (основна формула теорії ймовірностей):
3.Імовірність того, що НВВ Х прийме деяке окреме значення дорівнює нулю, тобто P(X=x1)=0 Доведення:
Наслідок. Для НВВ
Означення диференціальної функції розподілу (щільності розподілу імовірностей) та доведення її властивостей. Щільністю розподілу ймовірностей (або диференціальною функцією розподілу) називається похідна (якщо вона існує) від інтегральної функції розподілу:
ВЛАСТИВОСТІ ДИФЕРЕНЦІАЛЬНОЇ ФУНКЦІЇ.
1. Щільність розподілу імовірностей – невід’ємна функція, тобто Доведення:
2.Теорема. (основна формула теорії імовірностей). Імовірність того, що НВВ X прийме значення із деякого проміжка (a;b) знаходиться за формулою:
2. Інтегральна функція розподілу та диференціальна (щільність розподілу імовірностей) є еквівалентними узагальненими характеристиками НВВ, які пов’язані співвідношенням: Доведення:
3. Умова нормування закону розподілу НВВ має вигляд: Доведення:
12. Закон рівномірного розподілу, або рівномірний закон. Інтегральна функція розподілу імовірностей для рівномірного розподілу ймовірностей. Математичне сподівання та дисперсія для рівномірного закону. НВВ X називається рівномірно розподіленою на проміжку [a,b], якщо її щільність розподілу імовірностей стала на цьому проміжку, а поза цим проміжком дорівнює нулю, тобто
Графік:
Закон показникового розподілу, або показниковий закон. Інтегральна функція розподілу ймовірностей для показникового закону. Математичне сподівання та дисперсія для показникового закону. НВВ X називається розподіленою за показниковим законом з параметром
інтегральна функція розподілу
Графіки цих функцій:
Нормальний закон розподілу. Вивести формулу для імовірністі попадання значень нормально розподіленої випадкової величини до заданого проміжку, наслідок. Правило “трьох сигм”. НВВ X розподілена за нормальним законом з параметрами a та
Скористувавшись означеннями, неважко переконатись, що числові характеристики нормально розподіленої ВВ дорівнюють:
Інтегральна: Імовірність попадання значень нормально розподіленої ВВ X до проміжку [x1;x2] знаходиться за формулою:
Правило трьох сигм. Із практичною достовірністю (з імовірністю 0,9973) можна стверджувати, що значення нормально розподіленої ВВ X попадають до проміжка Доведення:
Закон великих чисел. Центральна гранична теорема. Інтегральна теорема Муавра-Лапласа. Частинні випадки теореми Муавра-Лапласа. Нерівність Маркова. Нерівність Чебишева. Частинні випадки нерівності Чебишева. Теорема Бернуллі. Збіжність за ймовірністю. Теорема Чебишева. Закон великих чисел із уточненням Ляпунова. Центральна гранична теорема-якщо всі ВВ однаково розподілені, то закон розподілу їх суми при Інтегральна теорема Муавра-Лапласа. Для біноміально розподіленої ДВВ X=m - частоти появи події A з імовірністю p в серії із n НПВ справедлива наближена формула:
де Ф(t) - інтегральна функція Лапласа. Частинні випадки інтегральної теореми Муавра-Лапласа. Для частоти m та частості m/n появи події A з імовірністю p в серії із n НПВ справедливі наближені формули:
Якщо ВВ X приймає тільки невід’ємні значення і має фіксоване математичне сподівання M(X), то для довільного додатного числа a справедлива нерівність:
Теорема (нерівність Чебишова). Якщо довільна ВВ x має фіксовані математичне сподівання M(X) та дисперсію D(X), то для довільного додатного числа
ЧАСТИННІ ВИПАДКИ НЕРІВНОСТІ ЧЕБИШОВА.
а) для біноміально розподіленої ДВВ X = m - частоти появи події A з імовірністю p в серії із n НПВ:
б) для біноміально розподіленої ДВВ
Теорема Бернуллі Частість m/n появи події A в серії із n НПВ при
Послідовність називається збіжною за імовірністю до величини a (сталої або випадкової), якщо для довільного як завгодно малого числа
Теорема Ляпунова. Тоді закон розподілу суми
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.184 (0.009 с.) |

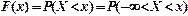
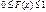 ,причому
,причому 
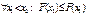
 .
. справедливі рівності:
справедливі рівності:

 .
.



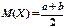
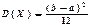
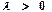 , якщо її щільність розподілу імовірностей має вигляд
, якщо її щільність розподілу імовірностей має вигляд



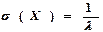
 , якщо її щільність розподілу імовірностей має вигляд:
, якщо її щільність розподілу імовірностей має вигляд:

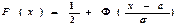
 Доведення:
Доведення: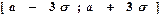 .
.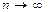 необмежено наближається до нормального.
необмежено наближається до нормального. ,
,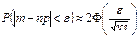 ,
,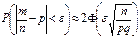

 справедлива нерівність:
справедлива нерівність: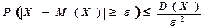
 ,або
,або 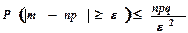 ;
; - частості (частки) появи події A в серії із n НПВ:
- частості (частки) появи події A в серії із n НПВ: , або
, або 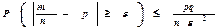
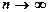 збігається за імовірністю до p = P(A) - імовірності появи події у кожному окремому випробуванні:
збігається за імовірністю до p = P(A) - імовірності появи події у кожному окремому випробуванні:

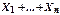 при
при 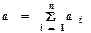 і дисперсією
і дисперсією