
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретні випадкові величини – двв. Закони розподілу ймовірностей для двв. Операції над дискретними випадковими величинами.Содержание книги
Поиск на нашем сайте
Випадковою величиною (ВВ) називається величина, яка в результаті випробування в залежності від випадкових обставин може набувати деякого (але тільки одного) значення. Дискретною випадковою величиною (ДВВ) називається ВВ, яка може приймати окремі ізольовані значення з певними ймовірностями (причому кількість можливих значень або скінченна, або нескінченна, але злічена). На відміну від ДВВ, значення неперервних ВВ повністю заповнюють деякий проміжок (скінченний або нескінченний). ВВ вважається заданою, якщо задано її закон розподілу. Законом розподілу ДВВ називається відповідність між множиною її можливих значень та відповідними імовірностями (тобто, імовірностями, з якими можуть набуватись ці значення). Основними способами задання законів розподілу ДВВ є табличний, графічний та аналітичний. ДВВ задано таблицею: Хі- можливі різні значення ВВ Х; pі – відповідні ймовірності Наочною формою задання ДВВ є графічний спосіб, при якому в системі координат XoP відкладають точки (Xi;pi) і з’єднують їх відрізками. При аналітичному способі задання закону розподілу ДВВ X вказують формулу (функцію), за якою знаходяться відповідні ймовірності Добутком ВВ X на сталий множник k називається ВВ kX, яка набуває можливих значень kxi з тими ж імовірностями pi, що і ВВ X. k- им степенем (k=2,3….) ВВ X називається ВВ Сумою (різницею або добутком) двох незалежних ВВ X та Y називається ВВ X+Y (X-Y або XY), яка приймає всі можливі значення xi + pj (xi - yj або xiyj) з ймовірностями pij, що знаходяться за теоремою добутку:
Математичне сподівання дискретної випадкової величини та його властивості. Довести (на вибір) три з них. Математичним сподіванням (середнім значенням або центром розподілу) ДВВ X називається сума добутків всіх її значень на відповідні ймовірності, тобто ВЛАСТИВОСТІ МАТЕМАТИЧНОГО СПОДІВАННЯ. 1. МС сталої ВВ дорівнює самій цій сталій: M(c)=c Доведення:
2. Сталий множник виноситься за знак МС: M(cX)=cM(X) Доведення: 3. МС суми ВВ дорівнює сумі їх МС: M(X+Y)=M(X)+M(Y) Наслідок. МС різниці ВВ дорівнює різниці їх МС: M(X-Y)=M(X)-M(Y) 4. МС добутку (незалежних) ВВ дорівнює добутку їх МС: M (XY)=M(X)M(Y). 5. МС центрованої ВВ X-M(X) дорівнює нулю:M[X-M(X)]=0. Доведення: Дисперсія дискретної випадкової величини та її властивості. Довести (на вибір) три з них. Середнє квадратичне відхилення. Дисперсією ДВВ називається МС квадрата відхилення ВВ від свого МС, тобто:
Дисперсія (якщо вона існує) має розмірність квадрата ВВ, є невипадковою сталою невід’ємною величиною, що характеризує розсіювання значень ВВ від центру розподілу – МС. 1. Дисперсію можна знаходити за формулою:
2. Дисперсія сталої дорівнює нулю: D(C)=0 Доведення. D(c)= 3. Сталий множник виноситься за знак дисперсії в квадраті: D(cX)=c^2D(X). Доведення. D(cX)= за 1 власт.= M[(cx)^2 – M^2 [cx]= за вл. МС= 4. Дисперсія суми незалежних ВВ дорівнює сумі їх дисперсій: Наслідок. Дисперсія різниці незалежних ВВ дорівнює сумі їх дисперсій: D(X-Y)=D(X)+D(Y) Наслідок. Дисперсія центрованої ВВ X-M(X)співпадає із дисперсією самої ВВ X, а дисперсія стандартизованої ВВ 5. Якщо ВВ X та Y залежні, то: 6. Дисперсія добутку незалежних ВВ дорівнює: D(XY)=M(X^2)M(Y^2)-M^2(X)M^2(Y). 7. Дисперсія середнього арифметичного незалежних ВВ дорівнює:
Важливий висновок: при вимірюваннях (дослідженнях) в якості остаточного результату беруть середньоарифметичну усіх результатів. При цьому похибки від точного значення зменшуються на к-сть результату. Для того, щоб мати аналогічну характеристику такої ж розмірності як сама ВВ, розглядають середнє квадратичне відхилення (стандарт):
Незалежні повторні випробування – НВП. НВП як випробування, проведені за схемою “повернених куль”. Виведення формул для математичного сподівання, дисперсії та середнього квадратичного відхилення частоти та відносної частоти в схемі незалежних повторних випробувань. Означення. Якщо серію n випробувань проводити в однакових умовах і імовірність появи події A в кожному окремому випробуванні однакова та не залежить від появи або непояви події A в інших випробуваннях, то таку послідовність НПВ називають схемою Бернуллі. Прикладами НПВ є: кидки монети (подія A - випадіння цифри), діставання кулі за схемою «повернених куль» із урни з різнокольоровими кулями (подія A - діставання кулі певного кольору), контроль якості серії виготовлених автоматом деталей (подія A - бракована деталь) тощо. Теорема. Нехай проводиться n НПВ за схемою Бернуллі і ймовірність появи події A в кожному із випробувань p = P(A) незмінна (ймовірність непояви події A в кожному із випробувань
9.Формула Бернуллі. Біноміальний закон розподілу ймовірностей (закон Бернуллі). Найімовірніша частота (мода) настання події. Локальна теорема Лапласа. Формула Пуассона. Закон рідкісних подій (закон Пуассона).
Біноміальным законом розподілу ДВВ X називають ДВВ X = m – частоту появи події A у n НПВ, таблиця розподілу якої має наступний вигляд
M(m) = np; D(m) = npq; Найімовірнішою частотою m0 (або модою) появи події A у n НПВ називають частоту, для якої За означенням із системи умов
неважко дістати подвійну нерівність для визначення найімовірнішої частоти:
Теорема (локальна формула Муавра-Лапласа). Якщо у схемі Бернуллі із n НПВ імовірність появи події A дорівнює p (0 < p < 1), а кількість НПВ досить велика, то імовірність появи події A m разів у n НПВ наближено дорівнює (тим точніше, чим більше n):
Формула Пуассона:
Означення. При виконанні умов теореми Пуассона ВВ Х = m (яка приймає нескінченну злічену множину значень m = 0,1,2///, а відповідні імовірності знаходяться за формулою
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.125.240 (0.022 с.) |

 , або задають так звані функції розподілу.
, або задають так звані функції розподілу. , яка приймає значення
, яка приймає значення  з тими ж імовірностями pi, що і ВВ X.
з тими ж імовірностями pi, що і ВВ X.

 .
. .
. Доведення:
Доведення: за власт. МС = c^2-c^2=0
за власт. МС = c^2-c^2=0
 .
. дорівнює одиниці.
дорівнює одиниці. , де
, де  - коваріація між ВВ X та Y.
- коваріація між ВВ X та Y.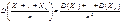 .
.
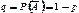 ). Тоді імовірність того, що подія A з’явиться m разів у n НПВ
). Тоді імовірність того, що подія A з’явиться m разів у n НПВ  знаходиться за формулою Бернуллі:
знаходиться за формулою Бернуллі:






 .
.
 .
.

 де a = const >0) називають розподіленою за законом Пуассона (закон рідкісних подій).
де a = const >0) називають розподіленою за законом Пуассона (закон рідкісних подій).


