
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ альтернатив действий в условиях определенности
МЕТОД ЭКОНОМИКО-МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Это самый простой случай: известно количество возможных ситуаций (вариантов) и их исходы. Нужно выбрать один из возможных вариантов. Степень сложности процедуры выбора в данном случае определяется лишь количеством альтернативных вариантов и количеством критериев. При однокритериальном применяется метод «прямого счета». При этом последовательность действий ЛПР следующая: · определяется критерий, по которому будет делаться выбор; · методом “прямого счета” исчисляются значения критерия для сравниваемых вариантов; · вариант с лучшим значением критерия рекомендуется к отбору. Процедурная сторона анализа существенно усложняется из-за множественности критериев, техника “ прямого счета “ в этом случае практически не применима. Наиболее целесообразным методом принятия решений становится метод экономико – математического моделирования. Содержание экономико-математических моделей и методика их построения Наиболее полное законченное определение экономико-математической модели дал академик В.С.Немчинов: «Экономико-математическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме». Экономико-математические модели включают в себя систему ограничений и целевую функцию. Если при этом математическая постановка задачи состоит в определении наибольшего или наименьшего значения целевой функции, то данная задача называется экстремальной. При решении экстремальных экономических задач критерии оптимальности отражаются в математических зависимостях, имеющих вид уравнений, поэтому уравнения критерия оптимальности называются уравнениями цели, или целевыми функциями. Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция – функция многих переменных величин и может иметь свободный член. Каждой экономической экстремальной задаче соответствует одна целевая функция.
Модель экономической или производственной задачи должна отражать конкретные условия деятельности предприятия, поэтому для такой модели необходимы кроме целевой функции дополнительные условия, выраженные, например, уравнениями и неравенствами. Эти уравнения и неравенства составляют систему ограничений, а сами уравнения и неравенства называются ограничительными. Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами. Критерий оптимальности – экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции. Смешивать понятия критерия оптимальности и целевой функции нельзя. Критерий оптимальности есть понятие модельное, экономическое. Критерии оптимальности могут быть натуральные и стоимостные. Одни из критериев – максимизируемые, другие – минимизируемые. Минимизируемым критерием является критерий совокупных затрат всех видов (труда, сырьевых ресурсов и т.д.). Из максимизируемых критериев можно выделить такие, как: число наборов конечных продуктов, валовая, конечная, чистая и условно чистая продукция, прибыль, рентабельность и др. Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения. Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначать искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям и т.д. Как правило, для обозначения переменных величин используются буквы: x, y, z, а также их модификации. Например, модификация переменной х: х1, хij и т.д. Аналогичные модификации могут быть и для других переменных, используемых в модели. Переменные х1, х2, …, хn могут обозначать объемы производства продукции соответственно первого, второго и так далее n-го вида. По каждой переменной для конкретной задачи дается словесное пояснение.
Целевую функцию – цель задачи – чаще всего обозначают буквами f, F, Z. Постоянные величины обычно обозначают буквами: a, b, c, d и т.д. Ограничения модели должны отражать все условия, формирующие оптимальный план. Однако практически учесть все условия задачи для достижения цели невозможно, достаточно учесть основные условия. Естественно, полученная модель будет упрощенной по сравнению с реальной, которая отражала бы все условия поставленной задачи. Итак, в упрощенном виде экономико-математическая модель представляет собой: ü систему ограничений - равенства, неравенства вида больше или равно ü условия неотрицательности переменных, исходя из экономической или физической сущности переменных ü целевую функцию. Математически общую модель задачи можно представить в виде: Найти значения n переменных
Максимизирует или минимизирует целевую функцию
Если на переменные налагается условие неотрицательности, тогда в модель задачи вводится условие Если ограничения и целевая функция линейны относительно переменных, то модель называют линейной. А в случае, если хотя бы одна из функций fi или F нелинейна, то модель называют нелинейной. Рассмотрим примеррешения задачи методом линейного программирования (ЗЛП). Рыборазводное предприятие решает заселить водоем двумя видами рыб А и В. Средняя масса рыбы равна 2 кг для вида А и 1 кг для вида В. В озере имеется два вида пищи: Р1 и Р2. Средние потребности одной рыбы вида А составляют 1 ед. корма Р1 и 3 ед. корма Р2 в день. Аналогичные потребности для рыбы вида В составляют 2 ед. Р1 и 1 ед. Р2. Ежедневный запас пищи поддерживается на уровне 500 ед. Р1 и 900 ед. Р2. Условие данной задачи можно представить в виде таблицы 3.1 Таблица 3.1 Исходные данные к задаче
Как следует заселить озеро рыбами, чтобы максимизировать общую массу рыб? Решить задачу можно множеством способов, в том числе: графическим, симплекс – методом, способом подстановки. Рассмотрим графический метод.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.006 с.) |
 , меньше или равно
, меньше или равно  ;
; ;
;
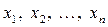 , которые удовлетворяют системе ограничений
, которые удовлетворяют системе ограничений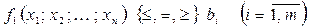 ;
; .
. .
.


