
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особливості розрахунку статично невизначних двошарнірних арокСодержание книги
Поиск на нашем сайте
Різновиди статично невизначних арок. Вибір розрахункової схеми і методу розрахунку. Особливості розрахунку двохшарнірних та безшарнірних арок. Вплив обтиснення на арку (двохшарнірні арки із затяжкою). Поняття про регулювання напружень в арках. Методичні вказівки Вивчаючи цю тему, в першу чергу необхідно звернути увагу на класифікацію арок, вибір основної системи. При розрахунках статично невизначних арок, як правило, використовують метод сил. Особливістю розрахунку арок є врахування при обчисленні переміщень криволінійності осі арки та можливої зміни її жорсткостей у межах прольоту, а також необхідність урахування поперечних і поздовжніх зусиль. Для спрощення розрахунків інколи замінюють криволінійну вісь арки окремими прямолінійними ділянками, кінці яких розташовані на її осі. Для статично невизначних арок із затяжкою необхідно проаналізувати вплив податливості затяжки на значення внутрішніх зусиль арки, а також можливість їх зміни шляхом регулювання зусилля у затяжці. При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою Ø при співвідношенні висоти перерізу арки до її прольоту ( Ø коли Канонічне рівняння методу сил записується так: де
Значення
де
При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку, коли можна скористатися спрощеннями, що вказані вище, значення
Для арки без затяжки Значення
де
При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку, коли можна скористатися спрощеннями, що вказані вище, значення
Після визначення з канонічного рівняння невідомого
Для арки без затяжки розпір Питання та завдання для самоконтролю 1 Як підрахувати ступінь статичної невизначності системи? 2 В чому полягає ідея методу сил? Основні невідомі методу сил. 3 Що таке основна система методу сил і способи її утворення? 4 Які фактори впливають на вибір раціональної основної системи? 5 Зміст канонічних рівнянь і окремих їх елементів при розрахунку балок, рам, арок та ферм. 6 Які спрощення використовуються при обчисленні коефіцієнтів матриці податливості та вектора вільних членів у розрахунках різних типів стрижневих систем? 7 Як виконується перевірка коефіцієнтів матриці податливості та вектора вільних членів канонічних рівнянь? 8 Як будуються епюри внутрішніх зусиль для різних типів стрижневих систем? 9 Виконання перевірок епюр внутрішніх зусиль. 10 Урахування симетрії системи. 11 Використання групових невідомих. 12 Особливості розрахунку статично невизначних ферм. 13 Особливості розрахунку статично невизначних арок. 14 Особливості обчислення переміщень у статично невизначних системах. 15 Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор. 16 Сформулюйте пункти алгоритму розрахунку СНС методом сил. Метод переміщень Література: /1/ с.319-441; /2/ с.265-302; /3/ с.372-386, 389-390, 397-402; /4/ с.135-150, 152-155; /5/ с.194-216.
Основні поняття та ключові слова розділу: ступінь кінематичної невизначності системи, основна система та основні невідомі, канонічні рівняння, матриця жорсткості, вектор вільних членів. Ступінь кінематичної невизначності плоских систем. Ідея методу переміщень. Невідомі методу переміщень. Основна система методу переміщень. Канонічні рівняння. Обчислення і перевірка коефіцієнтів та вільних членів канонічних рівнянь. Матриця жорсткості системи й вектор вільних членів канонічних рівнянь. Побудова епюр внутрішніх зусиль (М, Q, N) та їх перевірка. Загальний алгоритм розрахунку статично невизначних систем методом переміщень. Урахування симетрії. Матрична форма методу переміщень. Розрахунок на зміну температури і переміщення опор. Методичні вказівки Метод переміщень є одним із основних для розрахунку СНС. Його засвоєння необхідне для розрахунків конструкцій, будівель і споруд та успішного вивчення інших тем курсу. Він покладений в основу методу скінченних елементів. Важливо навчитися визначати кількість невідомих методу переміщень (ступінь кінематичної невизначності системи). Деформований стан плоскої стрижньової системи може бути одержаний за допомогою обмеженої кількості параметрів. Такими параметрами є кути повороту жорстких вузлів системи (nв) та лінійні переміщення її вузлів (nл). Кількість кутів повороту дорівнює кількості жорстких вузлів системи, а кількість лінійних переміщень – кількості ступенів свободи умовної шарнірно-стрижньової системи, яка утворюється шляхом розташування шарнірів у всіх жорстких вузлах заданої системи, включаючи й опорні защемлення. Таким чином, ступінь кінематичної невизначності системи (n) дорівнює – n = nв + nл . За основні невідомі методу переміщень приймають кутові переміщення жорстких вузлів і лінійні переміщення вузлів заданої системи, які звичайно позначають Важливо засвоїти зміст коефіцієнтів та вільних членів канонічних рівнянь методу переміщень і звернути увагу на їх знаки й виконання умови
Рівняння методу переміщень можна складати у двох формах: канонічній або розгорнутій (у формі основних і додаткових рівнянь). Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою статичного методу або шляхом перемноження епюр. При складанні рівнянь у розгорнутій формі використовуються формули для значень реакцій у кінцевих перерізах окремих стрижнів основної системи від кінематичних, силових й інших впливів (див. додатки А і Б). При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням умови При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження вільних членів канонічних рівнянь. Епюри внутрішніх зусиль для заданої статично невизначної системи при використанні канонічної форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження та інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою
де
n – ступінь кінематичної невизначності системи. Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом: 1. За допомогою формули (2) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи. 2. У подальшому виконуються пункти алгоритму (2 і 3), які вказані в алгоритмі для методу сил. Після побудови епюр внутрішніх зусиль, необхідно виконати їх статичну й кінематичну перевірки. Епюри внутрішніх зусиль (M, Q і N) для заданої системи при використанні розгорнутої форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів за таким алгоритмом: 1. Значення згинальних моментів та поперечних сил у кінцевих перерізах окремих стрижнів від основних невідомих (φ і δ), зовнішнього навантаження й інших впливів визначаються з використанням формул, указаних у додатках А і Б.
2. У подальшому виконується пункт 2 алгоритму, який указаний в алгоритмі для канонічної форми методу переміщень. При розрахунках рам із використанням обчислювальної техніки зручною буде матрична форма методу переміщень. Питання та завдання для самоконтролю 1 Як підрахувати ступінь кінематичної невизначності системи? 2 В чому полягає ідея методу переміщень? Основні невідомі методу переміщень. 3 Що таке основна система методу переміщень та її утворення? 4 Канонічна та розгорнута форма рівнянь методу переміщень. 5 Зміст канонічних рівнянь і окремих їх елементів. 6 Як обчислюються коефіцієнти матриці жорсткості та вектора вільних членів? 7 Як виконується перевірка коефіцієнтів матриці жорсткості і вектора вільних членів канонічних рівнянь? 8 Як будуються епюри внутрішніх зусиль при використанні канонічної та розгорнутої форм методу переміщень? 9 Виконання перевірок епюр внутрішніх зусиль. 10 Урахування симетрії системи. 11 Використання групових невідомих. 12 Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор. 13 Сформулюйте пункти алгоритму розрахунку СНС методом переміщень. ЛІТЕРАТУРА Основна 1 Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. - М.: Стройиздат, 1981. - 512 с. 2 Дарков А.В., Шапошников Н.Н. Строительная механика. - 8-е изд., перераб. и доп. – М.: Высш. школа, 1986. – 544 с. 3 Киселев В.А. Строительная механика, общий курс – 4-е изд., исправленное и доп. – М.: Стройиздат, 1986. – 520 с. 4 Бутенко Ю.И., Кан С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. - К.: Вища школа, 1980. - 488 с. 5 Доценко И.С. Строительная механика. – К.: Вища школа, 1976. - 296 с. Допоміжна 6 Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. - К.: Вища школа, 1989. - 367 с. 8 Ржаницин А.Р. Строительная механика. - М.: Высшая школа, 1982. - 400 с. (2-е изд., перераб. и доп., 1991. - 439 с.) 9 Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. - 3-е изд., перераб. и доп. - М.: Высшая школа, 1973. - 360 с. Додаток А
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.12.30 (3.59 с.) |

 , з початком координат на будь-якій із шарнірних опор, де
, з початком координат на будь-якій із шарнірних опор, де  – стріла підйому арки;
– стріла підйому арки;  – проліт арки, можна використати такі спрощення:
– проліт арки, можна використати такі спрощення: ), а також
), а також  нехтують поперечними та поздовжніми силами при обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил;
нехтують поперечними та поздовжніми силами при обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил; , тоді інтегрування за довжиною дуги арки, при обчисленні коефіцієнта та вільного члена канонічного рівняння методу сил, замінюється інтегруванням за горизонтальною проекцією осі арки (
, тоді інтегрування за довжиною дуги арки, при обчисленні коефіцієнта та вільного члена канонічного рівняння методу сил, замінюється інтегруванням за горизонтальною проекцією осі арки (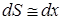 ).
). ,
, – основне невідоме методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це зусилля в затяжці);
– основне невідоме методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це зусилля в затяжці); – переміщення перерізу, де прикладена (прикладені)
– переміщення перерізу, де прикладена (прикладені) 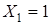 ;
; – переміщення перерізу, де прикладена (прикладені)
– переміщення перерізу, де прикладена (прикладені)  ,
, – внутрішні зусилля в арці та затяжці від
– внутрішні зусилля в арці та затяжці від  – коефіцієнт, що враховує форму поперечного перерізу арки;
– коефіцієнт, що враховує форму поперечного перерізу арки; – відповідні жорсткості арки та затяжки.
– відповідні жорсткості арки та затяжки.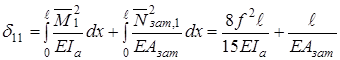 .
. .
. ,
, – внутрішні зусилля в арці від
– внутрішні зусилля в арці від  – внутрішні зусилля в арці від зовнішнього навантаження або інших впливів.
– внутрішні зусилля в арці від зовнішнього навантаження або інших впливів. .
. .
. .
. . Кількість невідомих дорівнює ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна система, яка утворюється із заданої системи “накладанням” у вузлах в’язей, що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу переміщень являє собою сукупність взаємозв’язаних стрижнів із різними закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для основної системи можна записати умови її еквівалентності заданій системі на основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних в’язях при усуненні відмінності основної системи від заданої). Деяка і -та умова еквівалентності відображає те, що сума реакцій в і -тій фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших впливів дорівнює нулю. При цьому використовують принцип незалежності дій та закон Гука. Як правило, умови еквівалентності записують в канонічній формі і називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі – переміщення вузлів заданої системи.
. Кількість невідомих дорівнює ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна система, яка утворюється із заданої системи “накладанням” у вузлах в’язей, що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу переміщень являє собою сукупність взаємозв’язаних стрижнів із різними закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для основної системи можна записати умови її еквівалентності заданій системі на основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних в’язях при усуненні відмінності основної системи від заданої). Деяка і -та умова еквівалентності відображає те, що сума реакцій в і -тій фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших впливів дорівнює нулю. При цьому використовують принцип незалежності дій та закон Гука. Як правило, умови еквівалентності записують в канонічній формі і називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі – переміщення вузлів заданої системи. , згідно з теоремою про взаємність реакцій. Основна система у методі переміщень, на відміну від методу сил, завжди вибирається, як правило, однозначно: у жорстких вузлах системи накладають в’язі, які перешкоджають кутовим переміщенням, але не перешкоджають лінійним, а у вузлах, що мають лінійні переміщення, накладають в’язі, які перешкоджають лінійним переміщенням, але не перешкоджають кутовим.
, згідно з теоремою про взаємність реакцій. Основна система у методі переміщень, на відміну від методу сил, завжди вибирається, як правило, однозначно: у жорстких вузлах системи накладають в’язі, які перешкоджають кутовим переміщенням, але не перешкоджають лінійним, а у вузлах, що мають лінійні переміщення, накладають в’язі, які перешкоджають лінійним переміщенням, але не перешкоджають кутовим. (2)
(2) – епюра згинальних моментів в основній системі від
– епюра згинальних моментів в основній системі від 
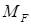 – епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;
– епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;


