
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра опору матеріалів і будівельної механікиСодержание книги Поиск на нашем сайте
БУДІВЕЛЬНИЙ ФАКУЛЬТЕТ Кафедра опору матеріалів і будівельної механіки
Методичні вказівки та контрольні завдання з дисципліни “ Будівельна механіка (спецкурс) ” для студентів денної форми навчання Частина 2 (статично невизначні системи)
Полтава 2003 Методичні вказівки та контрольні завдання з дисципліни “Будівельна механіка (спецкурс)” для студентів денної форми навчання. Частина 2 (статично невизначні системи).– Полтава: Полт НТУ, 2003.– 29 с.
Укладачі: О.А.Шкурупій, кандидат технічних наук, доцент; Б.П.Митрофанов, кандидат технічних наук, доцент; А.М.Пащенко, старший викладач.
Відповідальний за випуск - завідувач кафедри опору матеріалів і будівельної механіки О.В.Горик, кандидат технічних наук, професор.
Рецензент: доктор технічних наук, професор, завідувач кафедри конструкцій із металу, дерева та пластмас С.Ф.Пічугін
Затверджено на засіданні ради університету протокол № 11 від 30.05.2003 р.
Літературний редактор Н.В.Жигилій Коректор Н.О.Янкевич
ЗМІСТ
ЗАГАЛЬНІ ВКАЗІВКИ.. 4 СТАТИЧНО НЕВИЗНАЧНІ СТРИЖНЬОВІ СИСТЕМИ.. 5 1. Статично невизначні системи і їх ознаки. 5 2. Метод сил. 5 2.1 Особливості розрахунку статично невизначних двошарнірних арок. 7 3. Метод переміщень. 10 ЛІТЕРАТУРА.. 13 Додаток А.. 14 Формули для розрахунку стрижневих систем на міцність методом переміщень у розгорнутій формі 14 Додаток Б. 15 Моменти і поперечні сили на кінцях окремих елементів основної системи методу переміщень від зовнішнього навантаження та температурних впливів. 15 Додаток В.. 16 Таблиці вихідних даних для виконання РГР. 16 Додаток Г. 18 Розрахункові схеми рам для РГР №1. 18 Додаток Д.. 22 Розрахункові схеми арок для РГР №2. 22 Додаток Е. 24 Розрахункові схеми рам для РГР №3. 24 Додаток Ж.. 28 Екзаменаційні питання з курсу “Будівельна механіка” (спецкурс) 28
ЗАГАЛЬНІ ВКАЗІВКИ Методичні вказівки розроблені відповідно до навчальної програми з дисципліни “Будівельна механіка (спецкурс)” (напрям підготовки 0921 – “Будівництво”) для студентів будівельних спеціальностей: "Промислове і цивільне будівництво" (спеціалізації “Сільськогосподарське будівництво”, “Проектування і спорудження об’єктів нафтогазодобувного комплексу”); “Міське будівництво та господарство” й ін. Основна форма вивчення курсу будівельної механіки для студентів – це самостійна робота з навчально-методичною літературою і виконання розрахунково-графічних робіт (у подальшому РГР). Вивчення цього спецкурсу будівельної механіки потрібно розпочинати із засвоєння теоретичного матеріалу у підручниках, навчальних посібниках. Після цього рекомендується розпочати розв’язання задач, які наведені у підручниках та посібниках, а потім виконувати індивідуальні завдання (РГР №1, №2, №3). Основні розділи спецкурсу будівельної механіки викладаються студентам на лекціях і практичних заняттях, на яких роз’яснюються та доповнюються основні положення. Дані для виконання РГР №1, №2, №3 вибираються студентом із таблиць за шифром. Шифр варіанта складається із трьох цифр і визначається згідно з номером залікової книжки студента. Першу цифру шифру визначають як останню із суми всіх цифр номера залікової книжки студента. Наприклад, номер залікової книжки студента - 21486. Тоді сума всіх цифр буде дорівнювати 2+1+4+8+6=21. Таким чином, перша цифра шифру буде дорівнювати 1. Другу цифру шифру визначають як останню із суми всіх цифр номера залікової книжки студента без урахування першої. Тоді сума цих цифр буде дорівнювати 1+4+8+6=19. Отже, друга цифра шифру - 9. Третю цифру шифру визначають як останню з усіх цифр номера залікової книжки студента. Наприклад, номер залікової книжки студента - 21486. Тоді третя цифра шифру буде 6. Остаточний шифр варіанта, згідно з номером залікової книжки 21486, буде 196. Значення вихідних даних для розрахунку відповідних частин курсової роботи (геометричних розмірів, навантажень тощо) необхідно брати з таблиць у рядках 1, 9 і 6. Номер розрахункової схеми для всіх завдань визначається двома останніми цифрами номера залікової книжки. Якщо число, яке визначене двома останніми цифрами номера залікової книжки, більше ніж 30 або 60, або 90, тоді для визначення номера розрахункової схеми необхідно відняти від нього відповідно 30 або 60, або 90. Наприклад, номер залікової книжки студента - 21486. Тоді номер розрахункової схеми буде дорівнювати 86-60 = 26. Розрахунково-графічні роботи виконуються відповідно до Положення про виконання курсових проектів та робіт Полтавського національного технічного університету імені Юрія Кондратюка і виданого завдання. Всі рисунки необхідно виконувати з дотриманням лінійних та силових масштабів на аркушах формату А4. На епюрах необхідно вказувати характерні значення ординат, а в масштабах указати їх розмірність. Метод сил Література: /1/ с.316-349, 361-368; /2/ 198-231, 238-249; /3/ с.238-258; /4/ с.102-131; /5/ с.132-135, 154-191. Основні поняття та ключові слова розділу: ступінь статичної невизначності системи, основна система та основні невідомі, канонічні рівняння, матриця податливості, вектор вільних членів, ортогональні епюри. Ступінь статичної невизначності плоских систем. Сутність методу сил. Основна система методу сил. Канонічні рівняння. Обчислення і перевірка коефіцієнтів та вільних членів канонічних рівнянь. Матриця податливості системи й вектор вільних членів канонічних рівнянь. Ортогоналізація епюр. Побудова епюр внутрішніх зусиль (М, Q, N) та їх перевірка. Загальний алгоритм розрахунку статично невизначних систем методом сил. Визначення переміщень у статично невизначних системах. Урахування симетрії. Матрична форма методу сил. Розрахунок СНС на зміну температури та переміщення опор. Методичні вказівки Метод сил є одним із основних для розрахунку СНС. Його засвоєння необхідне при подальшому проектуванні конструкцій, будівель і споруд та успішного вивчення інших тем курсу. Важливо навчитися визначати кількість невідомих методу сил (ступінь статичної невизначності системи). У методі сил використовується система, яка називається основною системою. Вона отримується із заданої системи шляхом відкидання умовно зайвих в’язей і навантаження її зовнішніми силами та зусиллями відкинутих зайвих в’язей. Ці зусилля називають основними невідомими методу сил, які зазвичай позначають Важливо засвоїти сутність коефіцієнтів і вільних членів канонічних рівнянь методу сил і звернути увагу на їх знаки та виконання умови Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою методу Мора. При цьому інтеграли Мора можна вираховувати відповідно до правила Верещагіна або за формулою Сімпсона-Корноухова. При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням сумарної епюри внутрішніх зусиль від одиничних навантажень. Для симетричних систем значних спрощень можна досягти, враховуючи їх симетрію. При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження вільних членів канонічних рівнянь. Епюри внутрішніх зусиль для заданої статично невизначної системи будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою
де
Л – ступінь статичної невизначності системи. Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом: 1. За допомогою формули (1) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи. 2. Кожен стрижень системи розглядаємо як балку з шарнірними опорами в кінцевих перерізах, для якої будуються епюри M і Q від зовнішнього навантаження стрижня та моментів, що обчислені в пункті 1. Об’єднавши відповідні епюри M і Q стрижнів системи, отримуємо епюри M і Q для заданої системи. 3. Епюру поздовжніх зусиль (N) будуємо шляхом використання умов рівноваги окремих вузлів системи. Після побудови епюр внутрішніх зусиль необхідно виконати їх статичну й кінематичну перевірки. Знаходження переміщень у статично невизначних системах виконується так, як і в статично визначних, із використанням методу Мора. Наприклад, у балках та рамах переміщення, пов’язане зі згином, обчислюється за формулою
де
Використання обчислювальної техніки зменшує трудомісткість розрахунку статично невизначних систем методом сил. При цьому найбільш раціональною є матрична форма розв’язання задачі. Методичні вказівки Вивчаючи цю тему, в першу чергу необхідно звернути увагу на класифікацію арок, вибір основної системи. При розрахунках статично невизначних арок, як правило, використовують метод сил. Особливістю розрахунку арок є врахування при обчисленні переміщень криволінійності осі арки та можливої зміни її жорсткостей у межах прольоту, а також необхідність урахування поперечних і поздовжніх зусиль. Для спрощення розрахунків інколи замінюють криволінійну вісь арки окремими прямолінійними ділянками, кінці яких розташовані на її осі. Для статично невизначних арок із затяжкою необхідно проаналізувати вплив податливості затяжки на значення внутрішніх зусиль арки, а також можливість їх зміни шляхом регулювання зусилля у затяжці. При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою Ø при співвідношенні висоти перерізу арки до її прольоту ( Ø коли Канонічне рівняння методу сил записується так: де
Значення
де
При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку, коли можна скористатися спрощеннями, що вказані вище, значення
Для арки без затяжки Значення
де
При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку, коли можна скористатися спрощеннями, що вказані вище, значення
Після визначення з канонічного рівняння невідомого
Для арки без затяжки розпір Питання та завдання для самоконтролю 1 Як підрахувати ступінь статичної невизначності системи? 2 В чому полягає ідея методу сил? Основні невідомі методу сил. 3 Що таке основна система методу сил і способи її утворення? 4 Які фактори впливають на вибір раціональної основної системи? 5 Зміст канонічних рівнянь і окремих їх елементів при розрахунку балок, рам, арок та ферм. 6 Які спрощення використовуються при обчисленні коефіцієнтів матриці податливості та вектора вільних членів у розрахунках різних типів стрижневих систем? 7 Як виконується перевірка коефіцієнтів матриці податливості та вектора вільних членів канонічних рівнянь? 8 Як будуються епюри внутрішніх зусиль для різних типів стрижневих систем? 9 Виконання перевірок епюр внутрішніх зусиль. 10 Урахування симетрії системи. 11 Використання групових невідомих. 12 Особливості розрахунку статично невизначних ферм. 13 Особливості розрахунку статично невизначних арок. 14 Особливості обчислення переміщень у статично невизначних системах. 15 Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор. 16 Сформулюйте пункти алгоритму розрахунку СНС методом сил. Метод переміщень Література: /1/ с.319-441; /2/ с.265-302; /3/ с.372-386, 389-390, 397-402; /4/ с.135-150, 152-155; /5/ с.194-216. Основні поняття та ключові слова розділу: ступінь кінематичної невизначності системи, основна система та основні невідомі, канонічні рівняння, матриця жорсткості, вектор вільних членів. Ступінь кінематичної невизначності плоских систем. Ідея методу переміщень. Невідомі методу переміщень. Основна система методу переміщень. Канонічні рівняння. Обчислення і перевірка коефіцієнтів та вільних членів канонічних рівнянь. Матриця жорсткості системи й вектор вільних членів канонічних рівнянь. Побудова епюр внутрішніх зусиль (М, Q, N) та їх перевірка. Загальний алгоритм розрахунку статично невизначних систем методом переміщень. Урахування симетрії. Матрична форма методу переміщень. Розрахунок на зміну температури і переміщення опор. Методичні вказівки Метод переміщень є одним із основних для розрахунку СНС. Його засвоєння необхідне для розрахунків конструкцій, будівель і споруд та успішного вивчення інших тем курсу. Він покладений в основу методу скінченних елементів. Важливо навчитися визначати кількість невідомих методу переміщень (ступінь кінематичної невизначності системи). Деформований стан плоскої стрижньової системи може бути одержаний за допомогою обмеженої кількості параметрів. Такими параметрами є кути повороту жорстких вузлів системи (nв) та лінійні переміщення її вузлів (nл). Кількість кутів повороту дорівнює кількості жорстких вузлів системи, а кількість лінійних переміщень – кількості ступенів свободи умовної шарнірно-стрижньової системи, яка утворюється шляхом розташування шарнірів у всіх жорстких вузлах заданої системи, включаючи й опорні защемлення. Таким чином, ступінь кінематичної невизначності системи (n) дорівнює – n = nв + nл . За основні невідомі методу переміщень приймають кутові переміщення жорстких вузлів і лінійні переміщення вузлів заданої системи, які звичайно позначають Важливо засвоїти зміст коефіцієнтів та вільних членів канонічних рівнянь методу переміщень і звернути увагу на їх знаки й виконання умови Рівняння методу переміщень можна складати у двох формах: канонічній або розгорнутій (у формі основних і додаткових рівнянь). Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою статичного методу або шляхом перемноження епюр. При складанні рівнянь у розгорнутій формі використовуються формули для значень реакцій у кінцевих перерізах окремих стрижнів основної системи від кінематичних, силових й інших впливів (див. додатки А і Б). При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням умови При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження вільних членів канонічних рівнянь. Епюри внутрішніх зусиль для заданої статично невизначної системи при використанні канонічної форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження та інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою
де
n – ступінь кінематичної невизначності системи. Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом: 1. За допомогою формули (2) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи. 2. У подальшому виконуються пункти алгоритму (2 і 3), які вказані в алгоритмі для методу сил. Після побудови епюр внутрішніх зусиль, необхідно виконати їх статичну й кінематичну перевірки. Епюри внутрішніх зусиль (M, Q і N) для заданої системи при використанні розгорнутої форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів за таким алгоритмом: 1. Значення згинальних моментів та поперечних сил у кінцевих перерізах окремих стрижнів від основних невідомих (φ і δ), зовнішнього навантаження й інших впливів визначаються з використанням формул, указаних у додатках А і Б. 2. У подальшому виконується пункт 2 алгоритму, який указаний в алгоритмі для канонічної форми методу переміщень. При розрахунках рам із використанням обчислювальної техніки зручною буде матрична форма методу переміщень. Питання та завдання для самоконтролю 1 Як підрахувати ступінь кінематичної невизначності системи? 2 В чому полягає ідея методу переміщень? Основні невідомі методу переміщень. 3 Що таке основна система методу переміщень та її утворення? 4 Канонічна та розгорнута форма рівнянь методу переміщень. 5 Зміст канонічних рівнянь і окремих їх елементів. 6 Як обчислюються коефіцієнти матриці жорсткості та вектора вільних членів? 7 Як виконується перевірка коефіцієнтів матриці жорсткості і вектора вільних членів канонічних рівнянь? 8 Як будуються епюри внутрішніх зусиль при використанні канонічної та розгорнутої форм методу переміщень? 9 Виконання перевірок епюр внутрішніх зусиль. 10 Урахування симетрії системи. 11 Використання групових невідомих. 12 Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор. 13 Сформулюйте пункти алгоритму розрахунку СНС методом переміщень. ЛІТЕРАТУРА Основна 1 Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. - М.: Стройиздат, 1981. - 512 с. 2 Дарков А.В., Шапошников Н.Н. Строительная механика. - 8-е изд., перераб. и доп. – М.: Высш. школа, 1986. – 544 с. 3 Киселев В.А. Строительная механика, общий курс – 4-е изд., исправленное и доп. – М.: Стройиздат, 1986. – 520 с. 4 Бутенко Ю.И., Кан С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. - К.: Вища школа, 1980. - 488 с. 5 Доценко И.С. Строительная механика. – К.: Вища школа, 1976. - 296 с. Допоміжна 6 Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. - К.: Вища школа, 1989. - 367 с. 8 Ржаницин А.Р. Строительная механика. - М.: Высшая школа, 1982. - 400 с. (2-е изд., перераб. и доп., 1991. - 439 с.) 9 Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. - 3-е изд., перераб. и доп. - М.: Высшая школа, 1973. - 360 с. Додаток А Додаток Б Закінчення додатка Б
Додаток В Таблиця 1 – Вихідні дані для РГР№1
Закінчення додатка В Таблиця 2 – Вихідні дані для РГР№2
Примітка: Окреслення осі арки по квадратній параболі: Таблиця 3 – Вихідні дані для РГР№3
Примітка: В елементах розрахункових схем, які позначені товстою лінією, відповідні згинальні жорсткості необхідно збільшувати у три рази.
Додаток Г Додаток Д Додаток Е Додаток Ж Екзаменаційні питання з курсу “Будівельна механіка” (спецкурс) 1. На прикладі нерозрізної балки з двома зайвими в’язями розкрийте суть одного з канонічних рівнянь методу сил та його розмірність. Укажіть розмірність усіх членів цього рівняння. 2. В чому суть головних коефіцієнтів канонічних рівнянь методу сил, складених для нерозрізної балки з двома зайвими в'язями? Відповідь проілюструйте, запишіть рівняння. 3. У чому суть побічних коефіцієнтів канонічних рівнянь методу сил, складених для балки з двома зайвими в'язями, одна з котрих лінійна, а друга – кутова? Відповідь проілюструйте, запишіть рівняння. 4. Для балки із защемленими кінцями виведіть формулу згинального моменту біля правої опори від повороту лівого затиснення. 5. В чому суть головних коефіцієнтів рівнянь методу переміщень, складених для рами з трьома невідомими, з яких одне лінійне? Відповідь проілюструйте. 6. Обґрунтуйте перевірку коефіцієнтів третього канонічного рівняння методу сил, складеного для рами з чотирма зайвими в'язями. Відповідь проілюструйте. 7. Обґрунтуйте перевірку вільних членів канонічних рівнянь методу сил, складених для рами з чотирма зайвими в'язями. Відповідь проілюструйте. 8. Складіть і обґрунтуйте вираз головного коефіцієнта канонічного рівняння методу сил для точного розрахунку арки з однією зайвою в'яззю. 9. Для балки з одним шарнірним, а другим защемленим кінцем виведіть формулу згинального моменту біля затиснення від лінійного зміщення опори. 10. На прикладі ферми з двома зайвими в'язями розкрийте суть одного з канонічних рівнянь методу сил та його розмірність. Укажіть розмірність усіх членів цього рівняння. Відповідь проілюструйте. 11. На прикладі рами з двома зайвими в'язями обґрунтуйте раціональний спосіб визначення переміщень у статично невизначній системі. 12. У чому полягає суть кінематичної перевірки рішення статично невизначної системи? Обґрунтуйте на прикладі рами з однією зайвою в'яззю. 13. Для балки з одним шарнірним, а другим защемленим кінцем виведіть формулу згинального моменту біля затиснення від повороту цього защемлення. 14. У чому суть рівняння для визначення розпору в двошарнірній арці без затяжки? Що являють собою всі члени рівняння? Відповідь проілюструйте. 15. Для балки з одним шарнірним, а другим защемленим кінцем виведіть формулу поперечної сили від повороту защемлення. 16. Проаналізуйте основну систему змішаного методу, побудовану для рами з двома невідомими. Зіставте її з основними системами методу сил та методу переміщень для тієї ж схеми. Відповідь проілюструйте. 17. У чому суть побічних коефіцієнтів канонічних рівнянь змішаного методу, складених для рами з двома невідомими? Проілюструйте відповідь, запишіть рівняння. 18. Для балки зі защемленими кінцями виведіть формулу поперечної сили від повороту одного із защемлень. 19. У чому суть побічних коефіцієнтів у другому рівнянні методу переміщень, складених для рами з трьома невідомими, з яких одне лінійне? Проілюструйте відповідь, запишіть рівняння. 20. Для балки зі защемленими кінцями виведіть формулу поперечної сили, яка викликана лінійним зміщенням однієї з опор. 21. У чому суть кінематичної перевірки рішення статично невизначної системи? Обґрунтуйте на прикладі балки з двома зайвими в’язями. 22
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |



 . Для основної системи методу сил можна записати умови її еквівалентності заданій системі у формі рівнянь нерозривності переміщень у перерізах, де відкинуті зайві в’язі. Деяка і -та умова еквівалентності відображає те, що переміщення перерізу (перерізів), де прикладена і -та основна невідома в напрямку її дії від основних невідомих, зовнішнього навантаження й інших впливів, дорівнює нулю. Як правило, умови еквівалентності записують у канонічній формі і називаються канонічними рівняннями методу сил. Кількість канонічних рівнянь, як правило, дорівнює ступеню статичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі.
. Для основної системи методу сил можна записати умови її еквівалентності заданій системі у формі рівнянь нерозривності переміщень у перерізах, де відкинуті зайві в’язі. Деяка і -та умова еквівалентності відображає те, що переміщення перерізу (перерізів), де прикладена і -та основна невідома в напрямку її дії від основних невідомих, зовнішнього навантаження й інших впливів, дорівнює нулю. Як правило, умови еквівалентності записують у канонічній формі і називаються канонічними рівняннями методу сил. Кількість канонічних рівнянь, як правило, дорівнює ступеню статичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі.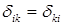 , згідно з теоремою про взаємність переміщень. Основна система повинна бути вибрана таким чином, щоб епюри внутрішніх зусиль від одиничних і зовнішніх навантажень були якомога простими й взаємно ортогональними. При цьому рекомендується розглянути декілька варіантів основних систем і, порівнюючи їх, вибрати раціональну.
, згідно з теоремою про взаємність переміщень. Основна система повинна бути вибрана таким чином, щоб епюри внутрішніх зусиль від одиничних і зовнішніх навантажень були якомога простими й взаємно ортогональними. При цьому рекомендується розглянути декілька варіантів основних систем і, порівнюючи їх, вибрати раціональну.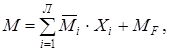 (1)
(1) – епюра згинальних моментів в основній системі від
– епюра згинальних моментів в основній системі від 
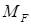 – епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;
– епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;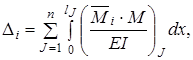
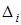 – будь-яке лінійне або кутове переміщення;
– будь-яке лінійне або кутове переміщення;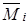 – функція згинального моменту, яка складена для j -ї ділянки інтегрування у допоміжному (одиничному) стані будь-якоїосновної системи методу сил;
– функція згинального моменту, яка складена для j -ї ділянки інтегрування у допоміжному (одиничному) стані будь-якоїосновної системи методу сил;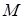 – функція згинального моменту, яка складена для j -ї ділянки інтегрування у заданій статично невизначній системі.
– функція згинального моменту, яка складена для j -ї ділянки інтегрування у заданій статично невизначній системі. , з початком координат на будь-якій із шарнірних опор, де
, з початком координат на будь-якій із шарнірних опор, де  – стріла підйому арки;
– стріла підйому арки;  – проліт арки, можна використати такі спрощення:
– проліт арки, можна використати такі спрощення: ), а також
), а також  нехтують поперечними та поздовжніми силами при обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил;
нехтують поперечними та поздовжніми силами при обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил; , тоді інтегрування за довжиною дуги арки, при обчисленні коефіцієнта та вільного члена канонічного рівняння методу сил, замінюється інтегруванням за горизонтальною проекцією осі арки (
, тоді інтегрування за довжиною дуги арки, при обчисленні коефіцієнта та вільного члена канонічного рівняння методу сил, замінюється інтегруванням за горизонтальною проекцією осі арки (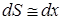 ).
). ,
, – основне невідоме методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це зусилля в затяжці);
– основне невідоме методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це зусилля в затяжці); – переміщення перерізу, де прикладена (прикладені)
– переміщення перерізу, де прикладена (прикладені) 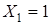 ;
; – переміщення перерізу, де прикладена (прикладені)
– переміщення перерізу, де прикладена (прикладені)  ,
, – внутрішні зусилля в арці та затяжці від
– внутрішні зусилля в арці та затяжці від  – коефіцієнт, що враховує форму поперечного перерізу арки;
– коефіцієнт, що враховує форму поперечного перерізу арки; – відповідні жорсткості арки та затяжки.
– відповідні жорсткості арки та затяжки.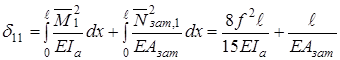 .
. .
. ,
, – внутрішні зусилля в арці від
– внутрішні зусилля в арці від  – внутрішні зусилля в арці від зовнішнього навантаження або інших впливів.
– внутрішні зусилля в арці від зовнішнього навантаження або інших впливів. .
. .
. .
. . Кількість невідомих дорівнює ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна система, яка утворюється із заданої системи “накладанням” у вузлах в’язей, що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу переміщень являє собою сукупність взаємозв’язаних стрижнів із різними закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для основної системи можна записати умови її еквівалентності заданій системі на основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних в’язях при усуненні відмінності основної системи від заданої). Деяка і -та умова еквівалентності відображає те, що сума реакцій в і -тій фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших впливів дорівнює нулю. При цьому використовують принцип незалежності дій та закон Гука. Як правило, умови еквівалентності записують в канонічній формі і називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі – переміщення вузлів заданої системи.
. Кількість невідомих дорівнює ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна система, яка утворюється із заданої системи “накладанням” у вузлах в’язей, що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу переміщень являє собою сукупність взаємозв’язаних стрижнів із різними закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для основної системи можна записати умови її еквівалентності заданій системі на основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних в’язях при усуненні відмінності основної системи від заданої). Деяка і -та умова еквівалентності відображає те, що сума реакцій в і -тій фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших впливів дорівнює нулю. При цьому використовують принцип незалежності дій та закон Гука. Як правило, умови еквівалентності записують в канонічній формі і називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі – переміщення вузлів заданої системи. , згідно з теоремою про взаємність реакцій. Основна система у методі переміщень, на відміну від методу сил, завжди вибирається, як правило, однозначно: у жорстких вузлах системи накладають в’язі, які перешкоджають кутовим переміщенням, але не перешкоджають лінійним, а у вузлах, що мають лінійні переміщення, накладають в’язі, які перешкоджають лінійним переміщенням, але не перешкоджають кутовим.
, згідно з теоремою про взаємність реакцій. Основна система у методі переміщень, на відміну від методу сил, завжди вибирається, як правило, однозначно: у жорстких вузлах системи накладають в’язі, які перешкоджають кутовим переміщенням, але не перешкоджають лінійним, а у вузлах, що мають лінійні переміщення, накладають в’язі, які перешкоджають лінійним переміщенням, але не перешкоджають кутовим. (2)
(2)

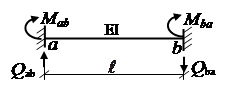


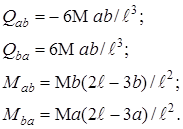



 – температурний коефіцієнт лінійного розширення;
h – висота перерізу;
– температурний коефіцієнт лінійного розширення;
h – висота перерізу;  t = (
t = ( )>0.
)>0.

 .
.


