
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статично невизначні стрижньові системиСодержание книги Поиск на нашем сайте
ПРОГРАМА ТА МЕТОДИЧНІ ВКАЗІВКИ ДО ТЕМ КУРСУ Статично невизначні системи і їх ознаки Література: /1/ с.309-316; /2/ 193-198; /3/ с.233-238; /4/ с.101-102; /5/ с.129-132. Основні поняття та ключові слова розділу: статично невизначні системи, зайві в’язі, властивості статично невизначних систем. Поняття про статично невизначні системи (надалі – СНС). Визначення кількості зайвих в’язей. Властивості статично невизначних систем: наявність зайвих в’язей, що підвищує несучу здатність; більша, ніж у статично визначних системах, жорсткість; залежність внутрішніх зусиль від співвідношення жорсткостей елементів конструкцій; температурні впливи та переміщення опор призводять до виникнення внутрішніх зусиль. Методи розрахунку статично невизначних систем. Питання та завдання для самоконтролю 1 Що таке статично невизначна система? 2 Основна ознака статично невизначної системи. 3 Властивості статично невизначних систем та їх обґрунтування. 4 Основні методи розрахунку СНС. Метод сил Література: /1/ с.316-349, 361-368; /2/ 198-231, 238-249; /3/ с.238-258; /4/ с.102-131; /5/ с.132-135, 154-191. Основні поняття та ключові слова розділу: ступінь статичної невизначності системи, основна система та основні невідомі, канонічні рівняння, матриця податливості, вектор вільних членів, ортогональні епюри. Ступінь статичної невизначності плоских систем. Сутність методу сил. Основна система методу сил. Канонічні рівняння. Обчислення і перевірка коефіцієнтів та вільних членів канонічних рівнянь. Матриця податливості системи й вектор вільних членів канонічних рівнянь. Ортогоналізація епюр. Побудова епюр внутрішніх зусиль (М, Q, N) та їх перевірка. Загальний алгоритм розрахунку статично невизначних систем методом сил. Визначення переміщень у статично невизначних системах. Урахування симетрії. Матрична форма методу сил. Розрахунок СНС на зміну температури та переміщення опор. Методичні вказівки Метод сил є одним із основних для розрахунку СНС. Його засвоєння необхідне при подальшому проектуванні конструкцій, будівель і споруд та успішного вивчення інших тем курсу. Важливо навчитися визначати кількість невідомих методу сил (ступінь статичної невизначності системи). У методі сил використовується система, яка називається основною системою. Вона отримується із заданої системи шляхом відкидання умовно зайвих в’язей і навантаження її зовнішніми силами та зусиллями відкинутих зайвих в’язей. Ці зусилля називають основними невідомими методу сил, які зазвичай позначають Важливо засвоїти сутність коефіцієнтів і вільних членів канонічних рівнянь методу сил і звернути увагу на їх знаки та виконання умови Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою методу Мора. При цьому інтеграли Мора можна вираховувати відповідно до правила Верещагіна або за формулою Сімпсона-Корноухова. При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням сумарної епюри внутрішніх зусиль від одиничних навантажень. Для симетричних систем значних спрощень можна досягти, враховуючи їх симетрію. При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження вільних членів канонічних рівнянь. Епюри внутрішніх зусиль для заданої статично невизначної системи будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою
де
Л – ступінь статичної невизначності системи. Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом: 1. За допомогою формули (1) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи. 2. Кожен стрижень системи розглядаємо як балку з шарнірними опорами в кінцевих перерізах, для якої будуються епюри M і Q від зовнішнього навантаження стрижня та моментів, що обчислені в пункті 1. Об’єднавши відповідні епюри M і Q стрижнів системи, отримуємо епюри M і Q для заданої системи. 3. Епюру поздовжніх зусиль (N) будуємо шляхом використання умов рівноваги окремих вузлів системи. Після побудови епюр внутрішніх зусиль необхідно виконати їх статичну й кінематичну перевірки. Знаходження переміщень у статично невизначних системах виконується так, як і в статично визначних, із використанням методу Мора. Наприклад, у балках та рамах переміщення, пов’язане зі згином, обчислюється за формулою
де
Використання обчислювальної техніки зменшує трудомісткість розрахунку статично невизначних систем методом сил. При цьому найбільш раціональною є матрична форма розв’язання задачі.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.24 (0.01 с.) |

 . Для основної системи методу сил можна записати умови її еквівалентності заданій системі у формі рівнянь нерозривності переміщень у перерізах, де відкинуті зайві в’язі. Деяка і -та умова еквівалентності відображає те, що переміщення перерізу (перерізів), де прикладена і -та основна невідома в напрямку її дії від основних невідомих, зовнішнього навантаження й інших впливів, дорівнює нулю. Як правило, умови еквівалентності записують у канонічній формі і називаються канонічними рівняннями методу сил. Кількість канонічних рівнянь, як правило, дорівнює ступеню статичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі.
. Для основної системи методу сил можна записати умови її еквівалентності заданій системі у формі рівнянь нерозривності переміщень у перерізах, де відкинуті зайві в’язі. Деяка і -та умова еквівалентності відображає те, що переміщення перерізу (перерізів), де прикладена і -та основна невідома в напрямку її дії від основних невідомих, зовнішнього навантаження й інших впливів, дорівнює нулю. Як правило, умови еквівалентності записують у канонічній формі і називаються канонічними рівняннями методу сил. Кількість канонічних рівнянь, як правило, дорівнює ступеню статичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі.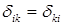 , згідно з теоремою про взаємність переміщень. Основна система повинна бути вибрана таким чином, щоб епюри внутрішніх зусиль від одиничних і зовнішніх навантажень були якомога простими й взаємно ортогональними. При цьому рекомендується розглянути декілька варіантів основних систем і, порівнюючи їх, вибрати раціональну.
, згідно з теоремою про взаємність переміщень. Основна система повинна бути вибрана таким чином, щоб епюри внутрішніх зусиль від одиничних і зовнішніх навантажень були якомога простими й взаємно ортогональними. При цьому рекомендується розглянути декілька варіантів основних систем і, порівнюючи їх, вибрати раціональну.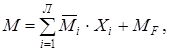 (1)
(1) – епюра згинальних моментів в основній системі від
– епюра згинальних моментів в основній системі від 
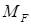 – епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;
– епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;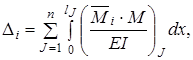
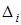 – будь-яке лінійне або кутове переміщення;
– будь-яке лінійне або кутове переміщення;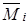 – функція згинального моменту, яка складена для j -ї ділянки інтегрування у допоміжному (одиничному) стані будь-якоїосновної системи методу сил;
– функція згинального моменту, яка складена для j -ї ділянки інтегрування у допоміжному (одиничному) стані будь-якоїосновної системи методу сил;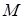 – функція згинального моменту, яка складена для j -ї ділянки інтегрування у заданій статично невизначній системі.
– функція згинального моменту, яка складена для j -ї ділянки інтегрування у заданій статично невизначній системі.


