
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пороговая кинетическая энергия налетающей частицы, вызывающей ядерную реакциюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Т п = Энергия Ферми в металле при Т = 0 К где n - концентрация электронов в металле, m e- масса электрона. Е F =
Концентрация электронов, энергия которых заключена в пределах от e до e+de (при e < ЕF) d n (e) =
Удельная проводимость примесных Полупроводников где e - элементарный заряд, n p и n n - концентрация дырок и электронов, b p и b n - подвижность дырок и электронов. g = e (n p b p + n n b n),
Температурная зависимость проводимости в Полупроводниках где D Е - ширина запрещенной зоны, gо - константа, k - постоянная Больцмана. g = gоexp ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Найти дебройлевскую длину волны электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра
Тэл
  (1) (1)
Имея в виду, что энергия покоя электрона Е 0 =
Выражение для длины волны де Бройля, с учетом (1) и (2), принимает вид:
Произведем вычисления по формуле (3):
Проверим размерность lВ: [lВ ] =
Ответ: Длина волны де Бройля для рассматриваемых электронов равна 3,3×10-12 м или 3,3 пм.
Пример 2. Среднее время жизни атома в возбужденном состоянии составляет t» 1×10-8 сек. При переходе атома в нормальное состояние испускается фотон, средняя длина волны которого равна 500 нм. Определить относительную (
Продифференцировав (2) по l, получим:
Учитывая, что дифференциал d E и приращение D E отличаются на бесконечно малую величину, можно из соотношений (2) и (3) выражение для относительной ширины спектральной линии:
И, наконец, используя (1), приведем (4) к окончательному виду:
Проверим размерность полученного выражения:
И, наконец, вычислим значение (
2) Естественная ширина резонансной линии при этом равна: Dlmin ³ 2,65×10-8×l = 2,65×10-8×5×10-7 = 13,25×10-15 м» 0,0013 пм.
Ответ: Относительная ширина излучаемой спектральной линии равна 2,65
Пример 3. Нормированная собственная волновая функции, описывающая движение электрона в основном состоянии атома водорода имеет вид
тицы можно вычислить следующим образом:
где Кулоновская сила притяжения электрона к ядру в атоме водорода равна
Произведем вычисления по формуле (2):
Ответ: Среднее значение кулоновской силы, действующей на 1s–электрон в атоме водорода равно 0,165 мкН.
Пример 4. За время
Прологарифмировав это соотношение, найдем постоянную распада l:
Воспользовавшись известным соотношением между l и Т, найдем период полураспада:
Найдем массу изотопа 193Hg, имевшего активность А 1 = 1,18 1014 Бк, воспользовавшись следующими соотношениями: ; А 1 = l N 1. Следовательно: (2) Определим численное значения т 1 по формуле (2):
Ответ: Радиоактивный нуклид в данном случае – это изотоп ртути-193; масса изотопа 193Hg равна 1,18 мг.
Пример 5. Определить мощность поглощенной дозы в воздухе и мощность эквивалентной дозы в биологической ткани на расстоянии 1 м от точечного источника
Разделив это выражение на площадь сферы радиуса R, мы получим плотность потока частиц: Число частиц, поглощенных объемом d V (длиной l и площадью d S) за время d t, в соответствии с законом Бугера I = I 0e-k x для поглощения электромагнитного излучения веществом, равно:
Считая, что l << k-1, и разложив в ряд exp (-k l)» 1 – k l, получим:
Умножив (5) на энергию
Далее, разделив d E на массу объема d V (m = r×d V) и подставив в полученное выражение соотношение (3), мы получим в соответствии с (2) поглощенную дозу:
Соответственно, мощность дозы P o равна: P o = Проверим размерности:
Теперь найдем численное значение мощности поглощенной дозы по формуле (8): P o = 2) Мощность эквивалентной дозы будем рассчитывать по формуле: P Н = d H /d t, (9) где Н = Кg × D – поглощенная доза в биологической ткани, Кg = 1 – коэффициент качества для g-излучения. Поглощенную дозу в биологической ткани найдем, заменив в (4) Тогда мощность эквивалентной дозы будет равна:
P Н =
Произведем вычисления по формуле (10): P Н =
Ответ: Мощность поглощенной дозы P D = 8,15×10-7 Гр/сек; мощность эквивалентной дозы в биологической ткани P H = 8,98×10-10
Пример 6. Вычислить дефект массы, энергии связи и удельную энергию связи ядра где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов, составляющих ядро); т р ;т n ;т я– массы протона, нейтрона и ядра, соответственно. В справочных таблицах всегда даются массы нейтральных атомов, но не ядер. Поэтому (1) необходимо преобразовать таким образом, чтобы в него входила масса нейтральных атомов. Массу ядра можно выразить через массу атома и массу электронов атома: т я = т а -Zте. (2) Подставив (2) в (1), получим:
Здесь (тр+тe)=
Для ядра Используемые здесь значения масс атомов и элементарных частиц приведены в табл.16 и табл.17. Энергия связи – разность энергий покоя свободных нуклонов, составляющих ядро, и энергии покоя целого ядра. В соответствии с формулой Эйнштейна, связывающей энергию и массу:
В системе СИ используют размерности: [ В ядерной физике используют для удобства внесистемные единицы энергии: 1 МэВ = 1,6×10-13 Дж и массы: 1 а.е.м. = 1,67×10-27 кг. Соответственно меняется и значение «с2» в (5) при переходе к таким единицам: Таким образом, при использовании внесистемных единиц формула (5) примет вид:
Для Ответ: Для ядра
Пример 7. p 0 - мезон образовался при бомбардировке протонов мишени пучком протонов: р + р
Для релятивистских частиц связь между энергией и импульсом имеет вид: Закон сохранения энергии в рассматриваемом случае можно представить так:
или, с учетом (1), Возведем в квадрат обе части равенства (2) и упростим полученное выражение с учетом того, что
Þ Окончательно выражение для пороговой энергии p 0 имеет вид:
Используя данные для масс элементарных частиц (табл.17), найдем значение Тр:
Ответ: Пороговая энергия образования p 0-мезона равна 279,7 МэВ.
Пример 8. Определить относительную долю свободных электронов в металле при температуре Т = 0 К, энергия которых заключена в
ы ыинтервале от 0 до ½ Е F.
Из этого выражения можно найти концентрацию электронов в металле:
Концентрация электронов, энергия которых заключена в пределах от e до e+de (при e < ЕF), равна: d n (e) = Проинтегрировав это выражение в интервале от 0 до ½ Е F, мы получим концентрацию D n электронов при температуре Т = 0 К, эне
И, окончательно, разделив (4) на (2), получим относительную долю свободных электронов в металле при температуре Т = 0 К, энергия которых заключена в интервале от 0 до ½ Е F:
Ответ: при T = 0 К доля свободных электронов, энергия которых заключена в интервале от 0 до 1/2ЕF, равна 0,354.
ВАРИАНТЫ ЗАДАЧ
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1040; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ×½ Q ½.
×½ Q ½. ×(3p2 n)2/3,
×(3p2 n)2/3,

 ,
, = 10 пм.
= 10 пм. (то есть Тэл одного порядка величины с Е 0), можно сделать вывод, что рассматриваемые электроны являются релятивистскими. В этом случае их импульс определяется соотношением:
(то есть Тэл одного порядка величины с Е 0), можно сделать вывод, что рассматриваемые электроны являются релятивистскими. В этом случае их импульс определяется соотношением: (2)
(2)
 . (3)
. (3)
 .
. .
. ) и естественную ширину Dl получаемой спектральной линии, если не происходит ее уширения за счет других процессов.
) и естественную ширину Dl получаемой спектральной линии, если не происходит ее уширения за счет других процессов. . (3)
. (3) или
или 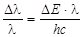 . (4)
. (4) . (5)
. (5) .
. ):
):
 10-8, а естественная ширина Dlmin» 0,0013 пм.
10-8, а естественная ширина Dlmin» 0,0013 пм. , (а 0 – первый боровский радиус). Найти для основного состояния атома водорода среднее значение
, (а 0 – первый боровский радиус). Найти для основного состояния атома водорода среднее значение  - кулоновской силы притяжения электрона к ядру.
- кулоновской силы притяжения электрона к ядру. определяет вероятность нахождения квантовой частицы в единичном объеме в окрестностях точки с координатами х,y,z. Учитывая статистический смысл квадрата модуля волновой функции, среднее значение любого параметра квантовой час-
определяет вероятность нахождения квантовой частицы в единичном объеме в окрестностях точки с координатами х,y,z. Учитывая статистический смысл квадрата модуля волновой функции, среднее значение любого параметра квантовой час-
 , (1)
, (1) - функция, определяющая зависимость данного параметра микрообъекта от положения микрочастицы в пространстве.
- функция, определяющая зависимость данного параметра микрообъекта от положения микрочастицы в пространстве.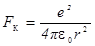 . Учитывая, что волновая функция, описывающая поведение 1s-электрона в атоме водорода, обладает сферической симметрией (см. условие), в данном случае в качестве элементарного объема в (1) имеет смысл использовать объем шарового слоя радиусом r и толщиной d r. В итоге выражение (1) для усредненной кулоновской силы принимает вид:
. Учитывая, что волновая функция, описывающая поведение 1s-электрона в атоме водорода, обладает сферической симметрией (см. условие), в данном случае в качестве элементарного объема в (1) имеет смысл использовать объем шарового слоя радиусом r и толщиной d r. В итоге выражение (1) для усредненной кулоновской силы принимает вид: . (2)
. (2)

 сутки активность изотопа уменьшилась от А 1 = 118 ТБк до А 2 = 7,4 ТБк. Пользуясь таблицей периодов полураспада, определить природу изотопа. Найти также массу изотопа, имеющего активность А 1.
сутки активность изотопа уменьшилась от А 1 = 118 ТБк до А 2 = 7,4 ТБк. Пользуясь таблицей периодов полураспада, определить природу изотопа. Найти также массу изотопа, имеющего активность А 1. = t 2 -t 1= 1сут.
= t 2 -t 1= 1сут. ; т 1.
; т 1.
 (1)
(1) .
.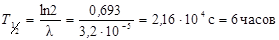
 По таблице периодов полураспада радиоактивных изотопов (см. Табл.18) находим, что рассматриваемый период Т = 6 час. соответствует изотопу ртути 193Hg.
По таблице периодов полураспада радиоактивных изотопов (см. Табл.18) находим, что рассматриваемый период Т = 6 час. соответствует изотопу ртути 193Hg.
 .
. - квантов с активностью 10 мКи. Выход
- квантов с активностью 10 мКи. Выход 
 .
. (3)
(3)
 . (5)
. (5) . (6)
. (6) . (7)
. (7) . (8)
. (8) .
. В выражения (7) и (8) входит массовый коэффициент поглощения в воздухе
В выражения (7) и (8) входит массовый коэффициент поглощения в воздухе  для энергии eg = 1,3 МэВ. Значение этого коэффициентаможно получить из Табл.19 линейной интерполяцией
для энергии eg = 1,3 МэВ. Значение этого коэффициентаможно получить из Табл.19 линейной интерполяцией  м2/кг.
м2/кг. Гр/сек.
Гр/сек. в воздухе на массовый коэффициент поглощения в мягкой ткани
в воздухе на массовый коэффициент поглощения в мягкой ткани  , который также найдем из Табл.19 путем линейной интерполяции
, который также найдем из Табл.19 путем линейной интерполяции  м2/кг.
м2/кг. (10)
(10)
 .
. . (3)
. (3) – масса атома водорода и поэтому окончательно имеем:
– масса атома водорода и поэтому окончательно имеем: . (4)
. (4) а.е.м.
а.е.м. . (5)
. (5) ] = кг; [с2] = м2/с2.
] = кг; [с2] = м2/с2.
 . (6)
. (6) и, соответственно, удельная энергия связи
и, соответственно, удельная энергия связи  .
. р + р + p 0. Определить пороговую энергию образования p 0 - мезона.
р + р + p 0. Определить пороговую энергию образования p 0 - мезона. Закон сохранения импульса, при условии, что протон мишени считается покоящимся, запишем в виде:
Закон сохранения импульса, при условии, что протон мишени считается покоящимся, запишем в виде: (1)
(1) , где
, где  - энергия покоя частицы.
- энергия покоя частицы. ,
, (2)
(2)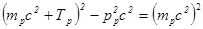 .
. Þ
Þ
 (3)
(3) МэВ.
МэВ.
 . (2)
. (2) . (3)
. (3)
 =
=  (4)
(4)
 ´
´  =
=  = 0,354
= 0,354


