
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Эйнштейна для внешнего фотоэффектаСодержание книги Поиск на нашем сайте hn = A + Tmax, Tmax = mov2max/2 при hn << moс2,
Tmax = (m - mo)c2 при hn ~ moс2,
где h n – энергия фотона; А – работа выхода электронов; T max – максимальная кинетическая энергия фотоэлектронов.
Красная граница внешнего фотоэффекта
lо = hc/A или nо = A/h.
Изменение длины волны рентгеновского (или гамма) излучения при рассеянии на свободном электроне (эффект Комптона) Dl = l/ - l = 2h/moc×sin2q/2 = h/moc×(1- cosq)= lC×(1- cosq),
где l/ - l – длины волн падающего и рассеянного излучения, соответственно; lC = h/moc – комптоновская длина волны; m o – масса покоя электрона; с – скорость света в вакууме; q – угол рассеяния кванта излучения. Давление света при нормальном падении на поверхность
где Ee – энергетическая освещенность (энергия фотонов, падающих в единицу времени на единицу поверхности); w – объемная плотность энергии излучения; r – коэффициент отражения. Плотность энергии излучения
где Е – напряженность электрического поля электромагнитной волны.
Примеры решения задач
Пример 1. Между двумя плоскопараллельными пластинами на расстоянии L = 10 см от границы их соприкосновения находится проволока диаметром D = 0,01 мм, образуя воздушный клин (рис. 5.1). Пластины освещаются нормально падающим монохроматическим светом (λ = 0,6 мкм). Определить расстояние между соседними интерференционными полосами, наблюдаемыми в отраженном свете.
Решение. Стеклянные пластинки образуют в данном случае воздушный клин с малым углом α (рис. 5.1). Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани клина. Эти отраженные лучи когерентны и на поверхности клина будут наблюдаться интерференционные полосы. Так как угол клина мал, то отраженные лучи «1» и «2» будут практически параллельны (рис. 5.1). Найдем расстояние b между двумя соседними темными интерференционными полосами. Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки, равна
где добавочная половина длины волны По условию задачи угол падения равен i = 0o; показатель преломления материала воздушного клина п = 1 (воздух). При этих условиях (105) принимает вид:
где dk – толщина воздушного клина в рассматриваемом месте.
Темные полосы мы видим на тех участках клина, где разность хода лучей кратна нечетному числу половин длины волны:
Объединив соотношения (106) и (107), можно записать условия наблюдения темных полос с номерами «k» и «k+1», соответственно,
и
Вычитая из выражения (109) выражение (108), получим
и окончательно
Исходя из геометрии хода лучей (рис. 5.1), угол клина можно определить двояко:
Произведем расчет величины расстояния между соседними полосами:
Ответ. Расстояние между соседними интерференционными полосами равно 3 мм. Пример 2*. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (l = 650 нм). Диаметр четвертого темного кольца в проходящем свете D 4 = 5,7 мм. Определить радиус кривизны линзы.
Решение. Радиус кривизны линзы R можно найти из условия наблюдения темных колец Ньютона в проходящем свете:
r k =
Для диаметра четвертого темного кольца получим:
D 4 = 2
Из уравнения (112) находим радиус кривизны R линзы:
Произведем расчет по формуле (113):
Ответ. Радиус кривизны линзы составляет 25 м.
Пример 3*. На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет от гелий-неонового лазера (рис. 5.3). Постоянная решетки равна d = 0,01 мм. На экране, удаленном от решетки на расстояние l = 40 см, наблюдаются интерференционные максимумы, при этом расстояние между симметричными максимумами второго порядка составляет x 2 = 100 мм. Найти длину волны гелий-неонового лазера.
Решение. Длину волны гелий-неонового лазера можно найти из условия образования главных максимумов интенсивности света при дифракции на дифракционной решетке: d×sinj = ±k×l, k = 0, 1, 2, 3,.... Отсюда находим:
где d - постоянная дифракционной решетки, k - порядок максимума света, l - длина световой волны.
Выразим sinj через расстояние l между дифракционной решеткой и экраном и расстоянием x между серединами симметричных максимумов k-го порядка (рис. 5.3). Для небольших углов дифракции можно приближенно записать:
sinj @ tgj =
Подставляя полученное значение для sinj в формулу (114), получим формулу для определения длины волны лазера:
Произведем вычисления по формуле (116):
Ответ. Длина волны гелий-неонового лазера l @ 0,63 мкм = 630 нм.
Пример 4*. На поверхность дифракционной решетки нормально к ее поверхности падает параллельный пучок естественного света. Постоянная решетки равна d = 0,01 мм. На экране, удаленном от решетки на расстояние l = 30 см, наблюдаются интерференционные максимумы в виде спектров, при этом расстояние между симметричными максимумами второго порядка красного цвета составляет x 2,кр = 78 мм, а расстояние между симметричными максимумами второго порядка фиолетового цвета составляет x 2,ф = 52 мм. Найти длины волн для красной и фиолетовой линий.
Решение. Длину волны линии спектра можно найти из условия образования главных максимумов интенсивности света при дифракции на дифракционной решетке: d× sinj = ±k×l, k = 0,1,2,3,..., где d - постоянная дифракционной решетки, k - порядок максимума света, l - длина световой волны. Из этого соотношения находим:
Выразим sinj через расстояние l между дифракционной решеткой и экраном и расстоянием x между серединами симметричных максимумов k-го порядка (рис. 5.4). Для небольших углов дифракции можно приближенно записать:
sinj @ tgj =
Окончательно, подставив полученное значение для sinj в формулу (117), получим формулу для определения длины волны полосы в спектре:
Произведем вычисления по формуле (119):
Ответ. Длина волны красной линии спектра lкр @ 0,65 мкм = 650 нм, а длина волны фиолетовой линии спектра lф @ 0,43 мкм = 430 нм
Пример 5. Луч света проходит через жидкость, налитую в стеклянный сосуд (п ст= 1,50), и отражается от дна. Отраженный луч оказывается полностью поляризованным при угле падения на дно сосуда i = 49o. Определить, под каким углом должен падать на дно сосуда луч света, проходящий в этой жидкости, чтобы наблюдалось полное внутреннее отражение от поверхности жидкости (рис. 5.5).
Решение. По закону Брюстера свет, отраженный от поверхности диэлектрика, полностью поляризован при условии, что
tg iB = n21 = n2/n1. (120)
Отсюда
n1 = n2 / tg iB. (121)
При полном внутреннем отражении от поверхности жидкости (r2 = 90о)закон преломления на поверхности жидкости примет вид:
Таким образом, угол падения луча света i 2 на дно сосуда при полном внутреннем отражении от поверхности жидкости равен:
Подставив в (122) выражение (121) для n 1, окончательно получим:
Ответ. Чтобы наступило полное внутреннее отражение от поверхности жидкости, луч света должен падать на дно сосуда под углом 50˚.
Пример 6. Монохроматический пучок световых лучей проходит через стопу из пяти одинаковых плоскопараллельных стеклянных пластинок толщиной 5 мм каждая. Отношение интенсивности света, прошедшего через эту стопу пластинок, к интенсивности падающего света равно t = 0,55. Пренебрегая вторичным отражением света, определить коэффициент поглощения k для данного стекла, если коэффициент отражения на каждой поверхности пластинок r = 0,05.
По закону Бугера интенсивность света, прошедшего слой вещества толщиной x, равна:
I = I0×e-kx, (123)
где I 0 – интенсивность падающего пучка, а k – коэффициент поглощения света в стекле.
Согласно (1) с учетом отражения света от верхней поверхности пластинки, до 2-й грани первой пластинки доходит свет с интенсивностью I0×(1-r)e-kl. На второй грани часть световой энергии также отражается, то есть на выходе из 1-й пластинки имеем свет с интенсивностью:
I1 = I0×(1-r)2e-kl. (124)
По аналогии можно показать, что на выходе из 2-й пластинки интенсивность светового пучка будет равна:
I2 = I1×(1-r)2e-kl = I0×(1-r)4e-2kl. (125)
Анализируя выражения (124) и (125), можно сделать вывод, что на выходе из стопы в N пластинок интенсивность света будет равна:
IN = I0×(1-r)2Ne-Nkl. (126)
Преобразуем выражение (126) следующим образом:
IN / I0 = (1-r)2Ne-Nkl Þ t = (1-r)2Ne-Nkl Þ
Отсюда находим:
Найдем численное значение k:
Ответ. Коэффициент поглощения данного сорта стекла равен 0,034 см-1.
Пример 7. При исследовании излучения серого тела (с поглощательной способностью А Т = 0,25 и потоком излучения Фе = 1 кВт) системой из узкополосных светофильтров было установлено, что максимальная мощность излучения (прошедшего через один из светофильтров) равна W = 6,25 мВт. Принять во внимание, что: до приемника излучения (с учетом геометрии его расположения и потерь в оптической системе) доходит 10 % мощности, излучаемой телом; площадь светофильтра равна Sсф = 1 см2; энергия излучения распределена в полосе пропускания светофильтра (
Из выражения для максимального значения спектральной плотности излучательности и закона смещения Вина найдем температуру тела и длину волны, на которую рассчитан светофильтр:
Произведем вычисления по формулам (1) и (2):
2) Исходя из закона Стефана-Больцмана R e = s× T 4, найдем площадь излучающей поверхности серого тела:
Произведем вычисления:
Ответ: Светофильтр рассчитан на длину волны
Пример 8. Фотон с энергией eф = 20 эВ падает на металлическую пластину и вызывает фотоэффект. Пластина получает при этом импульс pпл = 2,19
а импульс фотоэлектрона p e может быть найден из уравнения Эйнштейна для внешнего фотоэффекта
где А – работа выхода электрона из металла – индивидуальная (см. Табл.14) характеристика каждого металла, m e – масса электрона, v e – скорость электрона. Так как p e = m e× v e, получаем:
Очевидно, что, определив А, можно по справочным таблицам найти, о каком металле идет речь. Подставив выражения (3) и (5) в (2), получим:
Из этого соотношения (6) находим А:
По табл.14 для работ выхода электронов находим, что такой работой выхода обладает Al (алюминий). Ответ: Фотоэффект происходит на алюминиевой пластине.
Пример 9. При эффекте Комптона фотон с длиной волны λ = 1,2 пм был рассеян на свободном электроне. Импульс электрона отдачи составил при этом pe = 6×10-22 кг×м/сек. Определить длину волны рассеянного излучения и угол рассеяния.
Кинетическая энергия электрона, соответственно, равна: Т = Е – Е 0 = 19,8×10-14 – 8,16
Длину волны рассеянного излучения найдем из закона сохранения энергии
На основании найденного значения энергии
2) Угол рассеяния фотона при эффекте Комптона qопределим в соответствии с формулой Комптона:
Следовательно,
Ответ: Угол рассеяния фотона при эффекте Комптона составляет 98,40; при этом длина волны рассеянного излучения равна 3,98 пм.
Пример 10. На расстоянии r = 5 мот точечного изотропного монохроматического источника (
2) Сила давления F давл, действующая на зачерненную площадку, равна:
где
Произведем вычисления по формуле (1):
Ответ: Число фотонов, ежесекундно падающих на площадку, составляет 6,35×1016 с-1; сила давления света на поверхность S равна 8,5
Варианты задач
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1055; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (1+r) = w (1+r),
(1+r) = w (1+r),

 1 2
1 2
Ddk
dk+1
dk
a D
L k b k+1
Рис. 5.1
1 2
1 2
Ddk
dk+1
dk
a D
L k b k+1
Рис. 5.1
 (105)
(105) обусловлена отражением волны от оптически более плотной среды (происходит в данном случае при отражении луча «2» от нижней грани воздушного клина).
обусловлена отражением волны от оптически более плотной среды (происходит в данном случае при отражении луча «2» от нижней грани воздушного клина). (106)
(106)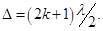 (107)
(107)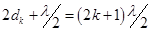 (108)
(108) (109)
(109)
 (110)
(110) и
и  Из этих соотношений, после подстановки в них (110), находим:
Из этих соотношений, после подстановки в них (110), находим: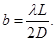
 м
м 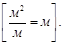
 R
r
d
Рис. 5.2
R
r
d
Рис. 5.2
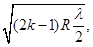 k = 1,2,.... (111)
k = 1,2,.... (111) (112)
(112) (113)
(113) = 25 м
= 25 м
 k k = 2
x
j
k k = -2
l
Рис. 5.3
k k = 2
x
j
k k = -2
l
Рис. 5.3
 (114)
(114) (115)
(115) (116)
(116) 0,63×10-6 м = 0,63 мкм = 630 нм
0,63×10-6 м = 0,63 мкм = 630 нм


 кр
кр
 k = 2
ф
x
j
ф
k = -2
кр
l
Рис.5.4
k = 2
ф
x
j
ф
k = -2
кр
l
Рис.5.4
 (117)
(117) = 0,65×10-6 м = 0,65 мкм = 650 нм,
= 0,65×10-6 м = 0,65 мкм = 650 нм, @ 0,43×10-6 м = 0,43 мкм = 430 нм.
@ 0,43×10-6 м = 0,43 мкм = 430 нм. n 0 r2
S * i 2
n 1 i 2 i 2
n 2
Рис. 5.5
n 0 r2
S * i 2
n 1 i 2 i 2
n 2
Рис. 5.5


 (122)
(122)

 где I 0 - интенсивность пучка на входе в первую пластинку.
где I 0 - интенсивность пучка на входе в первую пластинку.


 м-1 = 0,034 см-1.
м-1 = 0,034 см-1. нм) равномерно. Определить, на какую длину волны рассчитан светофильтр, пропустивший максимальную мощность. Найти также температуру тела и площадь его излучающей поверхности.
нм) равномерно. Определить, на какую длину волны рассчитан светофильтр, пропустивший максимальную мощность. Найти также температуру тела и площадь его излучающей поверхности.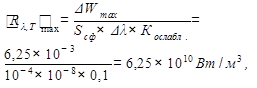 где Кослабл – коэффициент ослабления излучения в оптической системе.
где Кослабл – коэффициент ослабления излучения в оптической системе.
 Вт/ м3.
Вт/ м3. Þ
Þ  (1)
(1) (2)
(2)

 мкм.
мкм.


 = (1,620
= (1,620  0,005 ) мкм; температура исследуемого тела равна 1780 К, а площадь его излучающей поверхности равна 70 см2.
0,005 ) мкм; температура исследуемого тела равна 1780 К, а площадь его излучающей поверхности равна 70 см2. Импульс фотона можно записать в виде:
Импульс фотона можно записать в виде: , (3)
, (3) (4)
(4) (5)
(5) = p пл -
= p пл -  . (6)
. (6) (7)
(7) Определим, согласно (7), работу выхода электрона из металла.
Определим, согласно (7), работу выхода электрона из металла.
 Е =
Е =  Дж.
Дж.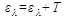 , где el - энергия падающего фотона,
, где el - энергия падающего фотона,  - энергия рассеянного фотона. Отсюда, с учетом того, что
- энергия рассеянного фотона. Отсюда, с учетом того, что  , находим:
, находим: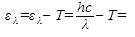
 .
.

 .
. ;
; 
 мкм) расположена зачерненная площадка (S = 8 см2), ориентированная перпендикулярно падающим лучам. Определить число фотонов, ежесекундно падающих на площадку, и силу давления света, действующую на нее. Поток излучения источника равен 10 кВт.
мкм) расположена зачерненная площадка (S = 8 см2), ориентированная перпендикулярно падающим лучам. Определить число фотонов, ежесекундно падающих на площадку, и силу давления света, действующую на нее. Поток излучения источника равен 10 кВт.

 с-1
с-1  .
.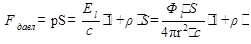
 - коэффициент отражения зачерненной площадки.
- коэффициент отражения зачерненной площадки. Н
Н  .
.


