Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разработка концептуальной модели объектаСодержание книги
Поиск на нашем сайте
Содержание Введение 3 1. Разработка концептуальной модели объекта 4 2. Математическая модель объекта 7 2.1 Модель динамики объекта 8 2.2 Модель статики 9 3. Оптимизация объекта 10 4. Представления объекта, как объекта управления 17 4.1. Построение статических характеристик объекта по различным каналам 18 4.2. Построение динамических характеристик по каналам регулирования и каналам возмущения 20 5. Анализ исследования статический и динамических характеристик объекта 23 6. Выбор программных средств для моделирования 24 7. Проверка работоспособности модели 25 8. Синтез системы управления двумерным объектом 27 8.1. Расчет регуляторов для системы управления 29 8.2. Расчет передаточных функций компенсаторов 32 9. Показатели качества регулирования 34 9.1. Исследование ковариантности и инвариантности системы управления 35 9.2. Оценка ковариантности САУ 37 9.3. Оценка инвариантности САУ 39 Заключение 41 Список использованных источников 42
Введение Конечной целью любого производства является получение полезных продуктов путем переработки из исходного сырья наиболее эффективнымспособом. Чтобы технологический процесс функционировал эффективно необходимо осуществить контроль его состояния и формировать управляющее воздействие при отклонении технологических параметров от оптимальных значений. Эту задачу решает автоматизированная система управления технологическим процессом. Первым этапом разработки автоматизированной системы управления технологическим процессом является разработки системы автоматического управления технологическим процессом. Разработка САУ предполагает анализ технологического процесса с целью выявления статических и динамических свойств и характеристик объекта. Эти свойства выражаются в конечном итоге в математической модели объекта, которая может быть разработана аналитически, либо экспериментально, если объект имеется в наличии. Таким образом, для разработки САУ необходима математическая модель технологического процесса. Исходя из выше сказанного, можно сформулировать и задачи курсовой работы. Целью и задачами курсовой работы являются: · Разработка концептуальной и математической моделей технологического процесса;
· Проведение оптимизации процесса функционирования объекта; · Исследование статических и динамических свойств объекта; · Разработка программного обеспечения, для решения выше указанных задач; · Составление системы регулирования в выбранном программном обеспечении; · Исследование системы на инвариантность и ковариантность. Разработка концептуальной модели объекта Объект моделирования – химический реактор емкостного типа, снабжённый механической мешалкой и рубашкой для подогревания жидкости в реакторе. В реактор емкостного типа с механической мешалкой подается исходные реагенты А, B, C, D и поток воды с расходами

Рис. 1 Принципиальная схема процесса Обозначения: υ1, υ2, υ – расходы потоков. t1, t2, t – температуры соответствующих потоков. Caвх, Сbвх, Ccвх, Cdвх – концентрации веществ a, b, c, d на входе в реактор, соответственно. Ca, Сb, Cc, Cd – концентрации веществ a, b, c, d, соответственно. Vp – объем реактора. Vт – объем рубашки. υт – расход теплоносителя. tт – температура теплоносителя. Назначение: проведение в непрерывном режиме химических реакций. Цель функционирования: получение целевых продуктов B, C, D с заданными концентрациями. Классификация переменных
Переменные состояния: O объём реактора - Vp O концентрация компонента А на выходе - Ca O концентрация компонента В на выходе - Cb O концентрация компонента С на выходе - Cc O концентрация компонента D на выходе - Cd O температура в реакторе - t Математическая модель объекта Модель динамики объекта Реакция происходит в четыре стадии:
Запишем скорость реакции по компонентам в систему (2.2.1) в следующем виде:
В соответствии с классификацией переменных и допущениями математическая модель динамики включает в себя:
Уравнения материального баланса по компонентам с условием, что объём постоянен.
Уравнение теплового баланса реакционной смеси.
Уравнение теплового баланса рубашки.
Начальные условия: Vp=Vpo; Ca=Cao; Cb=Cbo; Cc=Cco; Cd=Cdo; t=to: tтн=tтно Модель динамики представляет собой систему нелинейных ОДУ.
Модель статики объекта Уравнения динамики и статики решаем при помощи функции Rkadapt. Данная функция реализует решение системы дифференциальных уравнений методом Рунге-Кутта 4 порядка с адаптивным шагом решения. Уравнения статики при помощи процедуры Given-Find.
3. Оптимизация объекта Определить значение технологических параметров, обеспечивающих минимальный объём аппарата при заданном выходе целевого продукта (ψ=75%), заданной нагрузке, заданных значениях входных переменных, заданных ограничений на температуру t=[70-90оС] Для решения задачи оптимизации используются только уравнения материального баланса по компонентам: Vp * Vp * Vp * Vp * Листинг программы в среде MathCAD:
Зададимся ориентировочными значениями объема и температуры. Пусть V=120 л, t=90˚C. Т.к. целевым компонентом реакции является компонент В, то критерий оптимизации ψb будем рассчитывать по формуле (3.1):
Рассчитывая оптимальные значения температуры и объема, мы задаемся ориентировочной температурой в 70° и изменяем объем в реакторе от 90 до 210, с шагом 10, затем по полученным данным строим график зависимости объема от температуры.
Аналогично проводятся расчеты и для других объемов при температурах 80˚ и 90˚С. В результате получаем следующие значения:
Рис. 3.1. Зависимость объема от температуры при 70, 80 и 90 °С
Из графиков видно, что при φ=75% V=120л и t=90°C, т.е. topt = 90˚C, Vopt = 120л.
Выполним пересчет поверхности теплообмена Ft, учитывая оптимальные значения объема реактора и температуры реакционной смеси в нем, при условии, что D=H.
С помощью блока Given-Find пересчитаем температуру на входе в рубашку, используя уравнения теплового баланса для реактора:
Выполним проверку полученных оптимальных значений. Для этого решим нелинейную модель с начальными условиями, соответствующими найденным значениям выходных переменных в оптимальном режиме (т.е. оптимальные значения Vp, Ca, Cb, Cc, Cd, t) и постоянном объеме. Если не задавать входным переменным приращений, то графики изменения выходных переменных во времени должны представлять собой прямые. Используя уравнения материального баланса по компонентам и теплового баланса жидкости в реакторе, запишем вектор-функцию модели:
Рис. 3.2 Графики зависимости выходных переменных от времени
Т.к. полученные графики – это прямые линии, то можно сделать вывод, что найденные значения параметров являются верными и программное средство написано правильно.
Таблица 2 Построение кривых разгона Динамические свойства объекта исследовались путем расчета реакции объекта на ступенчатое изменение входных переменных. Ступенчатое изменение входной переменной задавалось путем соответствующего изменения значения в уравнении (увеличение или уменьшение на 20 %). Начальные условия интегрирования принимались равными значениям в статике.
Динамическая характеристика по каналу υ2–>Сb
 
рис. 5.1 Динамическая характеристика по каналу (υ2+Δ υ2) –> СВ; Δ υ2=0.05 л/мин
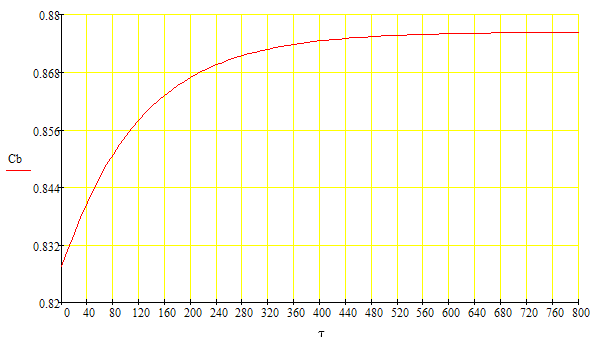 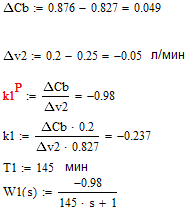
рис. 5.2 Динамическая характеристика по каналу (υ2-Δ υ2) –> СВ; Δ υ2=-0.05 л/мин Динамическая характеристика по каналу υ–>Сb
 
рис. 5.3 Динамическая характеристика по каналу (υ+Δ υ) –> СВ; Δ υ=0.2 л/мин
 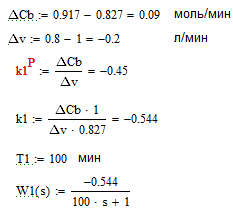
рис. 5.4 Динамическая характеристика по каналу (υ-Δ υ) –> СВ; Δ υ2=-0.2 л/мин
Заключение В ходе проведенной работы был исследован объект - химический реактор и проведен синтез системы управления на его основе. Были исследованы наиболее вероятные каналы управления и возмущения. Смоделирована система автоматического регулирования объектом по данным каналам. В качестве каналов управления рассматривались: влияние потока-разбавителя на концентрацию целевого компонента и влияние расхода на выходе из реактора на объем реакционной смеси. Основными возмущающими воздействиями являются: влияние входной концентрации компонента. А на концентрацию целевого компонента и влияние расхода основного потока на объем реакционной смеси в реакторе. Кроме того, использовали регуляторы по основным каналам управления. Параметры настроек регуляторов для системы управления рассчитаны по биномиальным формам Баттеворта. Химический реактор был исследован на ковариантность к управляющему воздействию и инвариантность к возмущениям. Полученные результаты сведены в итоговую таблицу и сделаны выводы. Программная реализация исследования данного химического реактора осуществлена с помощью программы MATLAB и блока Simulink.
Список использованной литературы 1. Ротач В. Я. Теория автоматического управления теплоэнергетическими процессами. М.: Энергоиздат,1985 2. А.А. Головушкин, Б.А. Головушкин. «Теория автоматического управления». Часть1., «Линейные системы автоматического управления» - Иваново, ИГХТУ. 1993. 3. Кирьянов Д.В. Mathcad 13. СПб.: БХВ,- Петербург, 2006 г. 4. Справка программы MATLAB
Содержание Введение 3 1. Разработка концептуальной модели объекта 4 2. Математическая модель объекта 7 2.1 Модель динамики объекта 8 2.2 Модель статики 9 3. Оптимизация объекта 10 4. Представления объекта, как объекта управления 17 4.1. Построение статических характеристик объекта по различным каналам 18 4.2. Построение динамических характеристик по каналам регулирования и каналам возмущения 20
5. Анализ исследования статический и динамических характеристик объекта 23 6. Выбор программных средств для моделирования 24 7. Проверка работоспособности модели 25 8. Синтез системы управления двумерным объектом 27 8.1. Расчет регуляторов для системы управления 29 8.2. Расчет передаточных функций компенсаторов 32 9. Показатели качества регулирования 34 9.1. Исследование ковариантности и инвариантности системы управления 35 9.2. Оценка ковариантности САУ 37 9.3. Оценка инвариантности САУ 39 Заключение 41 Список использованных источников 42
Введение Конечной целью любого производства является получение полезных продуктов путем переработки из исходного сырья наиболее эффективнымспособом. Чтобы технологический процесс функционировал эффективно необходимо осуществить контроль его состояния и формировать управляющее воздействие при отклонении технологических параметров от оптимальных значений. Эту задачу решает автоматизированная система управления технологическим процессом. Первым этапом разработки автоматизированной системы управления технологическим процессом является разработки системы автоматического управления технологическим процессом. Разработка САУ предполагает анализ технологического процесса с целью выявления статических и динамических свойств и характеристик объекта. Эти свойства выражаются в конечном итоге в математической модели объекта, которая может быть разработана аналитически, либо экспериментально, если объект имеется в наличии. Таким образом, для разработки САУ необходима математическая модель технологического процесса. Исходя из выше сказанного, можно сформулировать и задачи курсовой работы. Целью и задачами курсовой работы являются: · Разработка концептуальной и математической моделей технологического процесса; · Проведение оптимизации процесса функционирования объекта; · Исследование статических и динамических свойств объекта; · Разработка программного обеспечения, для решения выше указанных задач; · Составление системы регулирования в выбранном программном обеспечении; · Исследование системы на инвариантность и ковариантность. Разработка концептуальной модели объекта Объект моделирования – химический реактор емкостного типа, снабжённый механической мешалкой и рубашкой для подогревания жидкости в реакторе. В реактор емкостного типа с механической мешалкой подается исходные реагенты А, B, C, D и поток воды с расходами

Рис. 1 Принципиальная схема процесса
Обозначения: υ1, υ2, υ – расходы потоков. t1, t2, t – температуры соответствующих потоков. Caвх, Сbвх, Ccвх, Cdвх – концентрации веществ a, b, c, d на входе в реактор, соответственно. Ca, Сb, Cc, Cd – концентрации веществ a, b, c, d, соответственно. Vp – объем реактора. Vт – объем рубашки. υт – расход теплоносителя. tт – температура теплоносителя. Назначение: проведение в непрерывном режиме химических реакций. Цель функционирования: получение целевых продуктов B, C, D с заданными концентрациями. Классификация переменных
Переменные состояния: O объём реактора - Vp
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.011 с.) |

 и концентрациями CАвх., CВвх., CСвх., CDвх.. В аппарате происходит эндотермическая реакция с образованием продуктов B, C, D. Смесь из реактора забирается насосом, величина потока может регулироваться клапаном. В рубашку аппарата подаётся теплоноситель. В качестве теплоносителя используется пар. Благодаря интенсивному перемешиванию структура потоков в реакторе может быть описана моделью идеального смешения. Аппарат работает в политропическом режиме.
и концентрациями CАвх., CВвх., CСвх., CDвх.. В аппарате происходит эндотермическая реакция с образованием продуктов B, C, D. Смесь из реактора забирается насосом, величина потока может регулироваться клапаном. В рубашку аппарата подаётся теплоноситель. В качестве теплоносителя используется пар. Благодаря интенсивному перемешиванию структура потоков в реакторе может быть описана моделью идеального смешения. Аппарат работает в политропическом режиме.




 (2.2.1)
(2.2.1)
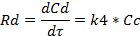







 = Vp*(-k1*CA +k2*CВ)+υ1*CAвх –υ*CA
= Vp*(-k1*CA +k2*CВ)+υ1*CAвх –υ*CA = (k1*CA – k2*CB– k3*CB)* Vp + υ1*СВвх - υ*CB
= (k1*CA – k2*CB– k3*CB)* Vp + υ1*СВвх - υ*CB = (k3*CВ – k4*CC)* Vp + υ1*ССвх - υ*CC
= (k3*CВ – k4*CC)* Vp + υ1*ССвх - υ*CC = k4*CС* Vp + υ1*СDвх - υ*CD
= k4*CС* Vp + υ1*СDвх - υ*CD

 (3.1)
(3.1)