
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 3. «исон. Обсервационный и автономный режимы работы исон на основе биим на вог, па GPS и лага при мореходных испытаниях»Содержание книги
Поиск на нашем сайте
При выполнении лабораторной работы используются результаты натурных испытаний ИБ, в частности: § массивы данных мореходных испытанийИБ на ВОГ с постоянным вращением с периодом 1мин в условиях маневрирования по курсу, сформированные на частоте 100 гц длительностью около 6 ч из результатов проведенных испытаний, которые занесены в память PC; § массивы данных мореходных испытанийстандартной и мультиантенной ПА GPS/ГЛОНАСС,занесенные в память PC; § имитатор данных относительного лагас марковской моделью морских течений; § массивы данных мореходных испытанийкорабельногогирокомпаса имультиантенной ПА GPS/ГЛОНАСС по курсу, занесенные в память PC и используемые (при их совместной обработке для сглаживания шумов ПА GPS – K_gkmr) в качестве эталонной информации). Для реализации обсервационного режима работы БИИМ на ВОГ в условиях эксплуатации используются скоростные (2) и позиционные измерения (3) по GPS. При этом вектор измерения Z примет вид
Перед переходом из обсервационного в автономный режим в течение 1 часа используется не только измерения, сформированные по GPS, но и скоростные измерения по лагу
При реализации автономного режима используются только скоростные измерения по лагу (5)
5.3.1. Дополнение к описанию программного обеспечения
Изменения схемы обработки связано в первую очередь с тем, что в данной работе используются реальные сигналы внешних измерителей (GPS и гирокомпаса), в отличие от режимов, которые исследовались в условиях стенда, т.е. когда эти сигналы формировались с помощью имитатора. Блок 1 (рис. 2) в файле M_IS24re_VG_MrRdr_Lit_f.mdl видоизменился, а именно из массива данных мореходных испытаний (см. рис. 5) используются показания гирокомпаса (K_gk) и МРК (K_mrk). Кроме этого изменения произошли в Блоках 5 и 7 (рис. 6): 1. 2. ключ №3 используется для формирования погрешности приборного курса относительно гирокомпаса (или МРК); 3. ключ №4 используется для формирования в Блоке 7 курсового измерения 4. дополнительно к 7-ми файлам, в которые записываются результаты для последующего построения графиков, в Блоке 5 используются еще два:
§ «файл №8»: Kgkmr_VG_Mr8.mat (результат интегрирования гирокомпаса и МРК); §
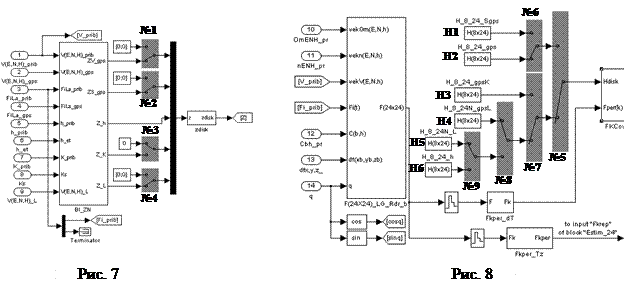
Схема реализации алгоритма ФК (рис. 6, содержание Блока 7) также видоизменилась. При формировании вектора Z скоростные и позиционные измерения по GPS разделены (для настройки используются ключи №1 и 2, см. рис. 7), матрица измерений H выбирается ключами №5…9 (см. рис. 8). Возможные схемы проведения лабораторной работы:
Исходные требования, в зависимости от номера варианта, сведены в таблице 3. Таблица 3.
Действия оператора: III.1. Запустить программу Matlab (ярлык программы III.2. Открыть файл loader_Ncn.m (для этого нажать load 2_Mr4.mat;
n=1440000;
с=100000; % номер стартовой строки массива 2_Mr4.mat Загрузить файл loader_Ncn.m в рабочую область Workspace Matlab, нажав кнопки Debug®Run.
III.3. открыть программу IS24re_VG_MrRdr_dat03_04p1.m § проверить правильность задания или вычисления по значениям первой точки массива данных, загруженных в рабочую область Workspace Matlab, начальных значений (при t=0): · координат места: fio=Fi_s(c,1)*180/pi; % широты lambdao=La_s(c,1)*180/pi; % долготы · скорости: Vo=V_s(c,1); %V_s(c,1) д.б. =0 · параметров ориентации (углы килевой и бортовой качеквычисляются по сигналам акселерометров nsxb(Ax), nsyb(Ay), nszb(Az)): Roo=Gamma(c,1); % угла поворота ИБ БИИМ) Ko=K_mrk(c,1); % курса
nsxb= Ax(c,1); nsyb= Ay(c,1); nszb= Az(c,1); § установить начальные значения погрешностей БИИМ (t=0) (согласно номеру варианта, см. табл. 1) в следующих пределах: Alphao =(см. табл. 1) *pi/180; Betao= (см. табл. 1) *pi/180; Gammao= (см. табл. 1) *pi/180; DVEo= (см. табл. 1); DVNo= (см. табл. 1); DVHo= (см. табл. 1); DFio= (см. табл. 1) *5e-6/30; DLamo= (см. табл. 1) *5e-6/30; Dho= (см. табл. 1); § проверитьввод априорных значений оценок смещения нуля акселерометра по оси zb, смещения нуля и погрешности масштабного коэффициента гироскопа по оси zb, (см. табл. 2, строка “ среднее ”: DAzo =(см. табл. 2); DGzo =(см. табл. 2, с обратным знаком!) *5e-6; DMgzo =(см. табл. 2, с обратным знаком!); § проверитьввод параметров течения (методические погрешности лага), т.е. в модели лага положить: SigmaVTE=0.2; SigmaVTN=0.3; III.4. Загрузить файл IS24re_VG_MrRdr_dat03_04p1.m в рабочую область Workspace Matlab, нажав кнопки Debug ® Run. III.5. Загрузить Simulink (для этого на панели инструментов Matlab нажать III.6. Настроить алгоритм для реализации обсервационного режима БИИМ на ВОГ в условиях эксплуатации: § Подключить измерения ZV_gps, ZS_gps (см. рис. 7 ключи №1 и 2 - “вниз”), а измерения Z_K и Z_L отключить (см. рис. 7, ключи №3 и №4 “ вверх ”). § Подключить матрицу измерений H_8_24_gps (рис. 8, H2, ключ №5 “ вверх ”, а ключ №6 “ вниз ”); III.7. В Блоке 5 (рис. 6) изменить названия всех (9-ти!) file*Mr8.mat (название файла результатов, который формируется в блоке «файл №1», станет Or_VG_ Mr8. mat). III.8. Указать в меню настроек Simulation ® Simulation Parameters (рис. 4) значение параметра stop time равное 13000 с (для 4 ч массива), а также дискретность (dt) и численный алгоритм (Euler) интегрирования. III.9. Запустить процесс обработки массива данных, нажав кнопки Simulation®Start ( или кнопку III.10. ВНИМАНИЕ!!! Через 2.0 ч модельного времени в обсервационном режиме работы ИСОН подключить в обработку данные лага: § Дополнительно подключить измерения Z_L (см. рис. 7 ключ №4 - “вниз”). § Подключить матрицу измерений H_8_24N_gpsL (рис. 8, H4, ключи №5 и 7 “ вниз ”), ключ №8 “ вверх ”). III.11. ВНИМАНИЕ!!! Через 3.0 ч модельного времени переключиться в автономный режим работы ИСОН, для чего: § Подключить измерение Z_L (см. рис. 7, ключ №4 - “ вниз ”), а измерения Z_K, ZV_gps и ZS_gps отключить (см. рис. 7, №1…3 - “вверх ”). § Подключить матрицу измерений H_8_24N_L (рис. 8, H5, ключи №5, №7, №8 “ вниз ”, а ключ №9 -“ вверх ”); III.12.После окончания моделирования построить с использованием программ plot_Kgkmr.m, plot_Or.m, plot_DV.m, plot_DS.m, plot_Dr.m, plot_Dn.m, plot_DMg.m, plot_Krdr.m, plot_DVT.m по значениям, записанным в соответствующие file.mat, графики значений погрешностей ИСОН (по параметрам ориентации, составляющим вектора линейной скорости и координат места) и оценок смещений нулей гироскопов и акселерометров, погрешностей масштабных коэффициентов и коэффициентов румбовых дрейфов. Графики необходимо внести в отчет. Содержание протокола:
1. Время переходного процесса по курсу при запуске системы в обсервационном режиме;
2. Наблюдаемость составляющих моделей погрешностей гироскопов и акселерометров и уровень ошибок их оценок (по анализу работы ковариационного канала ФК); 3. Уровень значений и время переходного процесса для оценок смещений нулей гироскопов и акселерометров, погрешностей масштабных коэффициентов и коэффициентов румбовых дрейфов гироскопов в обсервационном и автономном режимах работы ИСОН (с учетом ввода их априорных значений); 4. Уровень ошибок оценки морских течений; 5. Изменение погрешности ИСОН по курсу в автономном режиме по сравнению с обсервационным режимом; 6. Допустимое время работы ИСОН в автономном режиме (при наличии морских течений) при удержании погрешностей координат места на уровне 100 м.
Содержание итогового отчета В отчете должны быть предусмотрены следующие разделы: 1. Назначение, состав, точностные и надежностные характеристики ИСОН на основе БИИМ на ВОГ. 2. Результаты и их анализ камеральной обработки в пакете Matlab данных стендовых испытаний ИБ БИИМ на ВОГ. 3. Результаты и их анализ камеральной обработки в пакете Matlab мореходных испытаний ИБ БИИМ на ВОГ. Литература
Приложения П1. Программы для обеспечения лабораторных работ kurs№n1.m, loader_Ncn.m, IS24re_VG_StRdr_bqN_dat.m
Программа kurs№n1.m загрузкив рабочую область Workspace Matlab массивов kurs№.mat результатов стендовых испытаний ИБ БИИМ на ВОГ
clear all; load kurs0.mat; n=541000; x=x'; [row, col]=size(x) dlin=1:n; f=50; dt=0.02; time=(dlin)*dt; time=time'; TIME=n*dt; Ax(:,1)=x(dlin,2)-0.0*x(dlin,3)+0.0018*x(dlin,4); Ay(:,1)=x(dlin,3)-0.0*x(dlin,2)+0.0000136*x(dlin,4); Az(:,1)=x(dlin,4)+0.00375*x(dlin,2)+0.0008*x(dlin,3); Gx(:,1)=x(dlin,5)+0.00083*x(dlin,7)-0.0005*x(dlin,6); Gy(:,1)=x(dlin,6)-0.00025*x(dlin,7)-0.0016*x(dlin,5); Gz(:,1)=x(dlin,7)+0.0023*x(dlin,5)+0.0017*x(dlin,6); Gamma(:,1)=x(dlin,8); clear x; Программа loader_Ncn.m загрузкив рабочую область Workspace Matlab массива load 2_Mr.mat результатов мореходных испытаний ИБ БИИМ на ВОГ, стандартной и мультиантенной GPS и компаса clear all; load 2_Mr.mat; dt=0.01; n=2260000;%n=1900000; x=x'; [row, col]=size(x) row=n; c=100000; time(:,1)=x(c:row,1)-x(c,1); Ax(:,1)=x(c:row,2)-0*x(c:row,3)+0.0035*x(c:row,4); Ay(:,1)=x(c:row,3)-0*x(c:row,2)+0.0000136*x(c:row,4); Az(:,1)=x(c:row,4)+0.00375*x(c:row,2)+0.0008*x(c:row,3); Gx(:,1)=x(c:row,5)-0.0005*x(c:row,6)+0.00083*x(c:row,7); Gy(:,1)=x(c:row,6)-0.0016*x(c:row,5)-0.00025*x(c:row,7); Gz(:,1)=x(c:row,7)+0.0023*x(c:row,5)+0.0017*x(c:row,6); Gamma(:,1)=x(c:row,12);
La_s(:,1)=x(c:row,8); Fi_s(:,1)=x(c:row,9); V_s(:,1)=x(c:row,10); K_gku(:,1)=x(c:row,11); Temper(:,1)=x(c:row,13); K_mrk(:,1)=x(c:row,14); clear x;
Программа IS24re_VG_StRdr_bqN_dat.m загрузкив рабочую область Workspace Matlab массива необходимых констант (дискретность поступления данных испытаний ИБ на ВОГ, GPS, компаса и лага, масштабные коэффициенты гироскопов и акселерометров и априорные значения коэффициентов моделей их погрешностей, начальные значения параметров ориентации из режима «грубой» выставки и параметров движения объекта, параметры фигуры и гравитационного поля Земли, значения коэффициентов имитационных моделей погрешностей GPS и лага, значения настройки параметров фильтра Калмана и т.д.) format long; %параметры дискретизации данных dt=0.02; dT=0.02; dT1=0.1; Tz=1; n_z=Tz/dT1; Tq=dT1; %Характеристики нормальной Земли и нормального поля (межд.асамб.Люцерна, 1967) U=7.2921151467e-5; R=6371000; Om=U; go=9.780318; bet=0.0053024; bet_1=0.0000059; ge_o=go*(1+bet*(sin(fio*pi/180))^2-bet_1*(sin(2*fio*pi/180))^2); %параметры общеземного эллипсоида a=6378160; % большая полуось al=1/298.26;% сжатие b=a*(1-al); e2=(a^2-b^2)/a^2; % квадрат эксцентриситета %Координаты точки старта fio=59.9583; lambdao=30; ho=0; Vo=0; %kurs=0; Roo=359.999*pi/180; Ko=-0.5*pi/180; Psio=0; Tetao=0; %kurs=-60; %Roo=107.9434*pi/180; %Ko=(-0.5+300)*pi/180; %kurs=-120; %Roo=358.4676*pi/180; %Ko=(-0.5+240)*pi/180; %kurs=-180; %Roo=234.285*pi/180; %Ko=(-0.5+180)*pi/180; %kurs=-240; %Roo=140.6186*pi/180; %Ko=(-0.5+120)*pi/180; %kurs=-300; %Roo=242.5121*pi/180; %Ko=(-0.5+60)*pi/180; OmEo=-Vo*cos(Ko)/R; OmNo=U*cos(fio*pi/180)+(Vo*sin(Ko))/R; OmHo=U*sin(fio*pi/180)+(Vo*sin(Ko)/R)*tan(fio*pi/180); Omho=[OmEo;OmNo;OmHo]; % Model GPS po cursu Sigma1DKs=60*5e-6; MUDKs=1/1800; Sigma2DKs=180*5e-6; % Model Laga SigmaVTE=0.2; MUVTE=1/5400; SigmaVTN=0.3; MUVTN=1/5400; % Model shumov Z SigmaZDVEGPS=0.1; SigmaZDVNGPS=0.1; SigmaZDVHGPS=0.1; SigmaZDFiGPS=10/R; SigmaZDLamGPS=10/(R*cos(fio*pi/180)); sigmaH=1; tosrr=1; DDVE=SigmaZDVEGPS^2*tosrr/Tz; DDVN=SigmaZDVNGPS^2*tosrr/Tz; DDVH=SigmaZDVHGPS^2*tosrr/Tz; DDFi=SigmaZDFiGPS^2*tosrr/Tz; DDLam=SigmaZDLamGPS^2*tosrr/Tz; DDh2=sigmaH^2*tosrr/Tz; DDKs=Sigma2DKs^2*tosrr/Tz; SigmaZDVEL=0.3; SigmaZDVNL=0.3; tosrL=1; DDVEL=SigmaZDVEL^2*tosrL/Tz; DDVNL=SigmaZDVNL^2*tosrL/ Tz; % начальные погрешности БИИМ (t=0) Alphao=1*pi/180; Betao=0.3*pi/180; Gammao=-0.3*pi/180; DVEo=1; DVNo=-1; DVHo=1; DFio=50*5e-6/30; DLamo=-50*5e-6/30; Dho=1; X9o=[Alphao;Betao;Gammao;DVEo;DVNo;DVHo;DFio;DLamo;Dho]; VTEo=SigmaVTE; VTNo=-SigmaVTN; KO_prib=Ko+Alphao-tan(Psio)*(Betao*sin(Ko)+Gammao*cos(Ko)); PsiO_prib=Psio-Betao*cos(Ko)+Gammao*sin(Ko); TetaO_prib=Tetao-(Betao*sin(Ko)+Gammao*cos(Ko))/cos(Psio); c11=cos(KO_prib)*cos(TetaO_prib)+sin(KO_prib)*sin(PsiO_prib)*sin(TetaO_prib); c12=sin(KO_prib)*cos(PsiO_prib); c13=cos(KO_prib)*sin(TetaO_prib)-sin(KO_prib)*sin(PsiO_prib)*cos(TetaO_prib); c21=-sin(KO_prib)*cos(TetaO_prib)+cos(KO_prib)*sin(PsiO_prib)*sin(TetaO_prib); c22=cos(KO_prib)*cos(PsiO_prib); c23=-(sin(KO_prib)*sin(TetaO_prib)+cos(KO_prib)*sin(PsiO_prib)*cos(TetaO_prib)); c31=-cos(PsiO_prib)*sin(TetaO_prib); c32=sin(PsiO_prib); c33=cos(PsiO_prib)*cos(TetaO_prib); Coh_o=[c11 c12 c13 C21 c22 c23 c31 c32 c33]; Cbo_o=[cos(Roo),-sin(Roo),0 Sin(Roo),cos(Roo), 0 0, 0, 1]; Cbh_o=Coh_o*Cbo_o; L0=cos(KO_prib/2)*cos(PsiO_prib/2)*cos(TetaO_prib/2)+sin(KO_prib/2)*sin(PsiO_prib/2)*sin(TetaO_prib/2); L1=cos(KO_prib/2)*cos(TetaO_prib/2)*sin(PsiO_prib/2)+sin(KO_prib/2)*sin(TetaO_prib/2)*cos(PsiO_prib/2); L2=cos(KO_prib/2)*sin(TetaO_prib/2)*cos(PsiO_prib/2)-sin(KO_prib/2)*cos(TetaO_prib/2)*sin(PsiO_prib/2); L3=cos(KO_prib/2)*sin(TetaO_prib/2)*sin(PsiO_prib/2)-sin(KO_prib/2)*cos(TetaO_prib/2)*cos(PsiO_prib/2); Lho_o=[L0;L1;L2;L3]; LL=[L0,-L1,-L2,-L3; L1, L0,-L3, L2; L2, L3, L0,-L1; L3,-L2, L1, L0]; Lob_o=[cos(Roo/2); 0; 0; sin(Roo/2)]; Lhb_o=LL*Lob_o; VE0_prib=Vo*sin(Ko)+DVEo; VN0_prib=Vo*cos(Ko)+DVNo; VH0_prib=DVHo; FiO_prib=fio*pi/180+DFio; Lam0_prib=lambdao*pi/180+DLamo; h0_prib=ho+Dho; dV=0; AB=0; G=[0;0;-ge_o]; vekn_htO=dV+AB-G; vekn_btO=(Cbh_o)'*vekn_htO; Ombo=(Cbh_o)'*Omho; % коэффициенты моделей аселерометров и гироскопов DAxo=0; DAyo=0; DAzo=0; DGxo=0*5e-6; DGyo=0*5e-6; DGzo=0*-4.4*5e-6; DMgxo=0; DMgyo=0; DMgzo=0*5e-4; Axo=0*0.12*5e-6; Bxo=0*-0.05*5e-6; Ayo=0*0.08*5e-6; Byo=0*0.02*5e-6; % веса weight_a=1; weight_b=1; weight_DV=1; weight_DFi=1; weight_DLa=1; weight_Dh=1; weight_Drx=1;
weight_Dry=1; weight_Drz=1; weight_Dnx=1; weight_Dny=1; weight_Dnz=1; weight_DMgx=1; weight_DMgy=1; weight_DMgz=1; weight_Rdr=1; weight_DVT=1;
% фильтр Калмана(n=24) % Po SigmaAlphao=0.3*pi/180; SigmaBetao=0.1*pi/180; SigmaGammao=0.1*pi/180; SigmaDVEo=0.3; SigmaDVNo=0.3; SigmaDVHo=0.3; SigmaDFio=10/R; SigmaDLamo=10/(R*cos(fio*pi/180)); SigmaDho=1; SigmaCDXbo=0.3*5e-6; SigmaCDYbo=0.3*5e-6; SigmaCDZbo=0.3*5e-6; SigmaCAksXbo=0.01; SigmaCAksYbo=0.01; SigmaCAksZbo=0.01; SigmaCMgXbo=1e-4; SigmaCMgYbo=1e-4; SigmaCMgZbo=1e-4; SigmaRxAo=0.03*5e-6; SigmaRxBo=0.03*5e-6; SigmaRyAo=0.03*5e-6; SigmaRyBo=0.03*5e-6; SigmaVTEoL=0.2; SigmaVTNoL=0.2; SigmaVTEogps=1e-25*0.1; SigmaVTNogps=1e-25*0.1; po24gps=[SigmaAlphao^2;SigmaBetao^2;SigmaGammao^2; SigmaDVEo^2;SigmaDVNo^2;SigmaDVHo^2; SigmaDFio^2;SigmaDLamo^2;SigmaDho^2; SigmaCDXbo^2;SigmaCDYbo^2;SigmaCDZbo^2; SigmaCAksXbo^2;SigmaCAksYbo^2;SigmaCAksZbo^2; SigmaCMgXbo^2;SigmaCMgYbo^2;SigmaCMgZbo^2; SigmaRxAo^2;SigmaRxBo^2;SigmaRyAo^2;SigmaRyBo^2; SigmaVTEogps^2;SigmaVTNogps^2]; Po24gps=diag(po24gps); % Q SigmaDrE=3*5e-6; SigmaDrN=3*5e-6; SigmaDrH=3*5e-6; SigmaAksE=0.03; SigmaAksN=0.03; SigmaAksH=0.03; SigmaDrFi=5/R; SigmaDrLam=5/(R*cos(fio*pi/180)); SigmaDrh=0.1; SigmadCDrXb=1e-2*0.3*5e-6; SigmadCDrYb=1e-2*0.3*5e-6; SigmadCDrZb=1e-2*0.3*5e-6; SigmadCAksXb=1e-2*0.01; SigmadCAksYb=1e-2*0.01; SigmadCAksZb=1e-2*0.01; SigmadCMgXb=1e-2*1e-4; SigmadCMgYb=1e-2*1e-4; SigmadCMgZb=1e-2*1e-4; SigmadRxA=1e-2*0.03*5e-6; SigmadRxB=1e-2*0.03*5e-6; SigmadRyA=1e-2*0.03*5e-6; SigmadRyB=1e-2*0.03*5e-6; SigmaVTEgps=0; SigmaVTNgps=0; SigmaVTEr=0.2; SigmaVTNr=0.2; MUVTEr=1/5400; MUVTNr=1/5400; q24gps=[SigmaDrH^2;SigmaDrE^2;SigmaDrN^2; SigmaAksE^2;SigmaAksN^2;SigmaAksH^2; SigmaDrFi^2;SigmaDrLam^2;SigmaDrh^2; SigmadCDrXb^2;SigmadCDrYb^2;SigmadCDrZb^2; SigmadCAksXb^2;SigmadCAksYb^2;SigmadCAksZb^2; SigmadCMgXb^2;SigmadCMgYb^2;SigmadCMgZb^2; SigmadRxA^2;SigmadRxB^2;SigmadRyA^2;SigmadRyB^2; 2*MUVTEr*SigmaVTEgps^2/Tq;2*MUVTNr*SigmaVTNgps^2/Tq]; Q24gps=diag(q24gps); q24gpsL=[SigmaDrH^2;SigmaDrE^2;SigmaDrN^2; SigmaAksE^2;SigmaAksN^2;SigmaAksH^2; SigmaDrFi^2;SigmaDrLam^2;SigmaDrh^2; SigmadCDrXb^2;SigmadCDrYb^2;SigmadCDrZb^2; SigmadCAksXb^2;SigmadCAksYb^2;SigmadCAksZb^2; SigmadCMgXb^2;SigmadCMgYb^2;SigmadCMgZb^2; SigmadRxA^2;SigmadRxB^2;SigmadRyA^2;SigmadRyB^2; 2*MUVTEr*SigmaVTEr^2/Tq;2*MUVTNr*SigmaVTNr^2/Tq]; Q24gpsL=diag(q24gpsL); % расчетная модель шумов измерений SigmaDVEGPS=0.3; SigmaDVNGPS=0.3; SigmaDFiGPS=30/R; SigmaDLamGPS=30/(R*cos(fio*pi/180)); SigmaDh=3; SigmaDKs=180*5e-6; SigmaDVEL=0.3; SigmaDVNL=0.3;
H_8_24_gps=[0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; H_8_24_gpsK=[0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; H_8_24N_gpsL=[0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]; H_8_24N_L=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]; r8_mrkL=[SigmaDVEGPS^2;SigmaDVNGPS^2;SigmaDFiGPS^2;SigmaDLamGPS^2; SigmaDh^2;SigmaDKs^2;SigmaDVEL^2;SigmaDVNL^2]; R8A_mrkL=diag(r8_mrkL); % X^o AlphaFKo=0*5e-6; BetaFKo=0*5e-6; GammaFKo=0*5e-6; DVEFKo=0; DVNFKo=0; DVHFKo=0; DFiFKo=0/R; DLamFKo=0/(R*cos(fio*pi/180)); DhFKo=0; ConstgyroXFKo=0*5e-6; ConstgyroYFKo=0*5e-6; ConstgyroZFKo=0*5e-6; ConstAksXFKo=0*5e-5; ConstAksYFKo=0*5e-5; ConstAksZFKo=0*5e-5; ConstMgxFKo=0; ConstMgyFKo=0; ConstMgzFKo=0; RxAFKo=0*5e-6; RxBFKo=0*5e-6; RyAFKo=0*5e-6; RyBFKo=0*5e-6; VTEFKo=0; VTNFKo=0; X24FKo=[AlphaFKo;BetaFKo;GammaFKo; DVEFKo;DVNFKo;DVHFKo; DFiFKo;DLamFKo;DhFKo; ConstgyroXFKo;ConstgyroYFKo;ConstgyroZFKo; ConstAksXFKo;ConstAksYFKo;ConstAksZFKo; ConstMgxFKo;ConstMgyFKo;ConstMgzFKo; RxAFKo;RxBFKo;RyAFKo;RyBFKo; VTEFKo;VTNFKo];
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.217.1 (0.012 с.) |

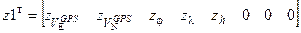 .
.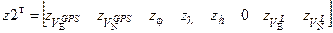 .
.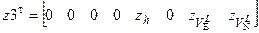 .
. ключи №1 и 2 позволяют выбрать источник информации о курсе (либо приборное значение курса K, либо гирокомпас K_gk, либо МРК K_gmrk);
ключи №1 и 2 позволяют выбрать источник информации о курсе (либо приборное значение курса K, либо гирокомпас K_gk, либо МРК K_gmrk);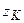 (в работе курсовое измерение использоваться не будет);
(в работе курсовое измерение использоваться не будет);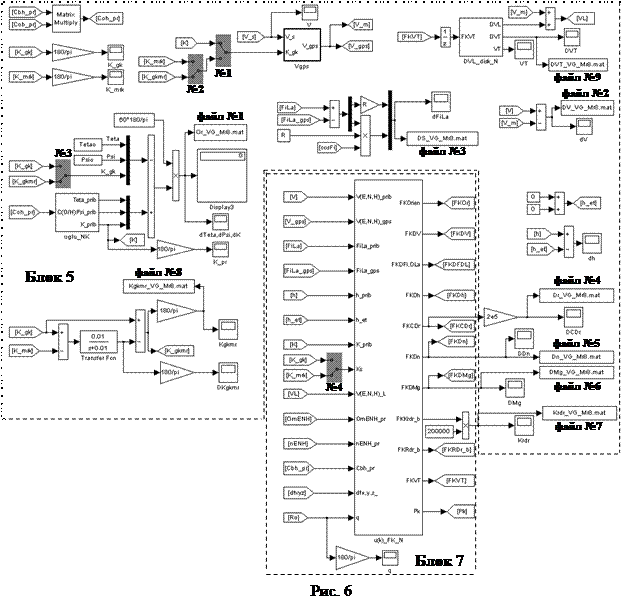
 ) и скоростных (
) и скоростных ( ) измерений
) измерений
 находится на «Панели задач»), в окне «Current Directory» указать путь к рабочей папке d:\student\Emlib\Prog_Lab_EP \ (в ней размещены file Matlab: loader_Ncn.m, IS24re_VG_MrRdr_dat03_04p1.m, M_IS24re_VG_MrRdr_Lit_f.mdl, 2_Mr4.mat и запустить Matlab);
находится на «Панели задач»), в окне «Current Directory» указать путь к рабочей папке d:\student\Emlib\Prog_Lab_EP \ (в ней размещены file Matlab: loader_Ncn.m, IS24re_VG_MrRdr_dat03_04p1.m, M_IS24re_VG_MrRdr_Lit_f.mdl, 2_Mr4.mat и запустить Matlab); ) и задать 4-х часовой массив данных (n = 1440000).
) и задать 4-х часовой массив данных (n = 1440000).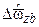 ,
,  и
и 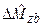 ):
): ). Открыть файл M_IS24re_VG_MrRdr_Lit_f.mdl ( для этого на панели инструментов Simulink Library Browser нажать
). Открыть файл M_IS24re_VG_MrRdr_Lit_f.mdl ( для этого на панели инструментов Simulink Library Browser нажать  на панели инструментов ).
на панели инструментов ).


